Ph.D. thesis (pdf) - dirac

82 Alpha Relaxation
2
1
0
216.4K this work
Patm Mandanici 05
log 10
τ α
[s]
−1
−2
−3
−4
−5
−6
log 10
(τ α
) [s]
2
0
−2
−4
−6
−7
0 100 200 300
P [MPa]
−8
1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18 1.2
ρ [g/cm 3 ]
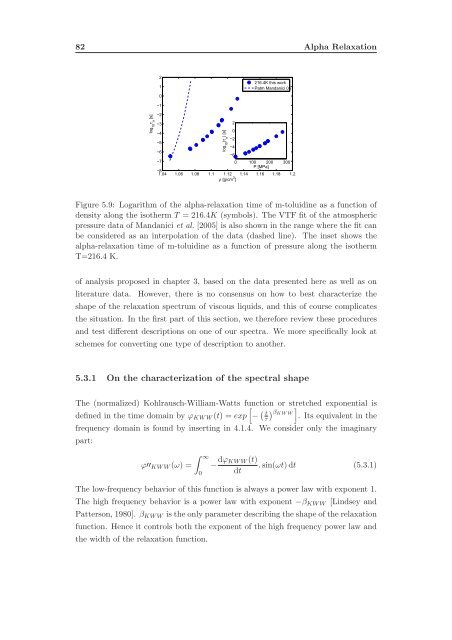
Figure 5.9: Logarithm of the alpha-relaxation time of m-toluidine as a function of
density along the isotherm T = 216.4K (symbols). The VTF fit of the atmospheric
pressure data of Mandanici et al. [2005] is also shown in the range where the fit can
be considered as an interpolation of the data (dashed line). The inset shows the
alpha-relaxation time of m-toluidine as a function of pressure along the isotherm
T=216.4 K.
of analysis proposed in chapter 3, based on the data presented here as well as on
literature data. However, there is no consensus on how to best characterize the
shape of the relaxation spectrum of viscous liquids, and this of course complicates
the situation. In the first part of this section, we therefore review these procedures
and test different descriptions on one of our spectra. We more specifically look at
schemes for converting one type of description to another.
5.3.1 On the characterization of the spectral shape
The (normalized) Kohlrausch-William-Watts function [ or stretched exponential is
defined in the time domain by ϕ KWW (t) = exp − ( ) ]
t βKWW
τ
. Its equivalent in the
frequency domain is found by inserting in 4.1.4. We consider only the imaginary
part:
ϕ′′ KWW (ω) =
∫ ∞
0
− dϕ KWW(t)
. sin(ωt)dt (5.3.1)
dt
The low-frequency behavior of this function is always a power law with exponent 1.
The high frequency behavior is a power law with exponent −β KWW [Lindsey and
Patterson, 1980]. β KWW is the only parameter describing the shape of the relaxation
function. Hence it controls both the exponent of the high frequency power law and
the width of the relaxation function.