Introduction to Digital Signal and System Analysis - Tutorsindia

Introduction to Digital Signal and System Analysis
Spectral Analysis by DFT
3
2
1
x[n]
0
-1
-2
-3
0 0.2 0.4 0.6 0.8 1
seconds
600
|X[k]| 400
200
0
0 100 200 300 400 500
Hz
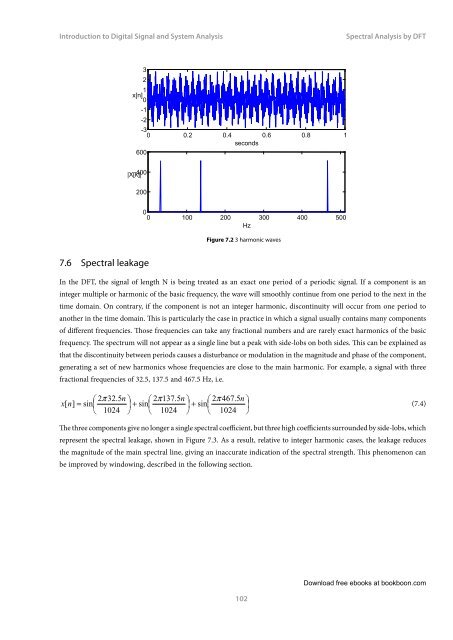
Figure 7.2 3 harmonic waves
7.6 Spectral leakage
In the DFT, the signal of length N is being treated as an exact one period of a periodic signal. If a component is an
integer multiple or harmonic of the basic frequency, the wave will smoothly continue from one period to the next in the
time domain. On contrary, if the component is not an integer harmonic, discontinuity will occur from one period to
another in the time domain. This is particularly the case in practice in which a signal usually contains many components
of different frequencies. Those frequencies can take any fractional numbers and are rarely exact harmonics of the basic
frequency. The spectrum will not appear as a single line but a peak with side-lobs on both sides. This can be explained as
that the discontinuity between periods causes a disturbance or modulation in the magnitude and phase of the component,
generating a set of new harmonics whose frequencies are close to the main harmonic. For example, a signal with three
fractional frequencies of 32.5, 137.5 and 467.5 Hz, i.e.
2π
32.5n
2π
137.5n
2π
467.5n
x[
n]
= sin
+ sin
+ sin
1024 1024 1024
(7.4)
The three components give no longer a single spectral coefficient, but three high coefficients surrounded by side-lobs, which
represent the spectral leakage, shown in Figure 7.3. As a result, relative to integer harmonic cases, the leakage reduces
the magnitude of the main spectral line, giving an inaccurate indication of the spectral strength. This phenomenon can
be improved by windowing, described in the following section.
102
Download free ebooks at bookboon.com