Introduction to Digital Signal and System Analysis - Tutorsindia

Introduction to Digital Signal and System Analysis
Digital Signals and Sampling
1.3 Analogue-to-digital conversion
Although some signals are originally digital, such as population data, number of vehicles and share prices, many practical
signals start off in analogue form. They are continuous signals, such as human’s blood pressure, temperature and heart
pulses. A continuous signal can be first converted to a proportional voltage waveform by a suitable transducer, i.e. the
analogue signal is generated. Then, for adapting digital processor, the signal has to be converted into digital form by
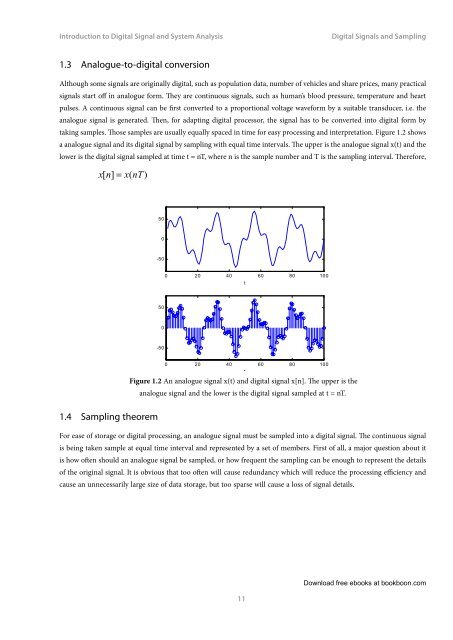
taking samples. Those samples are usually equally spaced in time for easy processing and interpretation. Figure 1.2 shows
a analogue signal and its digital signal by sampling with equal time intervals. The upper is the analogue signal x(t) and the
lower is the digital signal sampled at time t = nT, where n is the sample number and T is the sampling interval. Therefore,
x [ n]
= x(
nT)
50
0
-50
0 20 40 60 80 100
t
50
0
-50
0 20 40 60 80 100
t
Figure 1.2 An analogue signal x(t) and digital signal x[n]. The upper is the
analogue signal and the lower is the digital signal sampled at t = nT.
1.4 Sampling theorem
For ease of storage or digital processing, an analogue signal must be sampled into a digital signal. The continuous signal
is being taken sample at equal time interval and represented by a set of members. First of all, a major question about it
is how often should an analogue signal be sampled, or how frequent the sampling can be enough to represent the details
of the original signal. It is obvious that too often will cause redundancy which will reduce the processing efficiency and
cause an unnecessarily large size of data storage, but too sparse will cause a loss of signal details.
11
Download free ebooks at bookboon.com