Introduction to Digital Signal and System Analysis - Tutorsindia

Introduction to Digital Signal and System Analysis
Time-domain Analysis
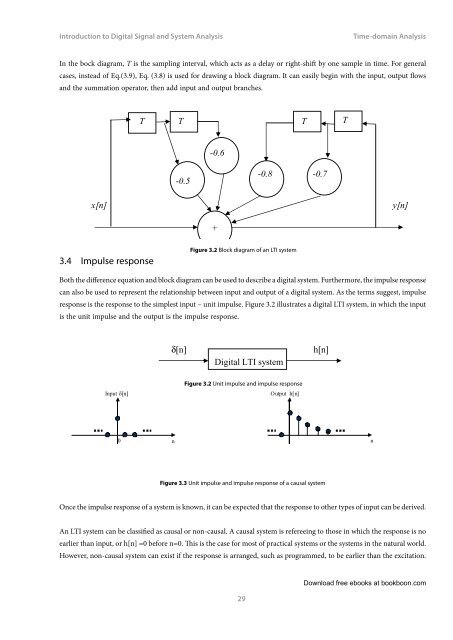
In the bock diagram, T is the sampling interval, which acts as a delay or right-shift by one sample in time. For general
cases, instead of Eq.(3.9), Eq. (3.8) is used for drawing a block diagram. It can easily begin with the input, output flows
and the summation operator, then add input and output branches.
T T T T
-0.6
-0.5
-0.8
-0.7
x[n]
y[n]
+
3.4 Impulse response
Figure 3.2 Block diagram of an LTI system
Both the difference equation and block diagram can be used to describe a digital system. Furthermore, the impulse response
can also be used to represent the relationship between input and output of a digital system. As the terms suggest, impulse
response is the response to the simplest input – unit impulse. Figure 3.2 illustrates a digital LTI system, in which the input
is the unit impulse and the output is the impulse response.
δ[n]
Digital LTI system
h[n]
Input d[n]
Figure 3.2 Unit impulse and impulse response
Output h[n]
0 n n
Figure 3.3 Unit impulse and impulse response of a causal system
Once the impulse response of a system is known, it can be expected that the response to other types of input can be derived.
An LTI system can be classified as causal or non-causal. A causal system is refereeing to those in which the response is no
earlier than input, or h[n] =0 before n=0. This is the case for most of practical systems or the systems in the natural world.
However, non-causal system can exist if the response is arranged, such as programmed, to be earlier than the excitation.
29
Download free ebooks at bookboon.com