Sullivan Microsite DigiSample
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>Sullivan</strong> AP˙<strong>Sullivan</strong>˙Chapter01 October 8, 2016 17:4<br />
<strong>Sullivan</strong><br />
116 Chapter 1 • Limits and Continuity<br />
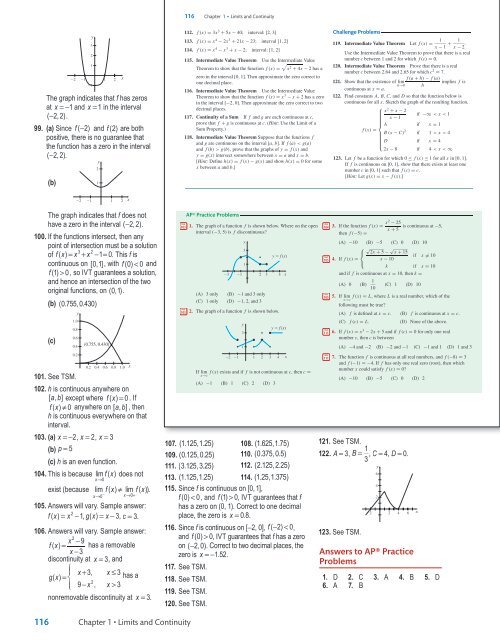
y<br />
3<br />
2<br />
1<br />
22 21<br />
21<br />
1 2<br />
The graph indicates that f has zeros<br />
at x =− 1 and x = 1 in the interval<br />
( −2,2).<br />
99. (a) Since f ( −2) and f (2) are both<br />
positive, there is no guarantee that<br />
the function has a zero in the interval<br />
( −2,2).<br />
(b)<br />
y<br />
2<br />
1<br />
x<br />
112. f (x) = 3x 3 + 5x − 40; interval: [2, 3]<br />
113. f (x) = x 4 − 2x 3 + 21x − 23; interval [1, 2]<br />
114. f (x) = x 4 − x 3 + x − 2; interval: [1, 2]<br />
115. Intermediate Value Theorem Use the Intermediate Value<br />
<br />
Theorem to show that the function f (x) = x 2 + 4x − 2 has a<br />
zero in the interval [0, 1]. Then approximate the zero correct to<br />
one decimal place.<br />
116. Intermediate Value Theorem Use the Intermediate Value<br />
Theorem to show that the function f (x) = x 3 − x + 2 has a zero<br />
in the interval [−2, 0]. Then approximate the zero correct to two<br />
decimal places.<br />
117. Continuity of a Sum If f and g are each continuous at c,<br />
prove that f + g is continuous at c.(Hint: Use the Limit of a<br />
Sum Property.)<br />
118. Intermediate Value Theorem Suppose that the functions f<br />
and g are continuous on the interval [a, b]. If f (a) g(b), prove that the graphs of y = f (x) and<br />
y = g(x) intersect somewhere between x = a and x = b.<br />
[Hint: Define h(x) = f (x) − g(x) and show h(x) = 0 for some<br />
x between a and b.]<br />
Challenge Problems<br />
119. Intermediate Value Theorem Let f (x) = 1<br />
x − 1 + 1<br />
x − 2 .<br />
Use the Intermediate Value Theorem to prove that there is a real<br />
number c between 1 and 2 for which f (c) = 0.<br />
120. Intermediate Value Theorem Prove that there is a real<br />
number c between 2.64 and 2.65 for which c 2 = 7.<br />
f (a + h) − f (a)<br />
121. Show that the existence of lim<br />
implies f is<br />
h→0 h<br />
continuous at x = a.<br />
122. Find constants A, B, C, and D so that the function below is<br />
continuous for all x. Sketch the graph of the resulting function.<br />
⎧<br />
x 2 + x − 2<br />
if −∞ < x < 1<br />
x − 1<br />
⎪⎨ A if x = 1<br />
f (x) =<br />
B (x − C) 2 if 1 < x < 4<br />
D<br />
⎪⎩<br />
if x = 4<br />
2x − 8 if 4 < x < ∞<br />
123. Let f be a function for which 0 ≤ f (x) ≤ 1 for all x in [0, 1].<br />
If f is continuous on [0, 1], show that there exists at least one<br />
number c in [0, 1] such that f (c) = c.<br />
[Hint: Let g(x) = x − f (x).]<br />
2 1 1 2<br />
x<br />
The graph indicates that f does not<br />
have a zero in the interval ( −2,2).<br />
100. If the functions intersect, then any<br />
point of intersection must be a solution<br />
3 2<br />
of fx ( ) = x + x − 1=<br />
0. This f is<br />
continuous on [0,1] , with f (0) < 0 and<br />
f (1) > 0, so IVT guarantees a solution,<br />
and hence an intersection of the two<br />
original functions, on (0,1).<br />
(b) (0.755,0.430)<br />
(c)<br />
y<br />
1.0<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
101. See TSM.<br />
(0.755, 0.430)<br />
0.2 0.4 0.6 0.8 1.0<br />
102. h is continuous anywhere on<br />
[ ab , ] except where fx ( ) = 0 . If<br />
fx ( ) ≠ 0 anywhere on [ ab , ] , then<br />
h is continuous everywhere on that<br />
interval.<br />
103. (a) x =− 2, x = 2, x = 3<br />
(b) p = 5<br />
(c) h is an even function.<br />
104. This is because lim fx ( ) does not<br />
x → 0<br />
exist (because lim fx ( ) ≠ lim fx ( )).<br />
−<br />
x→0 x→+<br />
0<br />
105. Answers will vary. Sample answer:<br />
fx ( ) = x<br />
2 −1,<br />
gx ( ) = x − 3, c = 3.<br />
106. Answers will vary. Sample answer:<br />
2<br />
x −9<br />
fx ( ) = has a removable<br />
x −3<br />
discontinuity at x = 3, and<br />
⎧<br />
⎪ x+ 3, x≤3<br />
gx ( ) = ⎨<br />
has a<br />
2<br />
⎩⎪ 9 − x , x><br />
3<br />
nonremovable discontinuity at x = 3.<br />
x<br />
AP® Practice Problems<br />
PAGE<br />
103 1. The graph of a function f is shown below. Where on the open<br />
interval (−3, 5) is f discontinuous?<br />
23<br />
21<br />
(A) 3 only (B) −1 and 3 only<br />
(C) 1 only (D) −1, 2, and 3<br />
y<br />
3<br />
1<br />
y 5 f (x)<br />
2 3 5 x<br />
PAGE<br />
103 2. The graph of a function f is shown below.<br />
22 21<br />
y<br />
3<br />
1<br />
y 5 f (x)<br />
1 2 3 4<br />
If lim x→c<br />
f (x) exists and if f is not continuous at c, then c =<br />
(A) −1 (B) 1 (C) 2 (D) 3<br />
107. (1.125,1.25) 108. (1.625,1.75)<br />
109. (0.125,0.25) 110. (0.375,0.5)<br />
111. (3.125,3.25) 112. (2.125,2.25)<br />
113. (1.125,1.25) 114. (1.25,1.375)<br />
115. Since f is continuous on [0, 1],<br />
f (0) < 0, and f (1) > 0, IVT guarantees that f<br />
has a zero on (0, 1). Correct to one decimal<br />
place, the zero is x = 0.8.<br />
116. Since f is continuous on [−2, 0], f ( − 2) < 0,<br />
and f (0) > 0, IVT guarantees that f has a zero<br />
on ( −2,0). Correct to two decimal places, the<br />
zero is x =− 1.52.<br />
117. See TSM.<br />
118. See TSM.<br />
119. See TSM.<br />
120. See TSM.<br />
x<br />
PAGE<br />
104 3. If the function f (x) = x2 − 25<br />
then f (−5) =<br />
x + 5<br />
is continuous at −5,<br />
(A) −10 (B) −5 (C) 0 (D) 10<br />
⎧ √ √<br />
⎨ 2x + 5 − x + 15<br />
if x = 10<br />
PAGE<br />
105 4. If f (x) = x − 10<br />
⎩<br />
k if x = 10<br />
and if f is continuous at x = 10, then k =<br />
1<br />
(A) 0 (B) (C) 1 (D) 10<br />
10<br />
PAGE<br />
105 5. If lim f (x) = L, where L is a real number, which of the<br />
x→c<br />
following must be true?<br />
(A) f is defined at x = c. (B) f is continuous at x = c.<br />
(C) f (c) = L. (D) None of the above.<br />
PAGE<br />
111 6. If f (x) = x 3 − 2x + 5 and if f (c) = 0 for only one real<br />
number c, then c is between<br />
(A) −4 and −2 (B) −2 and −1 (C) −1 and 1 (D) 1 and 3<br />
PAGE<br />
111 7. The function f is continuous at all real numbers, and f (−8) = 3<br />
and f (−1) =−4. If f has only one real zero (root), then which<br />
number x could satisfy f (x) = 0?<br />
(A) −10 (B) −5 (C) 0 (D) 2<br />
121. See TSM.<br />
122. A = 3, B = 1 , C = 4, D = 0.<br />
3<br />
123. See TSM.<br />
y<br />
6<br />
4<br />
2<br />
22 2 4 6<br />
Answers to AP® Practice<br />
Problems<br />
1. D 2. C 3. A 4. B 5. D<br />
6. A 7. B<br />
x<br />
116<br />
Chapter 1 • Limits and Continuity<br />
TE_<strong>Sullivan</strong>_Chapter01_PART I.indd 13<br />
11/01/17 9:58 am