Sullivan Microsite DigiSample

Sullivan AP˙Sullivan˙Chapter01 October 8, 2016 17:4
Section 1.5 • Infinite Limits; Limits at Infinity; Asymptotes 131
y
x c
y f (x)
c x
(a) lim f(x) ∞
x→c
Figure 53
y
y f (x)
x c
c
x
(b) lim f(x) ∞
x→c
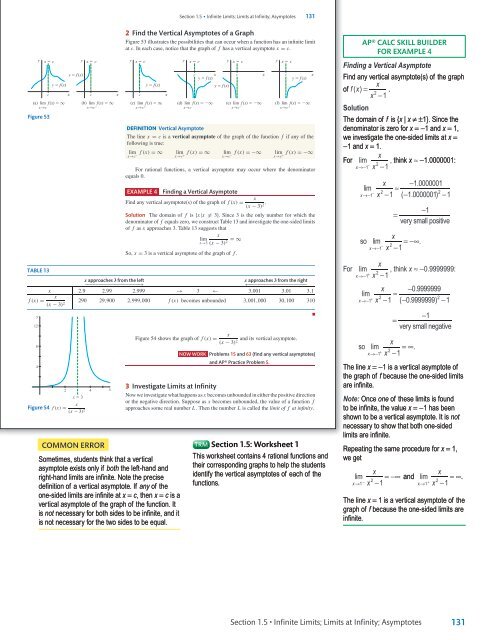
2 Find the Vertical Asymptotes of a Graph
Figure 53 illustrates the possibilities that can occur when a function has an infinite limit
at c. In each case, notice that the graph of f has a vertical asymptote x = c.
y
x c
y f (x)
c
x
(c) lim f(x) ∞
x→c
lim
x→c
y
x c y x c y x c
c x
c x
c
y f (x)
y f (x)
(d) lim f(x) ∞
x→c
x→c
x→c
(e) lim f(x) ∞
x→c
y f (x)
(f) lim f(x) ∞
x→c
DEFINITION Vertical Asymptote
The line x = c is a vertical asymptote of the graph of the function f if any of the
following is true:
f (x) =∞ lim f (x) =∞ lim f (x) = −∞ lim f (x) = −∞
− + −
x→c +
For rational functions, a vertical asymptote may occur where the denominator
equals 0.
EXAMPLE 4 Finding a Vertical Asymptote
x
Find any vertical asymptote(s) of the graph of f (x) =
(x − 3) . 2
Solution The domain of f is {x|x = 3}. Since 3 is the only number for which the
denominator of f equals zero, we construct Table 13 and investigate the one-sided limits
of f as x approaches 3. Table 13 suggests that
x
lim
x→3 (x − 3) =∞ 2
So, x = 3 is a vertical asymptote of the graph of f .
x
AP® CaLC skill builder
for example 4
Finding a Vertical Asymptote
Find any vertical asymptote(s) of the graph
x
of fx ( ) = .
2
x −1
Solution
The domain of f is {x | x ≠ ±1}. Since the
denominator is zero for x = −1 and x = 1,
we investigate the one-sided limits at x =
−1 and x = 1.
For lim , think x ≈ −1.0000001:
x→−1
x−
− 2
x 1
x
− ≈ −1.0000001
lim
2 2
x 1 ( −1.0000001) −1
−
x→−1
−1
=
very small positive
x
so lim
− =−∞ .
− 2
x→−1
x 1
TABLE 13
x approaches 3 from the left
x approaches 3 from the right
−−−−−−−−−−−−−−−−−−→
←−−−−−−−−−−−−−−−−−−−
x 2.9 2.99 2.999 → 3 ← 3.001 3.01 3.1
x
f (x) =
290 29,900 2,999,000 f (x) becomes unbounded 3,001,000 30,100 310
(x − 3) 2
y
12
8
4
Figure 54 shows the graph of f (x) =
x
and its vertical asymptote.
(x − 3)
2
NOW WORK Problems 15 and 63 (find any vertical asymptotes)
and AP® Practice Problem 5.
x
3 Investigate Limits at Infinity
2
4
x 3
Now we investigate what happens as x becomes unbounded in either the positive direction
or the negative direction. Suppose as x becomes unbounded, the value of a function f
x
Figure 54 f (x) =
approaches some real number L. Then the number L is called the limit of f at infinity.
(x − 3) 2
common error
Sometimes, students think that a vertical
asymptote exists only if both the left-hand and
right-hand limits are infinite. Note the precise
definition of a vertical asymptote. If any of the
one-sided limits are infinite at x = c, then x = c is a
vertical asymptote of the graph of the function. It
is not necessary for both sides to be infinite, and it
is not necessary for the two sides to be equal.
TRM Section 1.5: Worksheet 1
This worksheet contains 4 rational functions and
their corresponding graphs to help the students
identify the vertical asymptotes of each of the
functions.
■
For
lim , think x ≈ −0.9999999:
2
x 1
x
− ≈ −0.9999999
lim
+ 2 2
x→−1
x 1 ( −0.9999999) −1
x→− 1
x−
+
−1
=
very small negative
x
so lim
− =∞ .
+ 2
x→−1
x 1
The line x = −1 is a vertical asymptote of
the graph of f because the one-sided limits
are infinite.
Note: Once one of these limits is found
to be infinite, the value x = −1 has been
shown to be a vertical asymptote. It is not
necessary to show that both one-sided
limits are infinite.
Repeating the same procedure for x = 1,
we get
x
lim
x − 1
=−∞ and lim
2
x→1
−
x→ 1
+
x
x − 1
=∞ .
2
The line x = 1 is a vertical asymptote of the
graph of f because the one-sided limits are
infinite.
Section 1.5 • Infinite Limits; Limits at Infinity; Asymptotes
131
TE_Sullivan_Chapter01_PART II.indd 14
11/01/17 9:55 am