Sullivan Microsite DigiSample

Sullivan AP˙Sullivan˙Chapter01 October8, 8, 2016 17:4
Section 1.1 • Limits of Functions Using Section Numerical 1.1 • Assess and Graphical Your Understanding Techniques 89 79
(b) Investigate lim cos π by using a table and evaluating In planethe
geometry, a tangent (c) Graph linethe tofunction a circleC.
is defined as a line having exactly one
x→0 x2 function f (x) = cos π point in common with the circle, as shown in Figure 3. However, this definition does
x 2 at
(d) Use the graph to investigate lim C(w) and lim C(w). Do
not work for graphs in general. For example, in Figure 4, w→1 the − three lines w→1 1 + , 2 , and 3
x =− 2 3 , − 2 5 , − 2 7 , − 2 9 ,..., 2 9 , 2 7 , 2 5 , 2 contain the point P and have exactly these suggest one point thatinlimcommon C(w) exists? with the graph of f , but they
3 .
w→1
P
do not meet the requirement of just touching the graph at P. On the other hand,
(e) Use the graph to investigate lim C(w) and lim C(w). the line
T just touches the graph of f at P, but it intersects thew→12 graph − at other points. w→12
(c) Compare the results from (a) and (b). What do you conclude
+ It is the
slope of the tangent line
about the limit? Why do you think this happens? What is your T that Do distinguishes these suggestithat fromlimallC(w) otherexists?
lines containing P.
w→12
Figure 3 Tangent line to a circle at the
view about using a table to draw a conclusion about So before limits? defining a tangent (f) Use line, thewe graph investigate to investigate its slope, lim which C(w). we denote by m
point P.
tan .
w→0
We begin with the graph of a function f , a point P on its graph, +
(d) Use technology to graph f . Begin with the x-window
(g) Use the graph to investigate lim C(w). and the tangent line T
to f at P, as shown in Figure 5.
w→13
[−2π, 2π] and the y-window [−1, 1]. If you were finding
− y
lim f (x) l using l a graph, what would you conclude? Zoom in
2 1
The tangent line T 61. to Correlating the graph ofStudent f at P Success must contain to Study theTime point P. Professor We denote Smiththe
x→0l y f (x)
3
on the graph. Describe what you see. (Hint:
coordinates
Be sure your
of P by (c, f (c)). claims Since that afinding student’s a final slopexam requires score two is a function points, of and thewe time have t
calculator is set to the radian mode.) only one point on the tangent (in hours) line T that , wethe proceed studentas studies. follows. He claims that the closer to
PAGE
x −l 8 T
85 57. (a) Use a table to investigate lim .
Suppose we choose any seven point hours Q one = studies, (x, f (x)), the closer othertothan 100% P, the onstudent the graph scoresof f ,
x→2 2
on the final. He claims that studying significantly less than seven
Tangent as shown in Figure 6. (Q can be to the left or to the right of P; we chose Q to be to the
(b) How close must x be to 2, soline
that f (x) is within 0.1 of the hours may cause one to be underprepared for the test, while
limit?
right of P.) The line containing studying thesignificantly points P = more (c, f than (c)) seven and Q hours = (x, mayf cause (x)) is called a
P
secant line of the graph of
(c) How close must x be to 2, so that f (x) is within 0.01 of the “burnout.” f . The slope m sec of this secant line is
limit?
(a) Write Professor f (x) Smith’s − f (c)
m claim symbolically as a limit.
sec = (1)
58. (a) Use a table to investigate lim(5 − 2x). x
x→2 (b) Write Professorx Smith’s − c claim using the ε-δ definition
(b) How close must x be to 2, so that f (x) is within 0.1 of the
of limit.
Figure 4
Figure 7 shows three different points Q 1 , Q 2 , and Q 3 on the graph of f that are
limit?
successively closer to pointSource: P, andSubmitted three associated by the students secantof lines Millikin 1 , University.
2 , and 3 . The closer
(c) How close must x be to 2, so that f (x) isthe within point 0.01 Q is ofto the the point 62. P, The thedefinition closer theofsecant the slope lineof isthe to the tangent tangent line line to the T graph . Theof
line T ,
limit?
the limiting position of these secant lines, is the tangent line to the graph
f (x)
of
− f
(c)
at P.
59. First-Class Mail As of April
y = f (x) at the point (c, f (c)) is m tan = lim
.
y
y
y
x→c
2016, the U.S. Postal Service
x − c
y f (x)
y f (x)
charged $0.47 postage for
Another Secant
y f (x)
way to express this slope is to define a new variable l 1 Secant
first-class letters weighing up to
h = x
line
l2l3 lines
Q (x, f (x)) − c. Rewrite the slope of the tangent line m tan Q 1
using h and c.
and including 1 ounce, plus a flat
63. If f (2) = 6, can you conclude anything about lim f (x)? Explain
fee of $0.21 for each additional l x→2
T
your reasoning.
l Q T
2 l T
Q
or partial ounce up to and
3
Tangent
64. If limTangent
f (x) = 6, can you conclude anything about f (2)? Tangent Explain
including P 3.5 (c, f ounces. (c)) First-class
P (c, f (c)) x→2
P (c, f (c))
line
line
line
letter rates do not apply to letters
your reasoning.
weighing more than 3.5 ounces.
65. The graph of f (x) = x − 3 is a straight line with a point punched
Source: U.S. Postal c Service Notice 123 x
c
3 − x
out. x
x
c x x
3 x 2 x 1
x
Figure (a) 5Find m tan
a = function slope of C the thattangent modelsline.
the first-class postage charged,
Figure 6 m sec = slope of a(a) secant What line. straight line and DF what Figure point? 7
in dollars, for a letter weighing w ounces. Assume w>0.
(b) Use the graph of f to investigate the one-sided limits of f as
(b) What is the domain of C?
If the limiting position of xthe approaches secant lines 3. is the tangent line, then the limit of the
(c) Graph the function C.
slopes of the secant lines should (c) Does equal the graph the slope suggest of the thattangent lim f (x) exists? If so, what is it?
(d) Use the graph to investigate lim C(w) and lim C(w). Do
x→3
line. Notice in Figure 7
w→2− thatw→2 as + the point Q moves closer to the point P, the numbers x get closer to c. So,
66. (a) Use a table to investigate lim(1 + x)
these suggest that lim C(w) exists? equation (1) suggests that
1/x .
x→0
w→2
(e) Use the graph to investigate lim C(w).
m (b) Use graphing technology to graph g(x) = (1 + x) 1/x tan = [Slope of the tangent line to f at P]
.
[
]
Tangent line at P w→0 + (c) What f do (x) (a) −and f (c) (b) suggest about lim(1 + x) 1/x ?
(f) Use the graph to investigate lim C(w).
= Limit of
as x gets closer x→0 to c
w→3.5 − x − c
CAS (d) Find lim(1 + x) 1/x .
x→0
60. First-Class Mail As of April 2016, the U.S. InPostal symbols, Service we write
P
f (x) − f (c)
charged $0.94 postage for first-class large envelope weighing up to
m tan = lim
and including 1 ounce, plus a flat fee of $0.21 for each additional
x→c x − c
or partial ounce up to and including 13 ounces. The First-class notation rates limdois read, Challenge “the limit Problems as x approaches c.”
x→c
not apply to large envelopes weighing more than 13 ounces.
The tangent line to Forthe Problems graph of 67–70, a function investigate f at each a point of theP following = (c, f limits. (c)) is the line
Source: U.S. Postal Service Notice 123
{
containing the point P whose slope is
1 if x is an integer
Kathryn Sidenstricker /Dreamstime.com
f (x) =
(a) Find a function C that models the first-class postage charged,
f (x) − f (c)
in dollars, for a large envelope weighing w ounces. Assume
m tan = lim
w>0.
67. lim f (x) x→c 68. limx −f (x) c 69. lim
x→2 x→1/2 x→3
(b) What is the domain ofSecant
C?
provided the limit exists.
Figure 8
lines
WEB SITE
Mathscoop: The Mathscoop Web site has a
secant and tangent line applet that you may want
to demo in class. You can drag one point of the
secant line to the point of tangency to show the
relationship between the two lines. The applet
allows you to click Play to show the animation
to the students. This can help to show how x
approaches c when demonstrating how the slope
of the secant line approaches that of the tangent
line. A link to this resource is available on the
Additional Chapter 1 Resources document,
available for download.
0 if x is not an integer
f (x) 70. lim
x→0 f (x)
As Figure 8 illustrates, this new idea of a tangent line is consistent with the traditional
definition of a tangent line to a circle.
Teaching Tip
Students should be familiar with finding the slope
of a line given two points. When those two points
fall on the graph of a function, we call the line that
connects them the secant line. The word “secant”
comes from the Latin word secare, meaning to
cut. As the two points that create the secant line
become closer and closer together on the curve,
the slope of the secant line approaches the slope
of the tangent line to the point upon which they are
converging.
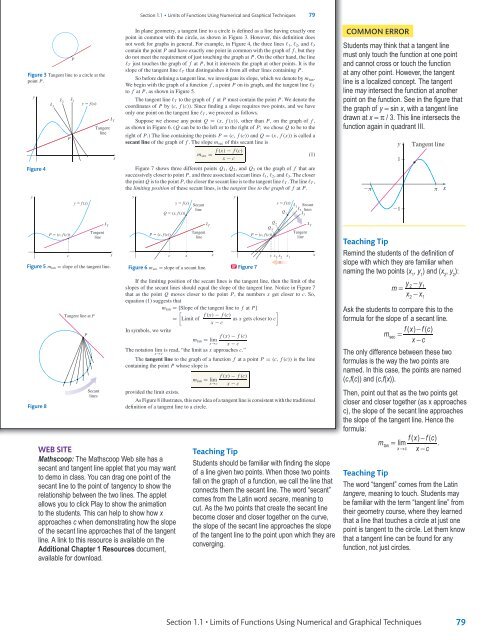
common error
Students may think that a tangent line
must only touch the function at one point
and cannot cross or touch the function
at any other point. However, the tangent
line is a localized concept. The tangent
line may intersect the function at another
point on the function. See in the figure that
the graph of y = sin x, with a tangent line
drawn at x = π / 3. This line intersects the
function again in quadrant III.
2π
y
1
21
Tangent line
Teaching Tip
Remind the students of the definition of
slope with which they are familiar when
naming the two points (x 1
, y 1
) and (x 2
, y 2
):
m −
=
y y 2 1
x − x
2 1
Ask the students to compare this to the
formula for the slope of a secant line.
fx ( ) − fc ()
msec
=
x−
c
The only difference between these two
formulas is the way the two points are
named. In this case, the points are named
(c,f(c)) and (c,f(x)).
Then, point out that as the two points get
closer and closer together (as x approaches
c), the slope of the secant line approaches
the slope of the tangent line. Hence the
formula:
fx fc
m lim ( ) − ()
x c
.
tan =
x→c
−
Teaching Tip
The word “tangent” comes from the Latin
tangere, meaning to touch. Students may
be familiar with the term “tangent line” from
their geometry course, where they learned
that a line that touches a circle at just one
point is tangent to the circle. Let them know
that a tangent line can be found for any
function, not just circles.
π
x
Section 1.1 • Limits of Functions Using Numerical and Graphical Techniques 79
TE_Sullivan_Chapter01_PART 0.indd 8
11/01/17 9:51 am