Polymers in Confined Geometry.pdf

More documents

Recommendations

Info

18 CHAPTER 2. POLYMER MODELS We will see in the following that the different possible volumes vi can give significantly different results for the relevance of self-avoidance as well as the scaling in a confining tube. In this context the important parameter is the relation of segment length to thickness b/h, called aspect-ratio. Relevance of self-avoidance in static problems In static problems the self-avoidance does not play a role for all flexible polymers 8 : • For a system in θ-condition we can use the ideal chain model. • Whether or not self-avoidance has to be taken into account depends on the number of binary contacts Nφ between the segments. Only if this number is large an effect is to be expected. Therefore there exists a critical number of segments Nc where a cross-over between the description as ideal phantom chain and as self-avoiding chain is expected. This cross-over will be investigated in the following. The scaling relation for the end-to-end distance of a free flexible polymer, eq. (2.6), is valid for a specific range of values of N. But N must not be too small since we still need L ≫ lp. Starting from a specific N ≈ Nc self-avoidance starts playing a role. Using eq. (2.6) a scaling relation for Nc can be derived. The number of binary contacts is given by (using eq. (2.32)) 1/2 v Nφ ∼ N b3 ! = B, (2.37) with an arbitrary constant B > 1. The number of binary contacts should be large for a significant influence of self-avoidance on the conformation. Solving for N yields a scaling relation for the critical number of segments: Nc ∼ b6 . (2.38) v2 For N > Nc self-avoidance is relevant. The N-dependence of R can be split in two regimes with a cross-over point at Nc which is sketched in figure 2.6. As mentioned above the scaling of Nc depends crucially on the average volume occupied by a monomer v. The following three results are obtained for the three 8 For the dynamic properties there is an additional effect of dynamic traps. By ergodicity all configurations are allowed, but some can be very difficult to reach. E.g. when the chain would have to cross through itself these conformations are close in configuration space, but since the segments are impenetrable the polymer would have to uncoil and coil up again to make the conformation change. This difficulty does not occur for static problems!
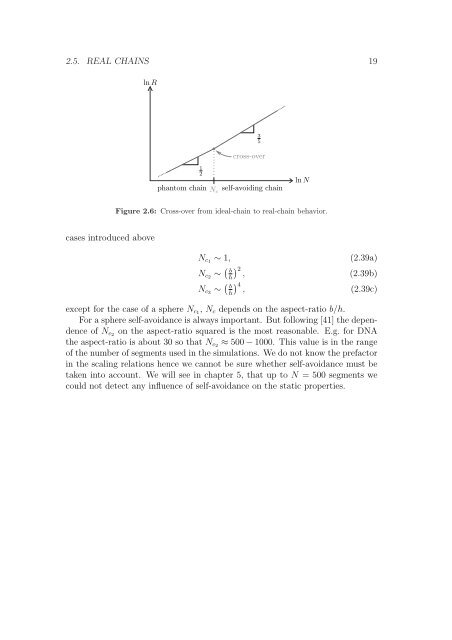
2.5. REAL CHAINS 19 ln R cases introduced above 1 2 phantom chain Nc 3 5 cross-over self-avoiding chain ln N Figure 2.6: Cross-over from ideal-chain to real-chain behavior. Nc1 ∼ 1, (2.39a) Nc2 ∼ b 2 , (2.39b) h Nc3 ∼ b 4 , (2.39c) h except for the case of a sphere Nc1, Nc depends on the aspect-ratio b/h. For a sphere self-avoidance is always important. But following [41] the dependence of Nc2 on the aspect-ratio squared is the most reasonable. E.g. for DNA the aspect-ratio is about 30 so that Nc2 ≈ 500 − 1000. This value is in the range of the number of segments used in the simulations. We do not know the prefactor in the scaling relations hence we cannot be sure whether self-avoidance must be taken into account. We will see in chapter 5, that up to N = 500 segments we could not detect any influence of self-avoidance on the static properties.
Page 1 and 2: Diploma Thesis Polymers in Confined
Page 3: TMTOWTDI—There’s More Than One
Page 7 and 8: Contents 1 Introduction 1 2 Polymer
Page 9 and 10: Chapter 1 Introduction Polymers are
Page 11 and 12: (a) λ-DNA (b) T2-DNA Figure 1.2: A
Page 13 and 14: Chapter 2 Polymer models This chapt
Page 15 and 16: 2.2. IDEAL PHANTOM CHAIN 7 configur
Page 17 and 18: 2.3. SEMI-FLEXIBLE POLYMERS 9 In th
Page 19 and 20: 2.3. SEMI-FLEXIBLE POLYMERS 11 to i
Page 21 and 22: 2.3. SEMI-FLEXIBLE POLYMERS 13 for
Page 23 and 24: 2.5. REAL CHAINS 15 no overhangs al
Page 25: 2.5. REAL CHAINS 17 Figure 2.5: Sna
Page 29 and 30: Chapter 3 Polymers in confined geom
Page 31 and 32: 3.2. SCALING RELATIONS 23 using eq.
Page 33 and 34: 3.2. SCALING RELATIONS 25 b a d R |
Page 35 and 36: 3.3. ANALYTICAL RESULTS 27 The mean
Page 37 and 38: 3.3. ANALYTICAL RESULTS 29 From thi
Page 39 and 40: 3.3. ANALYTICAL RESULTS 31 a consta
Page 41 and 42: 3.3. ANALYTICAL RESULTS 33 the proj
Page 43 and 44: 3.3. ANALYTICAL RESULTS 35 x 2 (s/
Page 45 and 46: Chapter 4 Simulation methods This c
Page 47 and 48: 4.3. SAMPLING THE CANONICAL ENSEMBL
Page 55 and 56: 4.4. SIMULATION OF UNCONFINED WORM-
Page 57 and 58: 4.4. SIMULATION OF UNCONFINED WORM-
Page 59 and 60: 4.5. SIMULATION OF CONFINED WORM-LI
Page 61 and 62: 4.6. SAMPLED QUANTITIES AND THEIR R
Page 63 and 64: 4.6. SAMPLED QUANTITIES AND THEIR R
Page 65 and 66: Chapter 5 Simulation results In thi
Page 67 and 68: 5.2. THE HARMONIC POTENTIAL 59 ˆt
Page 69 and 70: 5.2. THE HARMONIC POTENTIAL 61 5.2.
Page 71 and 72: 5.2. THE HARMONIC POTENTIAL 63 beha
Page 73 and 74: 5.2. THE HARMONIC POTENTIAL 65 R 2
Page 75 and 76: 5.2. THE HARMONIC POTENTIAL 67 R 2
Page 77 and 78:
5.2. THE HARMONIC POTENTIAL 69 R
Page 79 and 80:
5.2. THE HARMONIC POTENTIAL 71 p(R)
Page 81 and 82:
5.3. THE HARD WALLS 73 〈Ra〉 1 0
Page 83 and 84:
Chapter 6 Conclusion Emerging from
Page 85 and 86:
Appendix A Discrete worm-like chain
Page 87 and 88:
which, after taking all the derivat
Page 89 and 90:
Appendix B Calculation for the conf
Page 91 and 92:
B.2. END-TO-END DISTANCE CORRELATIO
Page 93 and 94:
B.3. PARALLEL END-TO-END DISTANCE C
Page 95 and 96:
Glossary L filament length lp persi
Page 97 and 98:
Bibliography [1] M. Abramowitz and
Page 99 and 100:
BIBLIOGRAPHY 91 [29] P. L’Ecuyer.
Page 101:
:wq
show all

Polymers in Confined Geometry.pdf

Create successful ePaper yourself

Delete template?

Save as template?