Polymers in Confined Geometry.pdf

5.2. THE HARMONIC POTENTIAL 67
R 2 /L 2
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
analytic
N = 50
N = 100
N = 500
N = 1000
1
1
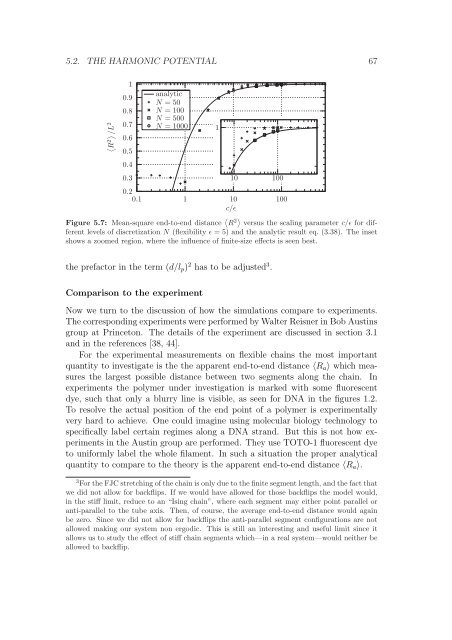
Figure 5.7: Mean-square end-to-end distance R 2 versus the scaling parameter c/ɛ for different
levels of discretization N (flexibility ɛ = 5) and the analytic result eq. (3.38). The inset
shows a zoomed region, where the influence of finite-size effects is seen best.
10
10
c/ɛ
the prefactor in the term (d/lp) 2 has to be adjusted 3 .
Comparison to the experiment
Now we turn to the discussion of how the simulations compare to experiments.
The corresponding experiments were performed by Walter Reisner in Bob Austins
group at Princeton. The details of the experiment are discussed in section 3.1
and in the references [38, 44].
For the experimental measurements on flexible chains the most important
quantity to investigate is the the apparent end-to-end distance 〈Ra〉 which measures
the largest possible distance between two segments along the chain. In
experiments the polymer under investigation is marked with some fluorescent
dye, such that only a blurry line is visible, as seen for DNA in the figures 1.2.
To resolve the actual position of the end point of a polymer is experimentally
very hard to achieve. One could imagine using molecular biology technology to
specifically label certain regimes along a DNA strand. But this is not how experiments
in the Austin group are performed. They use TOTO-1 fluorescent dye
to uniformly label the whole filament. In such a situation the proper analytical
quantity to compare to the theory is the apparent end-to-end distance 〈Ra〉.
3 For the FJC stretching of the chain is only due to the finite segment length, and the fact that
we did not allow for backflips. If we would have allowed for those backflips the model would,
in the stiff limit, reduce to an “Ising chain”, where each segment may either point parallel or
anti-parallel to the tube axis. Then, of course, the average end-to-end distance would again
be zero. Since we did not allow for backflips the anti-parallel segment configurations are not
allowed making our system non ergodic. This is still an interesting and useful limit since it
allows us to study the effect of stiff chain segments which—in a real system—would neither be
allowed to backflip.
100
100