Polymers in Confined Geometry.pdf

More documents

Recommendations

Info

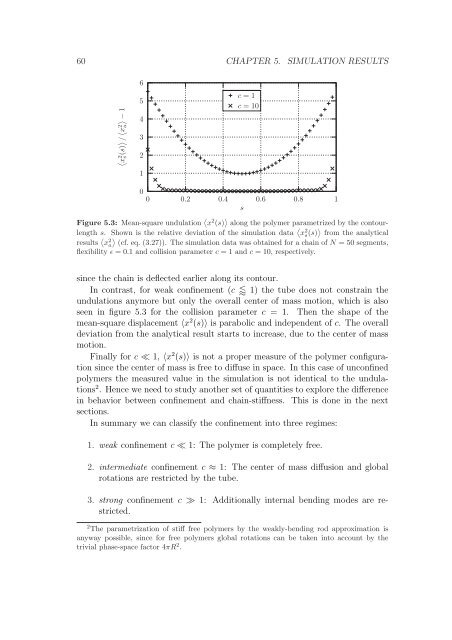
60 CHAPTER 5. SIMULATION RESULTS − 1 x 2 s (s) / x 2 a 6 5 4 3 2 1 0 0 0.2 0.4 c = 1 c = 10 Figure 5.3: Mean-square undulation x2 (s) along the polymer parametrized by the contourlength s. Shown is the relative deviation of the simulation data x2 s(s) from the analytical results x2 a (cf. eq. (3.27)). The simulation data was obtained for a chain of N = 50 segments, flexibility ɛ = 0.1 and collision parameter c = 1 and c = 10, respectively. since the chain is deflected earlier along its contour. In contrast, for weak confinement (c 1) the tube does not constrain the undulations anymore but only the overall center of mass motion, which is also seen in figure 5.3 for the collision parameter c = 1. Then the shape of the mean-square displacement 〈x 2 (s)〉 is parabolic and independent of c. The overall deviation from the analytical result starts to increase, due to the center of mass motion. Finally for c ≪ 1, 〈x 2 (s)〉 is not a proper measure of the polymer configuration since the center of mass is free to diffuse in space. In this case of unconfined polymers the measured value in the simulation is not identical to the undulations 2 . Hence we need to study another set of quantities to explore the difference in behavior between confinement and chain-stiffness. This is done in the next sections. In summary we can classify the confinement into three regimes: 1. weak confinement c ≪ 1: The polymer is completely free. 2. intermediate confinement c ≈ 1: The center of mass diffusion and global rotations are restricted by the tube. 3. strong confinement c ≫ 1: Additionally internal bending modes are restricted. 2 The parametrization of stiff free polymers by the weakly-bending rod approximation is anyway possible, since for free polymers global rotations can be taken into account by the trivial phase-space factor 4πR 2 . s 0.6 0.8 1
5.2. THE HARMONIC POTENTIAL 61 5.2.2 Tangent-tangent correlation Now we turn to investigate the tangent-tangent correlation function defined as φtt(s, s ′ ) = 〈t(s) · t(s ′ )〉 . (5.1) This allows us to extract some more information on the universal properties of our polymer system. The influence of the tube on the tangent-tangent correlation can be divided into three regimes, when the important length scale is again the Odijk deflection length 1/c: 1. For segments which are close enough along the chain the influence of the tube is negligible. Then, the tangent-tangent correlation decays exponentially as if for a free polymer until the segments get deflected by the ‘tube’. The free behavior is seen within the range 0 ≤ |s − s ′ | 1/c. 2. In the range of |s−s ′ | ≈ 1/c the first deflection of the segments takes place. This is seen in a intermediate flattening of the correlation function, or, for strong confinement, in a local minimum (see figs. 5.4). This feature indicates that the fluctuations of the tangent-tangent correlations around the mean 〈δt(s) · δt(s ′ )〉 = 〈t(s) · t(s ′ )〉 − 〈t〉 2 are anticorrelated in this range, due to the deflections. 3. For large distances along the chain |s − s ′ | ≫ 1/c the correlation function depends only on the ratio c/ɛ as expected from eq. (3.35) and becomes constant except for boundary effects. This is the universal behavior we expect for strong confinement. The three regimes can be identified by inspecting the plots in figure 5.4. The behavior of the tangent-tangent correlation for fixed stiffness ɛ = 0.1 is shown in figure 5.4(a) where the purely exponential behavior is seen for quasifree chains with c 1, i.e. on average less than one collision with the tube. Upon increasing the collision parameter, the correlation function develops a plateau. Figure 5.4(d) clearly displays all three regimes. The analytical results capture the exponential decay as well as the saturation of the correlation function but not the final decay at the ends. The deviation at the boundary is due to the free ends of the simulated chain. The overview plot figure 5.4(a) shows that boundary effects become less pronounced as the confinement becomes stronger. Then the behavior is dominated by the constant value of strong confinement, which depends only on the scaling parameter c/ɛ as expected from eq. (3.35). The behavior of the correlation function for intermediate confinement with c ≈ 3 is shown in 5.4(c). Here we observe a strong deviation from the analytical result, which is due to the boundary conditions. In this regime the specific choice of boundary conditions for analytical calculations is essential for the correct
Page 1 and 2:
Diploma Thesis Polymers in Confined
Page 3:
TMTOWTDI—There’s More Than One
Page 7 and 8:
Contents 1 Introduction 1 2 Polymer
Page 9 and 10:
Chapter 1 Introduction Polymers are
Page 11 and 12:
(a) λ-DNA (b) T2-DNA Figure 1.2: A
Page 13 and 14:
Chapter 2 Polymer models This chapt
Page 15 and 16:
2.2. IDEAL PHANTOM CHAIN 7 configur
Page 17 and 18: 2.3. SEMI-FLEXIBLE POLYMERS 9 In th
Page 19 and 20: 2.3. SEMI-FLEXIBLE POLYMERS 11 to i
Page 21 and 22: 2.3. SEMI-FLEXIBLE POLYMERS 13 for
Page 23 and 24: 2.5. REAL CHAINS 15 no overhangs al
Page 25 and 26: 2.5. REAL CHAINS 17 Figure 2.5: Sna
Page 27 and 28: 2.5. REAL CHAINS 19 ln R cases intr
Page 29 and 30: Chapter 3 Polymers in confined geom
Page 31 and 32: 3.2. SCALING RELATIONS 23 using eq.
Page 33 and 34: 3.2. SCALING RELATIONS 25 b a d R |
Page 35 and 36: 3.3. ANALYTICAL RESULTS 27 The mean
Page 37 and 38: 3.3. ANALYTICAL RESULTS 29 From thi
Page 39 and 40: 3.3. ANALYTICAL RESULTS 31 a consta
Page 41 and 42: 3.3. ANALYTICAL RESULTS 33 the proj
Page 43 and 44: 3.3. ANALYTICAL RESULTS 35 x 2 (s/
Page 45 and 46: Chapter 4 Simulation methods This c
Page 47 and 48: 4.3. SAMPLING THE CANONICAL ENSEMBL
Page 55 and 56: 4.4. SIMULATION OF UNCONFINED WORM-
Page 57 and 58: 4.4. SIMULATION OF UNCONFINED WORM-
Page 59 and 60: 4.5. SIMULATION OF CONFINED WORM-LI
Page 61 and 62: 4.6. SAMPLED QUANTITIES AND THEIR R
Page 63 and 64: 4.6. SAMPLED QUANTITIES AND THEIR R
Page 65 and 66: Chapter 5 Simulation results In thi
Page 67: 5.2. THE HARMONIC POTENTIAL 59 ˆt
Page 71 and 72: 5.2. THE HARMONIC POTENTIAL 63 beha
Page 73 and 74: 5.2. THE HARMONIC POTENTIAL 65 R 2
Page 75 and 76: 5.2. THE HARMONIC POTENTIAL 67 R 2
Page 77 and 78: 5.2. THE HARMONIC POTENTIAL 69 R
Page 79 and 80: 5.2. THE HARMONIC POTENTIAL 71 p(R)
Page 81 and 82: 5.3. THE HARD WALLS 73 〈Ra〉 1 0
Page 83 and 84: Chapter 6 Conclusion Emerging from
Page 85 and 86: Appendix A Discrete worm-like chain
Page 87 and 88: which, after taking all the derivat
Page 89 and 90: Appendix B Calculation for the conf
Page 91 and 92: B.2. END-TO-END DISTANCE CORRELATIO
Page 93 and 94: B.3. PARALLEL END-TO-END DISTANCE C
Page 95 and 96: Glossary L filament length lp persi
Page 97 and 98: Bibliography [1] M. Abramowitz and
Page 99 and 100: BIBLIOGRAPHY 91 [29] P. L’Ecuyer.
Page 101: :wq
show all

Polymers in Confined Geometry.pdf

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?