Low_resolution_Thesis_CDD_221009_public - Visual Optics and ...

CORRELATION BETWEEN RADIUS AND ASPHERICITY
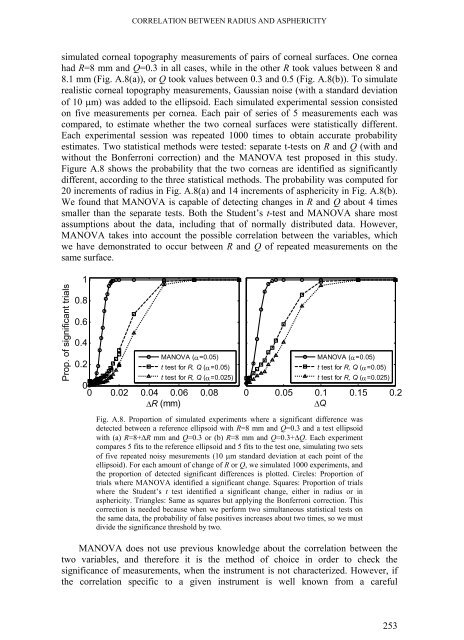
simulated corneal topography measurements of pairs of corneal surfaces. One cornea
had R=8 mm and Q=0.3 in all cases, while in the other R took values between 8 and
8.1 mm (Fig. A.8(a)), or Q took values between 0.3 and 0.5 (Fig. A.8(b)). To simulate
realistic corneal topography measurements, Gaussian noise (with a standard deviation
of 10 m) was added to the ellipsoid. Each simulated experimental session consisted
on five measurements per cornea. Each pair of series of 5 measurements each was
compared, to estimate whether the two corneal surfaces were statistically different.
Each experimental session was repeated 1000 times to obtain accurate probability
estimates. Two statistical methods were tested: separate t-tests on R and Q (with and
without the Bonferroni correction) and the MANOVA test proposed in this study.
Figure A.8 shows the probability that the two corneas are identified as significantly
different, according to the three statistical methods. The probability was computed for
20 increments of radius in Fig. A.8(a) and 14 increments of asphericity in Fig. A.8(b).
We found that MANOVA is capable of detecting changes in R and Q about 4 times
smaller than the separate tests. Both the Student’s t-test and MANOVA share most
assumptions about the data, including that of normally distributed data. However,
MANOVA takes into account the possible correlation between the variables, which
we have demonstrated to occur between R and Q of repeated measurements on the
same surface.
Prop. of significant trials
1
0.8
0.6
0.4
0.2
MANOVA (=0.05)
t test for R, Q (=0.05)
t test for R, Q (=0.025)
0
0 0.02 0.04 0.06 0.08
R (mm)
MANOVA (=0.05)
t test for R, Q (=0.05)
t test for R, Q (=0.025)
0 0.05 0.1 0.15 0.2
Q
Fig. A.8. Proportion of simulated experiments where a significant difference was
detected between a reference ellipsoid with R=8 mm and Q=0.3 and a test ellipsoid
with (a) R=8+R mm and Q=0.3 or (b) R=8 mm and Q=0.3+Q. Each experiment
compares 5 fits to the reference ellipsoid and 5 fits to the test one, simulating two sets
of five repeated noisy mesurements (10 m standard deviation at each point of the
ellipsoid). For each amount of change of R or Q, we simulated 1000 experiments, and
the proportion of detected significant differences is plotted. Circles: Proportion of
trials where MANOVA identified a significant change. Squares: Proportion of trials
where the Student’s t test identified a significant change, either in radius or in
asphericity. Triangles: Same as squares but applying the Bonferroni correction. This
correction is needed because when we perform two simultaneous statistical tests on
the same data, the probability of false positives increases about two times, so we must
divide the significance threshold by two.
MANOVA does not use previous knowledge about the correlation between the
two variables, and therefore it is the method of choice in order to check the
significance of measurements, when the instrument is not characterized. However, if
the correlation specific to a given instrument is well known from a careful
253