Wave Propagation in Linear Media | re-examined

P
2
1.5
1
0.5
0
0
2
X
4
0
4 One-dimensional quantum tunnelling
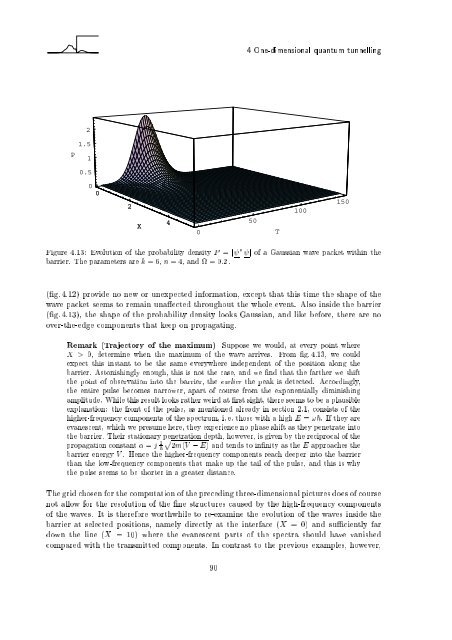
Figure 4.13: Evolution of the probability density P = j j of a Gaussian wave packet within the
barrier. The parameters are k =6,n=4,and =0:2.
( g. 4.12) provide no new or unexpected information, except that this time the shape of the
wave packet seems to remain una ected throughout the whole event. Also inside the barrier
( g. 4.13), the shape of the probability density looks Gaussian, and like before, there are no
over-the-edge components that keep on propagating.
Remark (Trajectory of the maximum) Suppose we would, at every point where
X > 0, determine when the maximum of the wave arrives. From g. 4.13, we could
expect this instant to be the same everywhere independent of the position along the
barrier. Astonishingly enough, this is not the case, and we nd that the farther we shift
the point of observation into the barrier, the earlier the peak is detected. Accordingly,
the entire pulse becomes narrower, apart of course from the exponentially diminishing
amplitude. While this result looks rather weird at rst sight, there seems to be a plausible
explanation: the front ofthe pulse, as mentioned already in section 2.1, consists of the
higher-frequency components of the spectrum, i. e. those with a high E = !~. If they are
evanescent, which we presume here, they experience no phase shift as they penetrate into
the barrier. Their stationary penetration depth, however, is given by the reciprocal of the
propagation constant = j 1p
~ 2m(V , E) and tends to in nity as the E approaches the
barrier energy V . Hence the higher-frequency components reach deeper into the barrier
than the low-frequency components that make up the tail of the pulse, and this is why
the pulse seems to be shorter in a greater distance.
The grid chosen for the computation of the preceding three-dimensional pictures does of course
not allow for the resolution of the ne structures caused by the high-frequency components
of the waves. It is therefore worthwhile to re-examine the evolution of the waves inside the
barrier at selected positions, namely directly at the interface (X = 0) and su ciently far
down the line (X = 10) where the evanescent parts of the spectra should have vanished
compared with the transmitted components. In contrast to the previous examples, however,
90
50
T
100
150