Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
17.5<br />
15<br />
12.5<br />
10<br />
7.5<br />
5<br />
2.5<br />
τ<br />
0.5 1 1.5 2 2.5 3 Ω<br />
35<br />
30<br />
25<br />
20<br />
15<br />
10<br />
5<br />
τ<br />
4 One-dimensional quantum tunnell<strong>in</strong>g<br />
0.5 1 1.5 2 2.5 3 Ω<br />
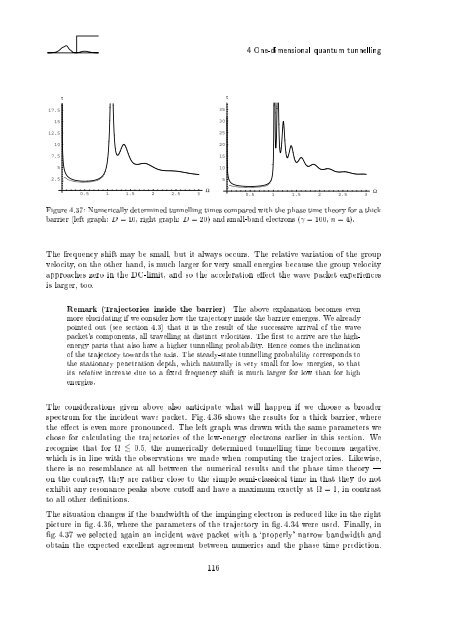
Figu<strong>re</strong> 4.37: Numerically determ<strong>in</strong>ed tunnell<strong>in</strong>g times compa<strong>re</strong>d with the phase time theory for a thick<br />
barrier (left graph: D = 10, right graph: D = 20) and small-band electrons ( = 100, n = 4).<br />
The f<strong>re</strong>quency shift may be small, but it always occurs. The <strong>re</strong>lative variation of the group<br />
velocity, on the other hand, is much larger for very small energies because the group velocity<br />
approaches zero <strong>in</strong> the DC-limit, and so the acceleration e ect the wave packet experiences<br />
is larger, too.<br />
Remark (Trajectories <strong>in</strong>side the barrier) The above explanation becomes even<br />
mo<strong>re</strong> elucidat<strong>in</strong>g if we consider how the trajectory <strong>in</strong>side the barrier emerges. We al<strong>re</strong>ady<br />
po<strong>in</strong>ted out (see section 4.3) that it is the <strong>re</strong>sult of the successive arrival of the wave<br />
packet's components, all travell<strong>in</strong>g at dist<strong>in</strong>ct velocities. The rst to arrive a<strong>re</strong> the highenergy<br />
parts that also have a higher tunnell<strong>in</strong>g probability. Hence comes the <strong>in</strong>cl<strong>in</strong>ation<br />
of the trajectory towards the axis. The steady-state tunnell<strong>in</strong>g probability cor<strong>re</strong>sponds to<br />
the stationary penetration depth, which naturally is very small for low energies, so that<br />
its <strong>re</strong>lative <strong>in</strong>c<strong>re</strong>ase due to a xed f<strong>re</strong>quency shift is much larger for low than for high<br />
energies.<br />
The considerations given above also anticipate what will happen if we choose a broader<br />
spectrum for the <strong>in</strong>cident wavepacket. Fig. 4.36 shows the <strong>re</strong>sults for a thick barrier, whe<strong>re</strong><br />
the e ect is even mo<strong>re</strong> pronounced. The left graph was drawn with the same parameters we<br />
chose for calculat<strong>in</strong>g the trajectories of the low-energy electrons earlier <strong>in</strong> this section. We<br />
<strong>re</strong>cognise that for . 0:5, the numerically determ<strong>in</strong>ed tunnell<strong>in</strong>g time becomes negative,<br />
which is <strong>in</strong> l<strong>in</strong>e with the observations we made when comput<strong>in</strong>g the trajectories. Likewise,<br />
the<strong>re</strong> is no <strong>re</strong>semblance at all between the numerical <strong>re</strong>sults and the phase time theory |<br />
on the contrary, they a<strong>re</strong> rather close to the simple semi-classical time <strong>in</strong> that they do not<br />
exhibit any <strong>re</strong>sonance peaks above cuto and have a maximum exactly at = 1, <strong>in</strong> contrast<br />
to all other de nitions.<br />
The situation changes if the bandwidth of the imp<strong>in</strong>g<strong>in</strong>g electron is <strong>re</strong>duced like <strong>in</strong> the right<br />
pictu<strong>re</strong> <strong>in</strong> g. 4.36, whe<strong>re</strong> the parameters of the trajectory <strong>in</strong> g. 4.34 we<strong>re</strong> used. F<strong>in</strong>ally, <strong>in</strong><br />
g. 4.37 we selected aga<strong>in</strong> an <strong>in</strong>cident wavepacket with a `properly' narrow bandwidth and<br />
obta<strong>in</strong> the expected excellent ag<strong>re</strong>ement between numerics and the phase time p<strong>re</strong>diction.<br />
116