Wave Propagation in Linear Media | re-examined

4.2 Initial wave forms
-60 -50 -40 -30 -20 -10
3
2
1
-1
Ψ0
X
0.12
0.1
0.08
0.06
0.04
0.02
A
-2 -1 1 2 ξ
-2 -1 1 2 ξ
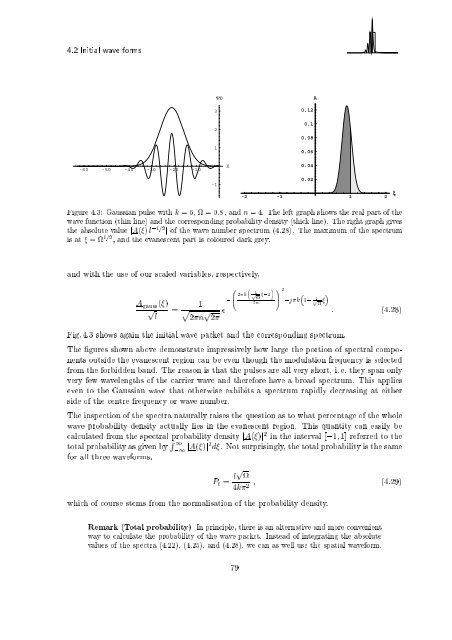
Figure 4.3: Gaussian pulse with k =6, =0:8 , and n =4. The left graph shows the real part of the
wave function (thin line) and the corresponding probability density (thick line). The right graph gives
the absolute value jA( ) l ,1=2 j of the wave number spectrum (4.28). The maximum of the spectrum
is at = 1=2 , and the evanescent part is coloured dark grey.
and with the use of our scaled variables, respectively,
A gauss ( )
p l
=
1
p 2 n p 2 e
,
0
@ 2 k p 1
,1
2n
1
A 2
,j k 1, 1
p
Fig. 4.3 shows again the initial wave packet and the corresponding spectrum.
: (4.28)
The gures shown above demonstrate impressively how large the portion of spectral components
outside the evanescent region can be even though the modulation frequency is selected
from the forbidden band. The reason is that the pulses are all very short, i. e. they span only
very few wavelengths of the carrier wave and therefore have a broad spectrum. This applies
even to the Gaussian wave that otherwise exhibits a spectrum rapidly decreasing at either
side of the centre frequency or wave number.
The inspection of the spectra naturally raises the question as to what percentage of the whole
wave probability density actually lies in the evanescent region. This quantity can easily be
calculated from the spectral probability density jA( )j 2 in the interval [,1; 1] referred to the
total probability as given by R 1
,1 jA( )j2 d . Not surprisingly, the total probability is the same
for all three waveforms,
Pt = lp
4k
2 ; (4.29)
which of course stems from the normalisation of the probability density.
Remark (Total probability) In principle, there is an alternative and more convenient
way to calculate the probability of the wave packet. Instead of integrating the absolute
values of the spectra (4.22), (4.25), and (4.28), we can as well use the spatial waveform.
79