- Page 1 and 2:
DISSERTATION Wave Propagation in Li
- Page 3:
Kurzfassung Seit der Entdeckung des
- Page 7 and 8:
Nullum est iam dictum, quod non sit
- Page 9 and 10:
Preface Our popular writers and rep
- Page 11 and 12:
the quest for superluminality and t
- Page 13 and 14:
Contents Part I Wave propagation ph
- Page 15 and 16:
7.3.4 PartitionPoints . . . . . . .
- Page 17 and 18:
Part I Wave propagation phenomena S
- Page 19 and 20:
1.1 Phase and group velocity 1.1 Ph
- Page 21 and 22:
1.1 Phase and group velocity ! !c v
- Page 23 and 24:
1.2 A few notes on dispersion He co
- Page 25 and 26:
1.2 A few notes on dispersion v/c 6
- Page 27 and 28:
1.3 Signal velocity dipoles with a
- Page 29 and 30:
1.3 Signal velocity The arbitrarine
- Page 31 and 32:
1.4 Energy velocity For electromagn
- Page 33 and 34:
1.5 Other velocity de nitions For n
- Page 35 and 36:
1.5 Other velocity de nitions evide
- Page 37 and 38:
2.1 Superluminal wave propagation 2
- Page 39 and 40:
2.1 Superluminal wave propagation a
- Page 41 and 42:
2.1 Superluminal wave propagation t
- Page 43 and 44:
2.2 Quantum mechanical tunnelling e
- Page 45 and 46:
2.2 Quantum mechanical tunnelling R
- Page 47 and 48:
Chapter 3 Wave propagation in elect
- Page 49 and 50:
3.1 Model of a transmission line th
- Page 51 and 52:
3.2 Excursion: a delay line section
- Page 53 and 54:
3.3 Re ection due to termination mi
- Page 55 and 56:
3.4 A simple thought experiment I0
- Page 57 and 58:
3.5 A dispersive system: the lossle
- Page 59 and 60:
3.5 A dispersive system: the lossle
- Page 61 and 62:
3.5 A dispersive system: the lossle
- Page 63 and 64:
3.6 Inhomogeneous transmission line
- Page 65 and 66:
3.7 Turn-on e ects in a lossless pl
- Page 67 and 68:
3.7 Turn-on e ects in a lossless pl
- Page 69 and 70:
3.7 Turn-on e ects in a lossless pl
- Page 71 and 72:
3.7 Turn-on e ects in a lossless pl
- Page 73 and 74:
3.7 Turn-on e ects in a lossless pl
- Page 75 and 76:
3.7 Turn-on e ects in a lossless pl
- Page 77 and 78:
3.8 Turn-on e ects in a wave guide
- Page 79 and 80:
3.8 Turn-on e ects in a wave guide
- Page 81 and 82:
3.9 A Gaussian pulse in plasma Like
- Page 83 and 84:
3.9 A Gaussian pulse in plasma 250
- Page 85 and 86:
3.9 A Gaussian pulse in plasma 250
- Page 87 and 88:
3.9 A Gaussian pulse in plasma Note
- Page 89 and 90:
4.1 The potential step 4.1 The pote
- Page 91 and 92:
4.1 The potential step Inside the b
- Page 93 and 94:
4.2 Initial wave forms -60 -50 -40
- Page 95 and 96:
4.2 Initial wave forms -60 -50 -40
- Page 97 and 98:
4.3 Examples of scattering processe
- Page 99 and 100: 4.3 Examples of scattering processe
- Page 101 and 102: 4.3 Examples of scattering processe
- Page 103 and 104: 4.3 Examples of scattering processe
- Page 105 and 106: 4.3 Examples of scattering processe
- Page 107 and 108: 4.3 Examples of scattering processe
- Page 109 and 110: 4.4 The square barrier they have va
- Page 111 and 112: 4.4 The square barrier 1 0.8 0.6 0.
- Page 113 and 114: 4.5 Tunnelling time de nitions for
- Page 115 and 116: 4.5 Tunnelling time de nitions for
- Page 117 and 118: 4.6 Examples of tunnelling events P
- Page 119 and 120: 4.6 Examples of tunnelling events 2
- Page 121 and 122: 4.6 Examples of tunnelling events -
- Page 123 and 124: 4.6 Examples of tunnelling events t
- Page 125 and 126: 4.6 Examples of tunnelling events P
- Page 127 and 128: 4.6 Examples of tunnelling events 8
- Page 129 and 130: 4.6 Examples of tunnelling events 8
- Page 131 and 132: 4.6 Examples of tunnelling events 7
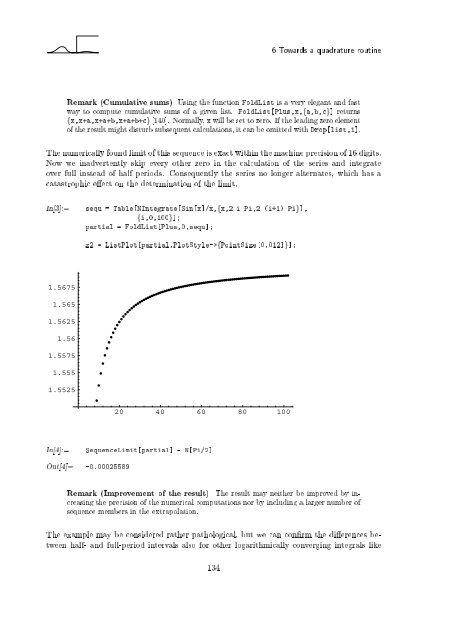
- Page 133 and 134: 4.6 Examples of tunnelling events T
- Page 135 and 136: Interlude Wave functions in graphic
- Page 137 and 138: Wave functions in graphical represe
- Page 139 and 140: Part II Numerical aspects of wave e
- Page 141 and 142: 5.1 Univariate numerical quadrature
- Page 143 and 144: 5.1 Univariate numerical quadrature
- Page 145 and 146: 5.2 Convergence acceleration one, t
- Page 147 and 148: 5.2 Convergence acceleration (1) ,1
- Page 149: 6.1 Partitioning the integration in
- Page 153 and 154: 6.1 Partitioning the integration in
- Page 155 and 156: 6.2 Choosing the rst partition poin
- Page 157 and 158: 6.3 How to compute the rst integral
- Page 159 and 160: 6.3 How to compute the rst integral
- Page 161 and 162: 6.4 Asymptotic partition consuming
- Page 163 and 164: 6.4 Asymptotic partition of the int
- Page 165 and 166: 6.5 Considerations for a Mathematic
- Page 167 and 168: 6.5 Considerations for a Mathematic
- Page 169 and 170: 6.5 Considerations for a Mathematic
- Page 171 and 172: 6.6 Controlling the accuracy of the
- Page 173 and 174: 6.6 Controlling the accuracy of the
- Page 175 and 176: 6.6 Controlling the accuracy of the
- Page 177 and 178: Chapter 7 Mathematica implementatio
- Page 179 and 180: 7.1 User interface of the function
- Page 181 and 182: 7.3 Implementation of OscInt and re
- Page 183 and 184: 7.3 Implementation of OscInt and re
- Page 185 and 186: 7.3 Implementation of OscInt and re
- Page 187 and 188: 7.3 Implementation of OscInt and re
- Page 189 and 190: 7.4 Auxiliary functions While[itera
- Page 191 and 192: 7.4 Auxiliary functions Linear appr
- Page 193 and 194: 7.4 Auxiliary functions For the sak
- Page 195 and 196: 7.4 Auxiliary functions Out[8]= 3 f
- Page 197 and 198: 7.5 Test of the quadrature routine
- Page 199 and 200: 7.5 Test of the quadrature routine
- Page 201 and 202:
7.5 Test of the quadrature routine
- Page 203 and 204:
7.5 Test of the quadrature routine
- Page 205 and 206:
7.5 Test of the quadrature routine
- Page 207 and 208:
8.1 Preparation of the wave integra
- Page 209 and 210:
8.1 Preparation of the wave integra
- Page 211 and 212:
8.1 Preparation of the wave integra
- Page 213 and 214:
8.2 Outline of the program structur
- Page 215 and 216:
8.2 Outline of the program structur
- Page 217 and 218:
8.3 Implementation of the quadratur
- Page 219 and 220:
8.3 Implementation of the quadratur
- Page 221 and 222:
8.4 Test of the package 8.4 Test of
- Page 223 and 224:
8.4 Test of the package -200 -150 -
- Page 225 and 226:
8.4 Test of the package 0.4 0.2 -0.
- Page 227 and 228:
8.4 Test of the package 8.4.2 Forma
- Page 229 and 230:
8.4 Test of the package Out[24]= 0
- Page 231 and 232:
A.1 Numerical quadrature Asymptotic
- Page 233 and 234:
A.1 Numerical quadrature WynnDegree
- Page 235 and 236:
A.1 Numerical quadrature Which[ft =
- Page 237 and 238:
A.2 Solutions for the step potentia
- Page 239 and 240:
A.2 Solutions for the step potentia
- Page 241 and 242:
A.2 Solutions for the step potentia
- Page 243 and 244:
A.2 Solutions for the step potentia
- Page 245 and 246:
A.3 Solutions for the square barrie
- Page 247 and 248:
A.3 Solutions for the square barrie
- Page 249 and 250:
A.4 Electromagnetic waves function
- Page 251 and 252:
A.5 Utilities for displaying points
- Page 253 and 254:
Bibliography Bibliography [1] James
- Page 255 and 256:
Bibliography [29] Kurt Edmund Oughs
- Page 257 and 258:
Bibliography [59] Ch. Spielmann, R.
- Page 259 and 260:
Bibliography [91] C. R. Leavens and
- Page 261 and 262:
Bibliography [123] T. O. Espelid an
- Page 263 and 264:
Index Index absorption, 7, 9 accura
- Page 265 and 266:
Index saddle point integration, 11,
- Page 267:
Curriculum vitae Dipl.-Ing. Thilo S