Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
4.6 Examples of tunnell<strong>in</strong>g events<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
τ<br />
0.5 1 1.5 2 2.5 3 Ω<br />
8<br />
6<br />
4<br />
τ<br />
0.5 1 1.5 2 2.5 3 Ω<br />
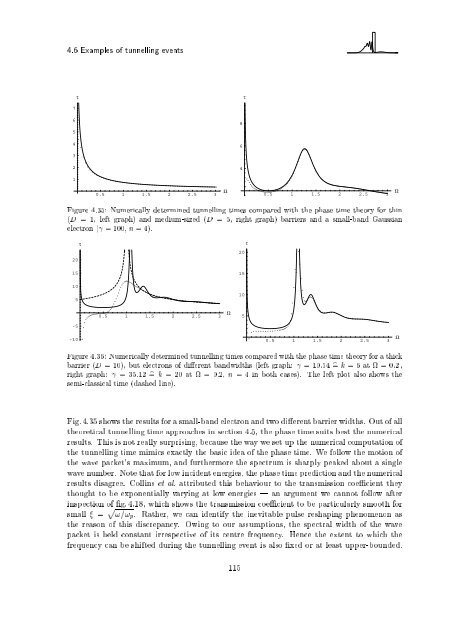
Figu<strong>re</strong> 4.35: Numerically determ<strong>in</strong>ed tunnell<strong>in</strong>g times compa<strong>re</strong>d with the phase time theory for th<strong>in</strong><br />
(D = 1, left graph) and medium-sized (D = 5, right graph) barriers and a small-band Gaussian<br />
electron ( = 100, n = 4).<br />
20<br />
15<br />
10<br />
5<br />
-5<br />
-10<br />
τ<br />
0.5 1 1.5 2 2.5 3 Ω<br />
20<br />
15<br />
10<br />
5<br />
τ<br />
0.5 1 1.5 2 2.5 3 Ω<br />
Figu<strong>re</strong> 4.36: Numerically determ<strong>in</strong>ed tunnell<strong>in</strong>g times compa<strong>re</strong>d with the phase time theory for a thick<br />
barrier (D = 10), but electrons of di e<strong>re</strong>nt bandwidths (left graph: =10:54 b= k = 6 at = 0:2,<br />
right graph: = 35:12 b= k = 20 at = 0:2, n = 4 <strong>in</strong> both cases). The left plot also shows the<br />
semi-classical time (dashed l<strong>in</strong>e).<br />
Fig. 4.35 shows the <strong>re</strong>sults for a small-band electron and two di e<strong>re</strong>nt barrier widths. Out of all<br />
theo<strong>re</strong>tical tunnell<strong>in</strong>g time approaches <strong>in</strong> section 4.5, the phase time suits best the numerical<br />
<strong>re</strong>sults. This is not <strong>re</strong>ally surpris<strong>in</strong>g, because the way we set up the numerical computation of<br />
the tunnell<strong>in</strong>g time mimics exactly the basic idea of the phase time. We follow the motion of<br />
the wave packet's maximum, and furthermo<strong>re</strong> the spectrum is sharply peaked about a s<strong>in</strong>gle<br />
wave number. Note that for low <strong>in</strong>cident energies, the phase time p<strong>re</strong>diction and the numerical<br />
<strong>re</strong>sults disag<strong>re</strong>e. Coll<strong>in</strong>s et al. attributed this behaviour to the transmission coe cient they<br />
thought to be exponentially vary<strong>in</strong>g at low energies | an argument we cannot follow after<br />
<strong>in</strong>spection of g. 4.18, which shows the transmission coe cient to be particularly smooth for<br />
small = p !=!p. Rather, we can identify the <strong>in</strong>evitable pulse <strong>re</strong>shap<strong>in</strong>g phenomenon as<br />
the <strong>re</strong>ason of this disc<strong>re</strong>pancy. Ow<strong>in</strong>g to our assumptions, the spectral width of the wave<br />
packet is held constant ir<strong>re</strong>spective of its cent<strong>re</strong> f<strong>re</strong>quency. Hence the extent to which the<br />
f<strong>re</strong>quency can be shifted dur<strong>in</strong>g the tunnell<strong>in</strong>g event is also xed or at least upper-bounded.<br />
115