Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Wave Propagation in Linear Media | re-examined
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
0.5<br />
-0.5<br />
I/I0<br />
-1<br />
3<strong>Wave</strong> propagation <strong>in</strong> electromagnetic transmission l<strong>in</strong>es<br />
100 125 150 175 200 225 250 275<br />
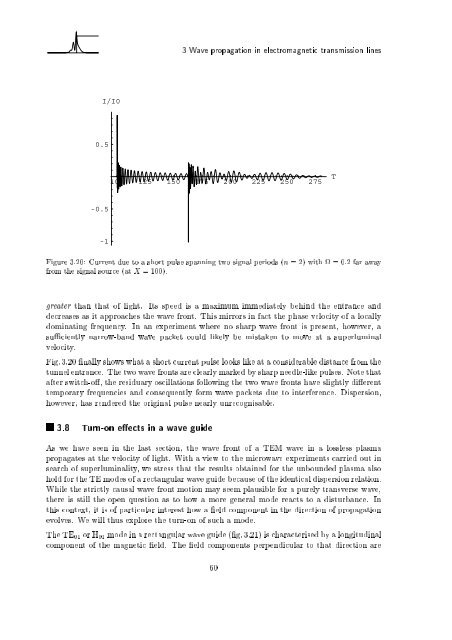
Figu<strong>re</strong> 3.20: Cur<strong>re</strong>nt due to a short pulse spann<strong>in</strong>g two signal periods (n = 2) with = 0:2 far away<br />
from the signal source (at X = 100).<br />
g<strong>re</strong>ater than that of light. Its speed is a maximum immediately beh<strong>in</strong>d the entrance and<br />
dec<strong>re</strong>ases as it approaches the wave front. This mirrors <strong>in</strong> fact the phase velocity of a locally<br />
dom<strong>in</strong>at<strong>in</strong>g f<strong>re</strong>quency. In an experiment whe<strong>re</strong> no sharp wave front is p<strong>re</strong>sent, however, a<br />
su ciently narrow-band wave packet could likely be mistaken to move at a superlum<strong>in</strong>al<br />
velocity.<br />
Fig. 3.20 nally shows what a short cur<strong>re</strong>nt pulse looks like at a considerable distance from the<br />
tunnel entrance. The twowave fronts a<strong>re</strong> clearly marked by sharp needle-like pulses. Note that<br />
after switch-o , the <strong>re</strong>siduary oscillations follow<strong>in</strong>g the two wave fronts have slightly di e<strong>re</strong>nt<br />
temporary f<strong>re</strong>quencies and consequently form wave packets due to <strong>in</strong>terfe<strong>re</strong>nce. Dispersion,<br />
however, has <strong>re</strong>nde<strong>re</strong>d the orig<strong>in</strong>al pulse nearly un<strong>re</strong>cognisable.<br />
3.8 Turn-on e ects <strong>in</strong> a wave guide<br />
As we have seen <strong>in</strong> the last section, the wave front of a TEM wave <strong>in</strong> a lossless plasma<br />
propagates at the velocity of light. With a view to the microwave experiments carried out <strong>in</strong><br />
search of superlum<strong>in</strong>ality, we st<strong>re</strong>ss that the <strong>re</strong>sults obta<strong>in</strong>ed for the unbounded plasma also<br />
hold for the TE modes of a <strong>re</strong>ctangular wave guide because of the identical dispersion <strong>re</strong>lation.<br />
While the strictly causal wave front motion may seem plausible for a pu<strong>re</strong>ly transverse wave,<br />
the<strong>re</strong> is still the open question as to how a mo<strong>re</strong> general mode <strong>re</strong>acts to a disturbance. In<br />
this context, it is of particular <strong>in</strong>te<strong>re</strong>st how a eld component <strong>in</strong> the di<strong>re</strong>ction of propagation<br />
evolves. We will thus explo<strong>re</strong> the turn-on of such a mode.<br />
The TE01 or H01 mode <strong>in</strong> a <strong>re</strong>ctangular wave guide ( g. 3.21) is characterised by a longitud<strong>in</strong>al<br />
component of the magnetic eld. The eld components perpendicular to that di<strong>re</strong>ction a<strong>re</strong><br />
60<br />
T