Wave Propagation in Linear Media | re-examined

7.5
5
2.5
-2.5
-5
-7.5
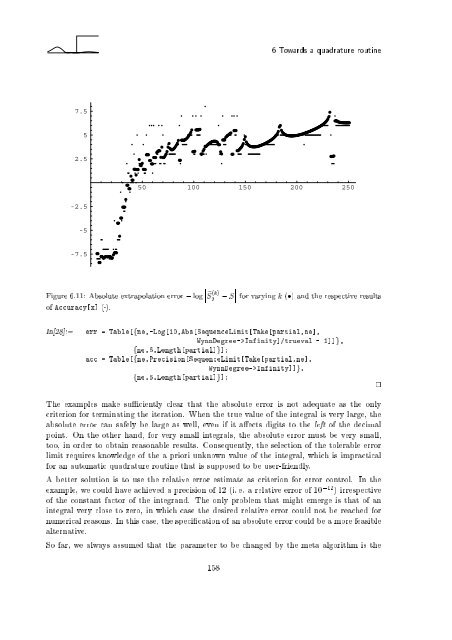
Figure 6.11: Absolute extrapolation error , log e S (k)
0
of Accuracy[x] ( ).
6Towards a quadrature routine
50 100 150 200 250
, S for varying k ( ) and the respective results
In[28]:= err = Table[fne,-Log[10,Abs[SequenceLimit[Take[partial,ne],
WynnDegree->Infinity]/trueval - 1]]g,
fne,6,Length[partial]g];
acc = Table[fne,Precision[SequenceLimit[Take[partial,ne],
WynnDegree->Infinity]]g,
fne,6,Length[partial]g];
The examples make su ciently clear that the absolute error is not adequate as the only
criterion for terminating the iteration. When the true value of the integral is very large, the
absolute error can safely be large as well, even if it a ects digits to the left of the decimal
point. On the other hand, for very small integrals, the absolute error must be very small,
too, in order to obtain reasonable results. Consequently, the selection of the tolerable error
limit requires knowledge of the a priori unknown value of the integral, which is impractical
for an automatic quadrature routine that is supposed to be user-friendly.
A better solution is to use the relative error estimate as criterion for error control. In the
example, we could have achieved a precision of 12 (i. e. a relative error of 10 ,12 ) irrespective
of the constant factor of the integrand. The only problem that might emerge is that of an
integral very close to zero, in which case the desired relative error could not be reached for
numerical reasons. In this case, the speci cation of an absolute error could be a more feasible
alternative.
So far, we always assumed that the parameter to be changed by the meta algorithm is the
158