Pr´ıklady k predmetu Matematika 4
Pr´ıklady k predmetu Matematika 4
Pr´ıklady k predmetu Matematika 4
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Příklady k předmětu <strong>Matematika</strong> 4<br />
Verze ze dne 12. ledna 2012<br />
Jan Chleboun<br />
Obsah<br />
Úvod ................................................................... 2<br />
1 Vlastní čísla a vlastní vektory matic ..................................... 3<br />
2 Aplikace Geršgorinovy věty: vlastní čísla matic . . . ....................... 13<br />
3 Aplikace Geršgorinovy věty: odhad čísla podmíněnosti . . ................. 21<br />
4 Normy vektorů a matic . . ............................................... 23<br />
5 Gaussova eliminace . . . .................................................. 27<br />
6 Iterační metody. . . ...................................................... 27<br />
7 Lineární zobrazení ...................................................... 32<br />
8 Okrajové úlohy v 1D: řešitelnost ................... . .................... 36<br />
9 Pozitivní definitnost operátorů . . ........................................ 39<br />
10 Pozitivní definitnost operátorů,<br />
Ritzova metoda . . . ...................................................... 48<br />
11 Pozitivní definitnost operátorů,<br />
metoda sítí . ............................................................ 58<br />
12 Metoda sítí v 1D: okrajové úlohy . . . ................ . .................... 62<br />
13 Metoda sítí v 1D: vlastní čísla okrajových úloh . ......................... 66<br />
14 Metoda sítí ve 2D: Liebmannova iterace ............... . ................. 69<br />
15 Metoda sítí ve 2D: Dirichletova úloha . . ................................. 70<br />
16 Metoda sítí ve 2D: vlnová rovnice . . ..................................... 75<br />
17 Metoda sítí ve 2D: rovnice vedení tepla . ................................. 80<br />
Literatura .................................................................. 85
Úvod<br />
Tato sbírka sestává především z příkladů, s nimiž se v minulých letech posluchači potýkali<br />
během zkoušek.<br />
Zkouškové příklady v právě aktuálním semestru nemusejí být jen triviálními obměnami<br />
zde uvedených problémů, ale při zvládnutí úloh z této sbírky mohou studenti a studentky<br />
jít ke zkoušce se sebedůvěrou a s velkou nadějí na získání lepšího hodnocení než D.<br />
Řada příkladů je poměrně podrobně vyřešena. Způsob, jakým je řešení podáno, však<br />
není učebnicově výkladový, místy je zkratkovitý nebo mírně nelogický. Proč tomu tak je,<br />
to vysvětluje poznámka v úvodu kapitoly 9. Řešení poskytuje dostatek detailů, nicméně<br />
se předpokládá, že čtenář se v látce orientuje a že užívá přinejmenším texty [3], [4] a [5].<br />
Velmi užitečná, ale dnes hůře dostupná, jsou skripta [2]. U příkladů, jež jsou jen malými<br />
obměnami podrobně vyřešené úlohy, jsou uvedeny alespoň závěrečné výsledky, případně<br />
i výsledky mezikroků.<br />
Studujícím doporučuji, aby nezůstali jen u mechanického naučení se postupů, jak<br />
příklady řešit, ale aby se snažili pochopit logické úvahy vedoucí k řešení. 1 Například úlohy<br />
v kapitole 1 se zdají být dosti různorodé, nicméně jejich řešení vždy vyplývá z nemnoha<br />
elementárních vlastností vlastních čísel a vlastních vektorů matice. Jednoduché využití<br />
těchto vlastností pak vede k následné algebraické úloze (hledání kořenů charakteristického<br />
polynomu, sestavení rovnic pro neznámé prvky matice aj.), jejíž vyřešení, jakož i dořešení<br />
výchozího problému se děje standardními postupy.<br />
Naučte se formulovat odpovědi a jejich zdůvodnění. Správná odpověd’ bez zdůvodnění<br />
je považována za neplatnou a v písemné práci nepřinese bodový zisk.<br />
Věnujte pozornost i zkouškám správnosti dílčích a hlavních výsledků, a to zejména<br />
v případech, kdy taková zkouška je velmi jednoduchá a časově nenáročná. Kolik cenných<br />
bodů už studující ztratili tím, že si neověřili, zda správně vyřešili soustavu lineárních<br />
rovnic nebo kvadratickou rovnici, zda panuje soulad mezi vypočeným vlastním číslem<br />
a vlastním vektorem a zda vypočtený výsledek je vůbec možný, například vyjde-li určitý<br />
integrál z kladné funkce záporně (to je chyba opravdu trestuhodná).<br />
Zkouškové příklady a jejich řešení pocházejí z materiálů, které se používají při opravování<br />
písemných prací. Záměrně jsem na několika místech ponechal návodné poznámky<br />
pro opravující pedagogy, co při opravování sledovat a na co být přísný. Můžete si z nich<br />
udělat lepší představu o důrazech při hodnocení správnosti řešení.<br />
Elektronické podklady pro sazbu jsem se snažil upravit tak, aby se například používala<br />
jednotná matematická symbolika a detailnost návodů byla jakž takž vyrovnaná. Výsledek<br />
jsem podrobil jen rychlé autokorektuře, očekávám tedy, že řada tiskových chyb mi unikla.<br />
Budu rád, když je naleznete a upozorníte mě na ně.<br />
1 K budování takového intelektuálního zázemí slouží i návštěva přenášky z MA 4, kde je, na rozdíl od<br />
cvičení, čas na výklad souvislostí.<br />
2
1 Vlastní čísla a vlastní vektory matic<br />
⎛<br />
−1 1<br />
⎞<br />
1<br />
Příklad 1.1: O matici M = ⎝ 1 −1 2 ⎠ je známo, že její vlastní čísla jsou λ 1 = −3,<br />
1 2 −1<br />
λ 2 = − √ 3 a λ 3 = √ 3. Určete největší a nejmenší vlastní číslo matice M −1 .<br />
Řešení: Vlastní čísla matice M −1 se rovnají převráceným hodnotám vlastních čísel matice<br />
M. Hledaná vlastní čísla tedy jsou λ −1<br />
3 = 1/ √ 3 = √ 3/3 a λ −1<br />
2 = −1/ √ 3 = − √ 3/3.<br />
Poznámka: Vyřešení předchozí úlohy snadno vyplývá z jedné z vlastností vlastních čísel.<br />
Jiné základní vlastnosti (více [4]) jsou předvedeny ⎛ například ⎞ v těchto úlohách:<br />
7 5 1<br />
Je λ = 1 + i vlastním číslem matice A = ⎝5 2 3 ⎠<br />
1 3 −1<br />
(Není, protože A je symetrická, a tudíž všechna její vlastní čísla jsou reálná.)<br />
⎛<br />
⎞<br />
7 5 1 6<br />
Je λ = 1 + i vlastním číslem matice A = ⎜0 2 3 1<br />
⎟<br />
⎝0 0 1 + i −2⎠ <br />
0 0 0 9<br />
(Ano, je, protože vlastní čísla trojúhelníkové matice jsou totožná s prvky na hlavní diagonále<br />
(zamyslete se nad tím, jak vypadá charakteristický polynom).)<br />
Příklad 1.2: ⎛Najděte aspoň ⎞ jednu takovou dvojici reálných čísel a a b, aby vlastní čísla<br />
3 a 1<br />
matice A = ⎝−1 4 2 ⎠ byla reálná, postup zdůvodněte.<br />
1 b −2<br />
Řešení: Vlastní čísla reálné symetrické matice jsou reálná. Stačí zvolit a = −1 a b = 2.<br />
Příklad ( 1.3: ) Najděte aspoň jednu čtveřici čísel a, b, c a d takovou, aby matice A =<br />
a + b a − c<br />
měla vlastní čísla λ<br />
b + 2c a + d<br />
1 = −1 a λ 2 = 1.<br />
Řešení: Jelikož horní trojúhelníková matice má vlastní čísla identická s prvky na hlavní<br />
diagonále, hledejme vhodnou horní trojúhelníkovou matice. Stačí se tedy zabývat soustavou<br />
a + b = −1, a − c = 0, b + 2c = 0, a + d = 1,<br />
jejíž řešení je a = 1, b = −2, c = 1, d = 0.<br />
Příklad 1.4: Najděte vlastní čísla a vlastní vektory matice<br />
⎛<br />
4<br />
⎞<br />
2 −1<br />
A = ⎝−1 4 1 ⎠ .<br />
−1 4 4<br />
(Nápověda: Vlastní čísla této matice jsou malá přirozená čísla.)<br />
Řešení: Kořeny charakteristického polynomu<br />
(4 − λ) 3 + 3λ − 10 = λ 3 − 12λ 2 + 45λ − 54<br />
3
se hledají zkusmo dosazováním malých celých čísel 0, 1, −1, 2, −2, 3, −3, . . .. Snáze se<br />
vyčísluje výraz vlevo, tj. před roznásobením. Po nalezení prvního kořene (tj. 3) lze charakteristický<br />
polynom vydělit členem λ − 3 a určit kořeny podílu, tedy vyřešit kvadratickou<br />
rovnici. Nebo je možné dosazováním najít i další kořen (tj. 6), a pak charakteristický<br />
polynom podělit kvadratickým členem (λ − 3)(λ − 6) = λ 2 − 9λ + 18. Podílem je lineární<br />
polynom s kořenem λ = 3.<br />
(Poznámka: Dosazováním můžeme najít kořen polynomu, ale nemůžeme odhalit, že<br />
je násobný, v našem případě je to kořen λ = 3. Snížíme tedy stupeň charakteristického<br />
polynomu dělením a hledáme kořeny výsledného podílu. Jiný postup hledání násobných<br />
kořenů spočívá v nalezení kořenů derivace charakteristického polynomu. Platí totiž, že pokud<br />
nějaké číslo je násobným kořenem polynomu, je také kořenem jeho derivace. Například<br />
náš charakteristický polynom má derivaci 3 (1 − (4 − λ) 2 ), jejímž kořenem je opět λ = 3.<br />
Další možností je využít toho, že součet prvků na hlavní diagonále matice, tj. 4+4+4 = 12,<br />
je roven součtu vlastních čísel uvažovaných i s jejich násobnostmi. Po nalezení vlastních<br />
čísel 3 a 6 dostáváme vlastní číslo 12 − 3 − 6 = 3.)<br />
Vlastní čísla jsou 3, 3, 6, příslušné vlastní vektory (1, 0, 1) T a (0, 1/2, 1) T (a jejich nenulové<br />
násobky komplexním číslem).<br />
Příklad 1.5: Najděte vlastní čísla a vlastní vektory matice<br />
⎛ ⎞<br />
−2 −1 −3<br />
A = ⎝ 4 3 3 ⎠.<br />
1 1 2<br />
(Nápověda: Vlastní čísla této matice jsou malá celá čísla.)<br />
Řešení: Charakteristický polynom<br />
(−2 − λ)(3 − λ)(2 − λ) − 3 − 12 + 3(3 − λ) + 4(2 − λ) + 3(2 + λ)<br />
= (λ 2 − 4)(3 − λ) + 8 − 4λ = −λ 3 + 3λ 2 − 4.<br />
Vlastní čísla jsou 2, 2, −1, příslušné vlastní vektory (−1, 1, 1) T a (−1, 1, 0) T (a jejich nenulové(!!)<br />
násobky komplexním číslem).<br />
Někteří studenti obcházejí výpočet determinantu jinou dosazovací metodou, totiž tím,<br />
že pro různé hodnoty λ zkoumají lineární (ne)závislost řádků matice A − λI. To je OK,<br />
v této úloze to dokonce není ani moc těžkopádné. Dvojnásobnost vlastního čísla 2 se tím<br />
však neodhalí.<br />
( ) 5 −8<br />
Příklad 1.6: Je dána matice A = . Nalezněte vlastní čísla a vlastní vektory<br />
−2 5<br />
matic B a B −1 , kde B = A 3 , tj. B = AAA.<br />
Řešení: Předpokládejme, že λ je vlastní číslo matice A a u je příslušný vlastní vektor.<br />
Z Au = λu plyne Bu = AAAu = AAλu = Aλ 2 u = λ 3 u a B −1 u = λ −3 u.<br />
Vlastní čísla matice A jsou 1 a 9, tedy vlastní čísla matice B jsou 1 a 9 3 = 3 6 = 729<br />
a vlastní čísla matice B −1 jsou 1 a 9 −3 = 3 −6 = 1/729.<br />
Matice A, B a B −1 mají tytéž vlastní vektory v 1 =<br />
(<br />
2<br />
1)<br />
p a v 2 =<br />
( )<br />
2<br />
q, kde p, q ∈<br />
−1<br />
C \ {0}.<br />
Jestliže student nejprve vypočte matici B, nebo dokonce B −1 , a pak počítá jejich<br />
vlastní čísla a vektory, dejte plný počet bodů, pokud jsou výsledky správné; k případným<br />
4
numerickým chybám však nebud’te shovívaví — at’ nese riziko toho, když dělá věci zbytečně<br />
složitě.<br />
Příklad 1.7: Jsou dány matice<br />
A =<br />
( ) −1 1<br />
3 1<br />
a B =<br />
( ) 4 a<br />
.<br />
1 b<br />
Nalezněte hodnoty a, b ∈ R takové, aby matice B měla stejná vlastní čísla jako matice A.<br />
Řešení: Charakteristický polynom matice A jest (−1 − λ)(1 − λ) − 3 s kořeny 2 a −2.<br />
Charakteristická rovnice matice B jest (4 − λ)(b − λ) − a = 0 a pro λ = 2, λ = −2<br />
z ní získáme soustavu<br />
její řešení: a = −12, b = −4.<br />
2b − a = 4<br />
6b − a = −12,<br />
Příklad 1.8: Je dána matice A a její vlastní vektor u příslušný jistému neznámému<br />
vlastnímu číslu:<br />
⎛<br />
−2 2<br />
⎞<br />
−7<br />
⎛ ⎞<br />
23<br />
A = ⎝ 7 3 7 ⎠ , u = ⎝ 0 ⎠ p, p ∈ C \ {0}.<br />
−2 −2 3<br />
−23<br />
Najděte všechna vlastní čísla matice A a všechny zbývající vlastní vektory matice A.<br />
⎛ ⎞ ⎛ ⎞<br />
1<br />
5<br />
Řešení: Místo s u pro jednoduchost počítejme s û = u/23 = ⎝ 0 ⎠. Jelikož Aû = ⎝ 0 ⎠,<br />
−1<br />
−5<br />
je příslušné vlastní číslo λ 1 = 5.<br />
Charakteristický polynom matice A<br />
(−2 − λ)(3 − λ)(3 − λ) − 28 + 98 − 14(3 − λ) − 14(3 − λ) + 14(−2 − λ)<br />
= (−2 − λ)(9 − 6λ + λ 2 ) + 70 − 84 + 28λ − 28 − 14λ<br />
= −λ 3 + 4λ 2 + 17λ − 60<br />
vydělíme polynomem λ − 5 a dostaneme polynom<br />
−λ 2 − λ + 12 = −(λ − 3)(λ + 4)<br />
s kořeny λ 2 = 3 a λ 3 = −4.<br />
Příslušné vlastní vektory jsou (pozor na jejich (nenulové) násobky komplexním číslem)<br />
⎛ ⎞ ⎛ ⎞<br />
−1<br />
−1<br />
v = ⎝ 1 ⎠ p a w = ⎝ 1 ⎠q, kde p, q ∈ C \ {0}.<br />
1<br />
0<br />
5
Příklad 1.9: Je dána matice A a její vlastní vektor u příslušný jistému neznámému<br />
vlastnímu číslu: ⎛<br />
0 6<br />
⎞<br />
−5<br />
⎛ ⎞<br />
−29<br />
A = ⎝15 9 15⎠, u = ⎝ 0 ⎠.<br />
−6 −6 −1 29<br />
Najděte všechna vlastní čísla matice A a všechny zbývající vlastní vektory matice A.<br />
Dvě pomůcky: a) Vlastní čísla matice A jsou celá čísla.<br />
b) Označíme-li −λ 3 + aλ 2 + bλ + c ≡ det(A − λI), platí a = λ 1 + λ 2 + λ 3 a c = λ 1 λ 2 λ 3 .<br />
Řešení: Vlastní čísla λ 1 = 5, λ 2 = 9 a λ 3 = −6. Hodnoty splňují a) i b).<br />
Příslušné vlastní vektory jsou v = (−1, −2/3, 1) T p a w = (−1, 1, 0) T q, kde p, q ∈<br />
C \ {0}.<br />
Příklad 1.10: Je dána matice A a její vlastní vektor u příslušný jistému neznámému<br />
vlastnímu číslu:<br />
⎛<br />
7 3<br />
⎞<br />
1<br />
⎛ ⎞<br />
−17<br />
A = ⎝−1 3 −1⎠ , u = ⎝ 0 ⎠ p, p ∈ C \ {0}.<br />
−3 −3 3 17<br />
Najděte všechna vlastní čísla matice A a všechny zbývající vlastní vektory matice A.<br />
Řešení: Vlastní čísla λ 1 = 6, λ 2 = 3 a λ 3 = 4.<br />
Příslušné vlastní vektory jsou v = (−1, 1, 1) T p a w = (−1, 1, 0) T q, kde p, q ∈ C \ {0}.<br />
Příklad 1.11: Je dána matice A a její vlastní vektor u příslušný jistému neznámému<br />
vlastnímu číslu: ⎛ ⎞<br />
−3 −1 −11<br />
⎛ ⎞<br />
−43<br />
A = ⎝11 9 11 ⎠ , u = ⎝ 43 ⎠ .<br />
1 1 9 0<br />
Najděte všechna vlastní čísla matice A a všechny zbývající vlastní vektory matice A.<br />
(Dvě kontrolní pomůcky: 1) Vlastní čísla matice A jsou celá čísla. 2) Označíme-li −λ 3 + aλ 2 +<br />
bλ + c ≡ det(A − λI), platí a = λ 1 + λ 2 + λ 3 a c = λ 1 λ 2 λ 3 .)<br />
Řešení: Vlastní čísla λ 1 = −2, λ 2 = 8 a λ 3 = 9.<br />
Příslušné vlastní vektory jsou v = (−1, 0, 1) T p a w = (−1, 1, 1) T q, kde p, q ∈ C \ {0}.<br />
Příklad 1.12: Je dána matice A závislá na parametrech a, b ∈ R a jsou dány vektory u<br />
a v:<br />
⎛<br />
a b<br />
⎞<br />
1<br />
⎛ ⎞<br />
−4<br />
⎛ ⎞<br />
−1<br />
A = ⎝ 5 5 1⎠ , u = ⎝ 5 ⎠ , v = ⎝ 0 ⎠.<br />
−5 −4 0 0 5<br />
Nalezněte takové hodnoty parametrů a, b ∈ R, aby matice A měla vlastní vektory u a v,<br />
stanovte příslušná vlastní čísla. Dále nalezněte zbývající vlastní číslo a zbývající vlastní<br />
vektor matice A (s dosazenými hodnotami parametrů a, b ∈ R).<br />
Řešení: Jelikož<br />
⎛ ⎞<br />
−4a + 5b<br />
⎛ ⎞<br />
−a + 5<br />
Au = ⎝ 5<br />
0<br />
⎠ a Av = ⎝ 0<br />
5<br />
⎠,<br />
6
porovnáním s u a v zjistíme, že vektorům odpovídají vlastní čísla λ 1 = 1 a λ 2 = 1,<br />
a odvodíme rovnice pro parametry a a b:<br />
Odtud a = 6 a b = 4.<br />
Charakteristický polynom 2 matice A<br />
−4a + 5b = −4, −a + 5 = −1.<br />
(6 − λ)(5 − λ)(−λ) − 20 − 20 + 5(5 − λ) + 20λ + 4(6 − λ)<br />
= (−λ)(30 − 11λ + λ 2 ) − 40 + 49 + 11λ = −λ 3 + 11λ 2 − 19λ + 9<br />
vydělíme polynomem (λ − 1) 2 = λ 2 − 2λ + 1 a dostaneme polynom −λ + 9 s kořenem<br />
λ 3 = 9.<br />
Příslušný vlastní vektor (−1, −1, 1) T q, q ∈ C \ {0}.<br />
Příklad 1.13: Je dána matice A závislá na parametrech a, b ∈ R a jsou dány vektory u<br />
a v:<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
3 0 2<br />
−1<br />
−2<br />
A = ⎝−8 −1 −4⎠ , u = ⎝ 2 ⎠ , v = ⎝ 4 ⎠ .<br />
−1 a b 1 1<br />
Nalezněte takové reálné číslo a a takové reálné číslo b, aby vektory u a v byly vlastními<br />
vektory matice A a stanovte příslušná vlastní čísla. Dále nalezněte zbývající vlastní číslo<br />
a zbývající vlastní vektor matice A (s dosazenými hodnotami parametrů a, b ∈ R).<br />
Řešení: Jelikož<br />
⎛<br />
Au = ⎝<br />
−1<br />
2<br />
⎞<br />
⎠ a<br />
⎛<br />
Av = ⎝<br />
−4<br />
8<br />
⎞<br />
⎠ ,<br />
1 + 2a + b<br />
2 + 4a + b<br />
porovnáním s u a v zjistíme, že vektorům odpovídají vlastní čísla λ 1 = 1 a λ 2 = 2,<br />
a odvodíme rovnice pro parametry a a b:<br />
Odtud a = 0 a b = 0.<br />
Charakteristický polynom 3 matice A<br />
1 + 2a + 2b = 1, 2 + 4a + b = 2.<br />
(3 − λ)(−1 − λ)(−λ) − (−1)(−1 − λ)2<br />
= (1 + λ)(−2 + 3λ − λ 2 ) = −λ 3 + 2λ 2 + λ − 2<br />
vydělíme polynomem (λ−1)(λ−2) = λ 2 −3λ+2 a dostaneme polynom −λ−1 s kořenem<br />
λ 3 = −1. Tento kořen lze také snadno najít zkusmým dosazováním do charakteristického<br />
polynomu.<br />
Příslušný vlastní vektor je (0, 1, 0) T q, q ∈ C \ {0}.<br />
2 Jednodušší ovšem je využít toho, že součet vlastních čísel je roven stopě matice, tj. součtu prvků<br />
na hlavní diagonále. Tedy a + 5 = λ 1 + λ 2 + λ 3 , konkrétně 6 + 5 = 1 + 1 + λ 3 . Odtud získáme λ 3 = 9<br />
a vyhneme se zdlouhavému výpočtu charakteristického polynomu.<br />
3 Stejně jako v předchozí úloze je kratší cestou k výsledku vztah 3 − 1 + b = λ 1 + λ 2 + λ 3 .<br />
7
Příklad 1.14: Je dána matice A a její vlastní vektor u příslušný jistému neznámému<br />
vlastnímu číslu:<br />
⎛ ⎞ ⎛ ⎞<br />
a −6 −13<br />
−27<br />
A = ⎝13 8 13 ⎠, u = ⎝ 0 ⎠ p, p ∈ C \ {0},<br />
6 6 8 27<br />
kde a ∈ R. Určete parametr a, najděte všechna vlastní čísla matice A a všechny zbývající<br />
vlastní vektory matice A. (Doporučení: Při výpočtu charakteristického polynomu se snažte<br />
vyhnout vypočítávání součinů. Pracujte se součiny ve tvaru například 6 ·6·13 či 6 ·13 ·13<br />
a ve výrazech vhodně vytýkejte společné činitele.)<br />
Řešení: Počítejme s vlastním vektorem û = (−1, 0, 1) T . Jelikož Aû = (−a − 13, 0, 2) T , je<br />
(dle třetí složky) příslušné vlastní číslo λ 1 = 2 a platí −a − 13 = 2(−1), tedy a = −11.<br />
Charakteristický polynom 4 matice A<br />
(−11 − λ)(8 − λ)(8 − λ) − 6 · 6 · 13 − 6 · 13 · 13<br />
+ 6 · 13(8 − λ) − 6 · 13(−11 − λ) + 6 · 13(8 − λ)<br />
= (−11 − λ)(8 − λ)(8 − λ) − 19 · 6 · 13<br />
+ 6 · 13(8 − λ + 11 + λ + 8 − λ)<br />
= (−11 − λ)(8 − λ)(8 − λ) − 19 · 6 · 13 + 6 · 13(27 − λ) [*]<br />
= (−11 − λ)(64 − 16λ + λ 2 ) + 8 · 6 · 13 − 6 · 13λ<br />
= −11 · 8 · 8 + 11 · 16λ − 11λ 2 − 64λ + 16λ 2 − λ 3 + 8 · 6 · 13 − 6 · 13λ<br />
= 8(78 − 88) + 16λ(11 − 4) + 5λ 2 − λ 3 − 6 · 13λ<br />
= −80 + 2λ(8 · 7 − 3 · 13) + 5λ 2 − λ 3<br />
= −80 + 34λ + 5λ 2 − λ 3<br />
vydělíme polynomem λ − 2 a dostaneme polynom<br />
−λ 2 + 3λ + 40 = −(λ + 5)(λ − 8)<br />
s kořeny λ 2 = 8 a λ 3 = −5.<br />
Příslušné vlastní vektory jsou (pozor na jejich (nenulové) násobky)<br />
v = (−1, 1, 1) T p, p ∈ C \ {0} a w = (−1, 1, 0) T q, q ∈ C \ {0}.<br />
Příklad 1.15: Stanovte hodnotu parametrů a, b ∈ R tak, aby vektor v = (2, 1) T byl<br />
vlastním vektorem matice ( ) a −a<br />
2<br />
A =<br />
b b 2<br />
příslušným některému nenulovému vlastnímu číslu (matice A). Proved’te zkoušku.<br />
Řešení: Necht’ vlastní vektor v odpovídá nějakému vlastnímu číslu λ. Pak platí<br />
−a 2 + 2a = 2λ,<br />
b 2 + 2b = λ.<br />
4 V místě označeném [*] je, jak si povšimli dva studenti, lepší pokračovat takto<br />
a vyhnout se dělení polynomů.<br />
= (−11 − λ)(8 − λ) 2 + 6 · 13(8 − λ) = (8 − λ)[(−11 − λ)(8 − λ) + 78]<br />
= (8 − λ)[−10 + 3λ + λ 2 ] = (8 − λ)(λ − 2)(λ + 5)<br />
8
Jelikož vlastní číslo si můžeme zvolit, volme jednoduše například λ = −1, pak dostáváme<br />
b = −1 a rovnici a 2 − 2a − 2 = 0, jejíž řešení je a 1 = 1 + √ 3 a a 2 = 1 − √ 3.<br />
Vektor v tedy je vlastním vektorem například matice<br />
( √ √ )<br />
1 + 3 −4 − 2 3<br />
A =<br />
.<br />
−1 1<br />
Zkouška — maticí A vynásobíme vektor v, dostaneme vektor −v.<br />
Příklad 1.16: Nalezněte takové hodnoty a, b, c, d ∈ R, aby matice A měla vlastní vektor<br />
v 1 příslušný vlastnímu číslu λ 1 = −4, vlastní vektor v 2 příslušný vlastnímu číslu λ 2 = 5<br />
a vlastní vektor v 3 příslušný vlastnímu číslu λ 3 = 8, přičemž<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 −2 d 1<br />
A = ⎝ a b c⎠ , v 1 = ⎝−2<br />
−2 1 0 1<br />
−2<br />
−2<br />
⎠ , v 2 = ⎝ 1 ⎠ , v 3 = ⎝ 4 ⎠ .<br />
1 1<br />
Řešení: Ze vztahů Av i = λ i v i , i = 1, 2, 3, odvodíme rovnice<br />
a − 2b + c = 8,<br />
−2a + b + c = 5,<br />
−2a + 4b + c = 32,<br />
4 + d = −4, −2 + d = −10, −8 + d = −16.<br />
Dostaneme d = −8. Zbývající soustava maticově<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 −2 1 | 8 1 −2 1 | 8<br />
⎝−2 1 1 | 5 ⎠ ∼ ⎝0 −3 3 | 21⎠.<br />
−2 4 1 | 32 0 3 0 | 27<br />
Odtud b = 9, c = 16, a = 10.<br />
Příklad 1.17: Nalezněte takové hodnoty a, b, c, d ∈ R, aby matice A měla vlastní vektory<br />
v 1 , v 2 a v 3 ; stanovte příslušná vlastní čísla.<br />
⎛ ⎞<br />
a b c<br />
A = ⎝2 7 d⎠ ,<br />
⎛ ⎞<br />
−4<br />
v 1 = ⎝ 1 ⎠ ,<br />
⎛ ⎞<br />
−1<br />
v 2 = ⎝ 1 ⎠ ,<br />
⎛ ⎞<br />
−1<br />
v 3 = ⎝ 1 ⎠ .<br />
4 4 6 4 0 1<br />
Řešení: Označme příslušná vlastní čísla λ 1 , λ 2 , λ 3 . Ze vztahů Av i = λ i v i , i = 1, 2, 3,<br />
porovnáním třetích složek vektorů zjistíme, že λ 1 = 3 a λ 3 = 6, z porovnání druhé složky<br />
plyne λ 2 = 5. Nyní z Av i = λ i v i odvodíme rovnice<br />
−4a + b + 4c = −12,<br />
−a + b = −5,<br />
−a + b + c = −6<br />
a přímo d = 1, dále pak a = 1, b = −4 a c = −1.<br />
9
Příklad 1.18: Nalezněte takové hodnoty a, b, c, d ∈ R, aby matice A měla vlastní vektory<br />
v 1 , v 2 a v 3 , přičemž<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
a b c<br />
−2 2 4<br />
A = ⎝20 10 44⎠, v 1 = ⎝ 2 ⎠ , v 2 = ⎝−2⎠ , v 3 = ⎝−2⎠ .<br />
−2 d 12 0<br />
−1<br />
−2<br />
Zkouškou ověřte, že nalezené hodnoty vyhovují zadání úlohy.<br />
Řešení: a = −6, b = 4, c = −44 a d = −2.<br />
Zkouškou násobením ověříme, že matice<br />
⎛ ⎞ ⎛ ⎞<br />
−6 4 −44 −3 2 −22<br />
A = ⎝20 10 44 ⎠ = 2 ⎝10 5 22 ⎠<br />
−2 −2 12 −1 −1 6<br />
má vlastní vektory<br />
⎛ ⎞<br />
−1<br />
⎛ ⎞<br />
2<br />
⎛ ⎞<br />
2<br />
v 1 = ⎝ 1 ⎠ , v 2 = ⎝−2⎠ , v 3 = ⎝−1⎠ .<br />
0<br />
−1<br />
−1<br />
Příklad 1.19: Nalezněte čtveřici takových hodnot a, b, c, d ∈ R, aby matice A měla vlastní<br />
vektor v 1 příslušný vlastnímu číslu λ 1 = −5, vlastní vektor v 2 příslušný vlastnímu číslu<br />
λ 2 = 6 a vlastní vektor v 3 příslušný vlastnímu číslu λ 3 = 7, přičemž<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
a b c<br />
−1<br />
−2<br />
−2<br />
A = ⎝10 5 22⎠ , v 1 = ⎝ 1 ⎠ , v 2 = ⎝ 2 ⎠, v 3 = ⎝ 1 ⎠ .<br />
−1 d 6 0 1 1<br />
Řešení: a = −3, b = 2, c = −22 a d = −1.<br />
Příklad 1.20: Nalezněte všechny hodnoty parametru a ∈ R takové, aby ‖A‖ 2 = 1, kde<br />
( )<br />
2a 0<br />
A = .<br />
a a<br />
Řešení: Matice A není symetrická, tedy ‖A‖ 2 = √ ρ(A T A). Jest<br />
( ) ( ) ( )<br />
2 1 2 0 5 1<br />
A T A = a 2 = a 2 ≡ a 2 C, kde C =<br />
0 1 1 1 1 1<br />
( ) 5 1<br />
.<br />
1 1<br />
Tedy 1 = ‖A‖ 2 = √ ρ(a 2 C) = √ a 2 ρ(C) = |a| √ ρ(C), odtud |a| = 1/ √ ρ(C).<br />
Vlastní čísla matice C: Charakteristický polynom<br />
det(C − λI) = (5 − λ)(1 − λ) − 1 = λ 2 − 6λ + 4<br />
s kořeny<br />
λ 1,2 = 6 ± √ 36 − 16<br />
2<br />
10<br />
= 3 ± √ 5.
Tudíž √ ρ(C) = √ 3 + √ 5 a<br />
a =<br />
1<br />
1<br />
√ √ spolu s a = −√ √<br />
3 + 5 3 + 5<br />
jsou hledané hodnoty parametru a.<br />
Studenti budou pravděpodobně hledat vlastní čísla matice a 2 C, její charakteristický<br />
polynom je λ 2 − 6a 2 λ + 4a 4 , jeho kořeny 3a 2 ± a 2√ 5.<br />
Příklad 1.21: Je dána matice A a vektory u, v:<br />
( ) a b<br />
A = , u =<br />
c 3<br />
( 1<br />
1)<br />
, v =<br />
( 2<br />
1)<br />
.<br />
Výpočtem nalezněte takové hodnoty parametrů a, b, c ∈ R a čísel λ u , λ v ∈ R, aby zároveň<br />
platilo:<br />
(i) u je vlastní vektor matice A příslušný číslu λ u ∈ R a v je vlastní vektor matice A<br />
příslušný číslu λ v ∈ R;<br />
(ii) číslo λ v je o dvě větší než číslo λ u .<br />
Proved’te zkoušku správnosti řešení.<br />
Připomenutí: Platí, že součet hodnot vlastních čísel je roven součtu těch prvků matice,<br />
které leží na hlavní diagonále.<br />
Doporučení: Budete-li řešit soustavu rovnic, rovnice si nejprve vhodně uspořádejte.<br />
Uklidnění: Případný nadbytek rovnic nemusí být na závadu.<br />
Upozornění: Nebudou tolerovány numerické chyby, protože zkouška správnosti řešení je<br />
velmi snadná a rychlá.<br />
Řešení: Z rovností Au = λ u , Av = λ v , požadavku (ii) a připomenutí dostáváme<br />
a + b = λ u ,<br />
c + 3 = λ u ,<br />
2a + b = 2λ v ,<br />
2c + 3 = λ v ,<br />
λ v − λ u = 2,<br />
λ u + λ v = 3 + a,<br />
}<br />
=⇒<br />
a + b − λ u = 0,<br />
c − λ u = −3,<br />
2a + b − 2λ v = 0,<br />
2c − λ v = −3,<br />
−λ u + λ v = 2,<br />
a − λ u − λ v = −3,<br />
}<br />
=⇒<br />
a + b − λ u = 0,<br />
2a + b − 2λ v = 0,<br />
a − λ u − λ v = −3,<br />
c − λ u = −3,<br />
2c − λ v = −3,<br />
−λ u + λ v = 2.<br />
11
Maticově<br />
⎛<br />
1 1 0 −1 0 |<br />
⎞<br />
0<br />
⎛<br />
1 1 0 −1 0 |<br />
⎞<br />
0<br />
2 1 0 0 −2 | 0<br />
0 −1 0 2 −2 | 0<br />
1 0 0 −1 −1 | −3<br />
⎜0 0 1 −1 0 | −3<br />
∼<br />
0 −1 0 0 −1 | −3<br />
⎟ ⎜0 0 1 −1 0 | −3<br />
⎟<br />
⎝0 0 2 0 −1 | −3⎠<br />
⎝0 0 0 2 −1 | 3 ⎠<br />
0 0 0 −1 1 | 2 0 0 0 −1 1 | 2<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 1 0 −1 0 | 0 1 1 0 −1 0 | 0<br />
0 −1 0 2 −2 | 0<br />
0 −1 0 2 −2 | 0<br />
∼<br />
0 0 0 −2 1 | −3<br />
⎜0 0 1 −1 0 | −3<br />
∼<br />
0 0 1 −1 0 | −3<br />
⎟ ⎜0 0 0 1 −1 | −2<br />
⎟<br />
⎝0 0 0 0 1 | 7 ⎠ ⎝0 0 0 −2 1 | −3⎠<br />
0 0 0 −1 1 | 2 0 0 0 0 1 | 7<br />
⎛<br />
⎞<br />
1 1 0 −1 0 | 0 ⎛<br />
⎞<br />
0 −1 0 2 −2 | 0<br />
1 1 0 −1 0 | 0<br />
∼<br />
0 0 1 −1 0 | −3<br />
0 −1 0 2 −2 | 0<br />
⎜0 0 0 1 −1 | −2<br />
∼<br />
⎜0 0 1 −1 0 | −3<br />
⎟<br />
⎟ ⎝<br />
⎝0 0 0 0 −1 | −7⎠<br />
0 0 0 1 −1 | −2⎠ 0 0 0 0 1 | 7<br />
0 0 0 0 1 | 7<br />
Odtud λ v = 7, λ u = 5, c = 2, b = −4 a a = 9.<br />
Zkouška ( ) ( ( ( ) (<br />
9 −4 1 5 9 −4 2<br />
= ,<br />
=<br />
2 3 1)<br />
5)<br />
2 3 1)<br />
( )<br />
14<br />
.<br />
7<br />
Příklad 1.22: Jsou dány tyto matice<br />
( ) ( )<br />
1 0<br />
−1 −1<br />
I = , A =<br />
0 1<br />
−1 −1<br />
Spočtěte<br />
a) vlastní čísla matice B;<br />
b) ‖B‖ 2 ;<br />
c) vlastní čísla matice 17I − B.<br />
, B = A 5 = AAAAA.<br />
Řešení: a) Standardním postupem s vyřešením charakteristické rovnice se snadno spočítá,<br />
že matice A má vlastní čísla λ 1 = 0 a λ 2 = −2. Ještě rychlejší však je tato úvaha: Matice<br />
A je singulární, má tedy vlastní číslo λ 1 = 0. Jelikož dále obecně platí λ 1 + λ 2 = −1 − 1,<br />
dostáváme λ 2 = −2.<br />
b) Matice B má vlastní čísla µ 1 = 0 a µ 2 = (−2) 5 = −32 a je symetrická, tedy<br />
‖B‖ 2 = 32.<br />
c) Zaved’me matici C ≡ 17I − B. Jestliže θ je vlastní číslo matice C a v příslušný<br />
vlastní vektor, pak θv = Cv = (17I − B)v = 17v − Bv, odtud Bv = (17 − θ)v, což<br />
znamená, že v je také vlastním vektorem matice B příslušným vlastnímu číslu 17 − θ.<br />
Ještě snáze nahlédneme, že pokud µ je vlastní číslo matice B a w příslušný vlastní vektor,<br />
tj. µw = Bw, pak Cw = 17w − Bw = (17 − µ)w, a tudíž w je vlastní vektor matice C<br />
příslušný vlastnímu číslu θ = 17 − µ.<br />
12
Ověřili jsme tedy, že matice C a B mají totožný systém vlastních vektorů a odvodili<br />
jsme vztah mezi odpovídajícími vlastními čísly, tj. θ = 17 −µ. Jelikož µ 1 = 0 a µ 2 = −32,<br />
vlastní čísla matice 17I − B jsou θ 1 = 17 a θ 2 = 49.<br />
Příklad 1.23: Je dána matice A a její vlastní vektory u a v:<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
−1 4 4<br />
−1 0<br />
A = ⎝ 8 −8 −14⎠ , u = ⎝−2⎠ , v = ⎝−1⎠ .<br />
−4 7 13 1 1<br />
Určete všechna vlastní čísla matice a třetí vlastní vektor matice A (nezapomeňte na<br />
násobky). Označte w ten třetí vlastní vektor matice A, jehož první složka má hodnotu 2,<br />
a vypočítejte vektor B(w + u), kde matice B = AA. (Poznámka: Součet vlastních čísel<br />
matice je roven stopě matice, tj. součtu prvků ležících na hlavní diagonále matice.)<br />
Řešení: První složka součinu Au je rovna −3, vlastní číslo λ 1 = 3. Druhá složka součinu<br />
Av je rovna −6, vlastní číslo λ 2 = 6. Jest λ 3 = trA − λ 1 − λ 2 = 4 − 9 = −5.<br />
Zbývající vlastní vektor přísluší vlastnímu číslu λ 3 = −5 a je řešením soustavy s nulovou<br />
pravou stranou (soustava vznikne z matice A + 5I)<br />
⎛ ⎞ ⎛ ⎞<br />
4 4 4 1 1 1 ( )<br />
⎝ 8 −3 −14⎠ ∼ ⎝0 −11 −22⎠ 1 1 1<br />
∼ .<br />
0 1 2<br />
−4 7 18 0 11 22<br />
⎛ ⎞<br />
⎛ ⎞<br />
1<br />
2<br />
Vlastní vektor a jeho násobky z = ⎝−2⎠ p, p ∈ C \ {0}. Vektor w = ⎝−4⎠.<br />
1<br />
⎛ ⎞<br />
2<br />
⎛ ⎞<br />
50 − 9 41<br />
Jest B(w + u) = AAw + AAu = λ 2 3w + λ 2 1u = 25w + 9u = ⎝−100 − 18⎠ = ⎝−118⎠.<br />
50 + 9 59<br />
2 Aplikace Geršgorinovy věty: vlastní čísla matic<br />
Příklad 2.1: Je dána matice<br />
⎛<br />
⎞<br />
−2 1/2 + i −i/2 0<br />
A = ⎜ 1 − i − √ 3 − √ √ √<br />
√<br />
6i 0 2 + 2i<br />
√ ⎟<br />
⎝ 2i 0 3 − 7i 1 + i<br />
1 − 2i 1/2 i/2 − √ 7 + 3 √ ⎠ .<br />
2i<br />
Pomocí Geršgorinovy věty zjistěte,<br />
a) zda by číslo 2 + 2i mohlo být vlastním číslem matice A;<br />
b) zda by číslo −1 − i mohlo být vlastním číslem matice A.<br />
Odpovědi jasně zformulujte a zdůvodněte.<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice A v množině M, která<br />
je sjednocením kruhů K i se středy S i a poloměry r i , i = 1, 2, 3, 4, tj.<br />
K 1 = {z ∈ C : | − 2 − z| ≤ r 1 }, kde r 1 = √ 5/2 + 1/2,<br />
K 2 = {z ∈ C : | − √ 3 − √ 6i − z| ≤ r 2 }, kde r 2 = √ 2 + 2,<br />
K 3 = {z ∈ C : |3 − √ 7i − z| ≤ r 3 }, kde r 3 = √ 2 + √ 2,<br />
K 4 = {z ∈ C : | − √ 7 + 3 √ 2i − z| ≤ r 4 }, kde r 4 = √ 5 + 1/2 + 1/2 = 1 + √ 5.<br />
13
6<br />
S_4<br />
4<br />
2 B_1<br />
S_1<br />
K4 K2 0 2 4<br />
B_2K2<br />
S_2 S_3<br />
K4<br />
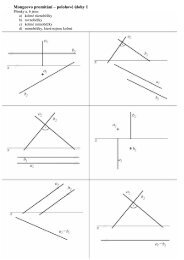
Z obrázku vidíme, že<br />
a) 2+2i (viz bod B 1 ) neleží v množině M, takže<br />
nemůže být vlastním číslem matice A.<br />
b) −1 − i (viz bod B 2 ) leží v množině M, takže<br />
není vyloučeno, že je vlastním číslem matice A.<br />
Obrázek je zde vyroben vhodným softwarem,<br />
tedy je poměrně přesný. Náčrtek od ruky by však<br />
pro odpověd’ nebyl dostatečným zdůvodněním.<br />
Proto je vhodné pozorování a) a b) potvrdit<br />
výpočtem.<br />
Označme d j i vzdálenost bodu B j od bodu S i , kde i = 1, 2, 3, 4 a j = 1, 2. Platí<br />
d 1 1 = |2 + 2i − (−2)| = |4 + 2i| > 4 > r 1 ,<br />
d 1 2 = |2 + 2i − (−√ 3 − √ 6i)| > |2 + √ 3| > r 2 ,<br />
d 1 3 = |2 + 2i − (3 − √ 7i)| = | − 1 + (2 + √ 7)i| > 2 + √ 7 > 4 > r 3 ,<br />
d 1 4 = |2 + 2i − (−√ 7 + 3 √ 2i)| > |2 + √ 7| > 4 > r 4 ,<br />
d 2 2 = | − 1 − i − (−√ 3 − √ 6i)| = | √ 3 − 1 + ( √ 6 − 1)i|<br />
( )<br />
∣ <<br />
5<br />
∣ 2 − 1 + 2 − 1 ∣∣∣<br />
i<br />
∣ = 1 + 3 ∣ ∣∣∣<br />
2 i = √ 13/4 < 2 < r 2 .<br />
První čtyři řádky dokazují, že bod B 1 leží mimo množinu M, pátý řádek ukazuje, že bod<br />
B 2 leží v kruhu K 2 .<br />
Příklad 2.2: Je dána matice<br />
⎛√ √ √<br />
5 + 11 i −1/4 − 15i/4 3i/4<br />
⎞ −1/2 − i<br />
A = ⎜ i 3 − 4i 1/2 − i/2 1/3 + i/3<br />
⎝ 1 + 2i i/2 −4 − √ ⎟<br />
11i −1/2 ⎠ .<br />
2 − i 1 + i −1 −6<br />
Pomocí Geršgorinovy věty zjistěte,<br />
a) zda by číslo 1/2 + i/2 mohlo být vlastním číslem matice A;<br />
b) zda by číslo 1 − i mohlo být vlastním číslem matice A.<br />
Odpovědi jasně zformulujte a zdůvodněte.<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice C v množině M, která<br />
je sjednocením kruhů K i se středy S i a poloměry r i , i = 1, 2, 3, 4, tj.<br />
K 1 = {z ∈ C : | √ 5 + √ 11i − z| ≤ 1 + 3/4 + √ 5/2 = 7/4 + √ 5/2},<br />
K 2 = {z ∈ C : |3 − 4i − z| ≤ 1 + √ 2/2 + √ 2/3},<br />
K 3 = {z ∈ C : | − 4 − √ 11i − z| ≤ √ 5 + 1/2 + 1/2 = 1 + √ 5},<br />
K 4 = {z ∈ C : | − 6 − z| ≤ √ 5 + √ 2 + 1}.<br />
14
6<br />
4<br />
S_1<br />
2<br />
S_4<br />
L_1<br />
K10 K5 0 5<br />
L_2<br />
K2<br />
S_3<br />
K4<br />
S_2<br />
K6<br />
Odtud vidíme, že<br />
a) 1/2 + i/2 neleží v množině M, takže<br />
nemůže být vlastním číslem matice A.<br />
b) 1 − i neleží v množině M, takže<br />
nemůže být vlastním číslem matice A.<br />
Obrázek je zde vyroben vhodným softwarem,<br />
tedy je poměrně přesný. Náčrtek<br />
od ruky by však pro odpověd’ nebyl<br />
dostatečným zdůvodněním. Proto<br />
je vhodné pozorování a) a b) potvrdit<br />
výpočtem.<br />
Označme d j i vzdálenost bodu L j od bodu S i , kde i = 1, 2, 3, 4 a j = 1, 2. Platí<br />
d 1 1 = |1/2 + i/2 − ( √ 5 + √ 11i)| = |1/2 − √ 5 + (1/2 − √ 11)i|<br />
√<br />
= (1/2 − √ 5) 2 + (1/2 − √ √<br />
11) 2 = 1/4 − √ 5 + 5 + 1/4 − √ 11 + 11<br />
√<br />
= 16 + 1/2 − √ 5 − √ 11 > √ 16 + 1/2 − 3 − 4 = √ 9 + 1/2 > 3<br />
= 5/4 + 7/4 = ( √ 5/2)( √ 5/2) + 7/4 > (2/2)( √ 5/2) + 7/4 = √ 5/2 + 7/4 = r 1 ,<br />
d 1 2 = |1/2 + i/2 − (3 − 4i)| = | − 5/2 + 9i/2| > 9/2 > r 2,<br />
d 1 3 = |1/2 + i/2 − (−4 − √ 11i)| = |9/2 + (1/2 + √ 11)i| > 9/2 > r 3 ,<br />
d 1 4 = |1/2 + i/2 − (−6)| = |13/2 + i/2| > 13/2 > r 4 ,<br />
d 2 1 = |1 − i − ( √ 5 + √ 11i)| = |1 − √ 5 − (1 + √ 11)i| > | − (1 + √ 11)i|<br />
= 1 + √ 11 > 1 + 3 = 4 > r 1 ,<br />
d 2 2 = |1 − i − (3 − 4i)| = | − 2 + 3i| = √ 13 > 3 > r 2 ,<br />
d 2 3 = |1 − i − (−4 − √ 11i)| = |5 + ( √ 11 − 1)i| > 5 > r 3 ,<br />
d 2 4 = |1 − i − (−6)| = |7 − i| > 7 > r 4 .<br />
První čtyři řetězce rovností a nerovností dokazují, že bod L 1 leží mimo množinu M, zbývající<br />
rovnosti a nerovnosti ukazují, že také bod L 2 leží mimo množinu M.<br />
Příklad 2.3: Rozhodněte, zda na základě Geršgorinovy věty můžete tvrdit, že<br />
a) λ 1 = −4i, b) λ 2 = 5 + i je či není vlastní číslo matice A, kde<br />
⎛<br />
⎞<br />
3 + 2i 0 1 1 + i<br />
1<br />
A = ⎜ 2<br />
−4 + i 0 −2<br />
⎝ 1<br />
1<br />
9 − 1 3 i 5 1<br />
⎟<br />
⎠ .<br />
3<br />
0<br />
2<br />
− 1 2<br />
2 − 3i<br />
c) Je matice A regulární<br />
d) Může být číslo λ 3 = − 1 + 3i vlastním číslem matice A −1 <br />
10<br />
Zformulujte odpovědi a své závěry zdůvodněte.<br />
Řešení: Podle Geršgorinovy věty (viz [4]) leží všechna vlastní čísla matice A v množině M, která<br />
15
je sjednocením kruhů K i se středy S i a poloměry r i , i = 1,2,3,4, tj.<br />
S_2<br />
K 1 = {z ∈ C : |3 + 2i − z| ≤ 1 + |1 + i| = 1 + √ 2},<br />
K 2 = {z ∈ C : | − 4 + i − z| ≤ 1/2 + | − 2| = 5/2},<br />
K 3 = {z ∈ C : |5 − z| ≤ 1 + |1/9 − i/3| + 1 = 2 + √ 10/9},<br />
K 4 = {z ∈ C : |2 − 3i − z| ≤ 3/2 + | − 1/2| = 2}.<br />
4<br />
L_4<br />
3<br />
2<br />
1<br />
K4<br />
L_1<br />
S_1<br />
L_2<br />
K6 K4 K2 0 2 4 S_3 6<br />
K1<br />
K2<br />
K3<br />
S_4<br />
Z obrázku vidíme, že<br />
a) −4i (viz bod L 1 ) neleží v množině<br />
M, takže nemůže být vlastním číslem<br />
matice A.<br />
b) 5+i (viz bod L 2 ) leží v množině M,<br />
takže není vyloučeno, že je vlastním<br />
číslem matice A. Není tím ovšem<br />
zaručeno, že λ 2 je vlastním číslem.<br />
c) Matice je singulární právě tehdy,<br />
když 0 ≡ 0 + 0i je jejím vlastním<br />
číslem. Počátek souřadnic však leží<br />
mimo sjednocení kruhů, matice A<br />
tudíž je regulární.<br />
d) Z c) víme, že existuje inverzní matice A −1 . Vlastní čísla matice A −1 jsou převrácenými<br />
hodnotami vlastních čísel matice A. Výpočtem zjistíme, že<br />
λ 4 ≡ 1 = − 10 = −1 + 3i.<br />
λ 3 1 + 3i<br />
Číslo λ 4 (viz bod L 4 ) leží mimo kruhy, není vlastním číslem matice A, tudíž ani číslo λ 3 není<br />
vlastním číslem matice A −1 .<br />
Obrázek je zde vyroben vhodným softwarem, tedy je poměrně přesný. Náčrtek od ruky by<br />
však pro odpověd’ nebyl dostatečným zdůvodněním. Proto je vhodné pozorování a) a b) potvrdit<br />
výpočtem.<br />
Označme d j i vzdálenost bodu L j od bodu S i , kde i = 1,2,3,4 a j = 1,2,4. Platí<br />
d 1 1 = | − 4i − (3 + 2i)| = | − 3 − 6i| > 6 > r 1,<br />
d 1 2 = | − 4i − (−4 + i)| = |4 − 5i| > 5 > r 2 ,<br />
d 1 3 = | − 4i − 5| > 5 > r 3,<br />
d 1 4 = | − 4i − (2 − 3i)| = | − 2 − i| = √ 5 > r 4 ,<br />
d 2 3 = |5 + i − 5| = |i| = 1 < r 3 ,<br />
d 4 1 = | − 1 + 3i − (3 + 2i)| = | − 4 + i| > 4 > r 1,<br />
d 4 2 = | − 1 + 3i − (−4 + i)| = |3 + 2i| > 3 > r 2 ,<br />
d 4 3 = | − 1 + 3i − 5| = | − 6 + 3i| > 6 > r 3 ,<br />
d 4 4 = | − 1 + 3i − (2 − 3i)| = | − 3 + 6i| > 6 > r 4.<br />
První čtyři řádky dokazují, že bod L 1 leží mimo množinu M, pátý řádek ukazuje, že bod L 2 leží<br />
v kruhu K 3 , poslední čtyři řádky dokládají, že bod L 4 leží mimo množinu M.<br />
Příklad 2.4: Je dána matice<br />
⎛<br />
⎞<br />
6 − i −1/4 − i/3 −1/5 + i/4 0 1/2 − i/10<br />
−1 − i 4 + 5i −i/2 2/3 − i/7 −1/2 + i/2<br />
A =<br />
⎜ 1/6 1 + i/2 −3 + 6i 1/2 + 3i/4 0<br />
⎟<br />
⎝ 1/2 −i/4 0 −5 −i/5<br />
1/2 + √ ⎠ .<br />
3i/2 −i/3 1/9 − i/4 1/6 0<br />
16
Pomocí Geršgorinovy věty zjistěte,<br />
a) zda by číslo −1/ √ 2 + i/ √ 2 mohlo být vlastním číslem matice A;<br />
b) zda by číslo −1 − 3i mohlo být vlastním číslem matice A;<br />
c) zda by číslo 1 − 3i mohlo být vlastním číslem matice A.<br />
Odpovědi jasně zformulujte a zdůvodněte.<br />
Řešení:<br />
S_3<br />
8<br />
6<br />
S_2<br />
4<br />
2<br />
L_1 S_5<br />
S_4 K4 K2 0 2 4 6<br />
S_1<br />
K2<br />
L_2 L_3<br />
Podle Geršgorinovy věty leží všechna vlastní<br />
čísla matice C v množině M, která je sjednocením<br />
kruhů se středy [6, −1], [4,5], [−3,6],<br />
[−5,0] a s odpovídajícími poloměry menšími než<br />
2, 4, 3, 1 a kruhu se středem [0,0] s poloměrem<br />
větším než 1, ale menším než 2. Poloměry stačí<br />
takto odhadnout, není třeba je přesně spočítat.<br />
Porovnáním poloměrů kruhů (jejich odhadů) se<br />
vzdálenostmi mezi zkoumanými body a středy<br />
kruhů odvodíme, že a) mohlo, b) nemohlo, c)<br />
nemohlo.<br />
Příklad 2.5: Je dána matice<br />
⎛<br />
⎞<br />
−1 + 3i 1/2 + i −i/4 1/(1 + i)<br />
A = ⎜(1 − i)/2 − √ 7 − √ 6i i/2 1 + √ √<br />
2i<br />
√ ⎟<br />
⎝ 2i 0 3 − 2 2i 2/(2 + i)<br />
1 − 2i 1/2 i/2 − √ 7 + 3 √ ⎠ .<br />
2i<br />
Pomocí Geršgorinovy věty zjistěte,<br />
a) zda je zaručeno, že matice A je regulární;<br />
b) zda by číslo λ 1 = 2 + 2i mohlo být vlastním číslem matice A;<br />
c) zda by číslo λ 2 = −2 + 3i mohlo být vlastním číslem matice A;<br />
d) zda by číslo λ 3 = 1/5 − i/10 mohlo být vlastním číslem matice A −1 .<br />
Odpovědi jasně zformulujte a zdůvodněte.<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice C v množině M, která je<br />
sjednocením kruhů<br />
K 1 = {z ∈ C : | − 1 + 3i − z| ≤ √ 5/2 + 1/4 + √ 2/2},<br />
K 2 = {z ∈ C : | − √ 7 − √ 6i − z| ≤ √ 2/2 + 1/2 + √ 3},<br />
K 3 = {z ∈ C : |3 − 2 √ 2i − z| ≤ √ 2 + 2 √ 5/5},<br />
K 4 = {z ∈ C : | − √ 7 + 3 √ 2i − z| ≤ √ 5 + 1}.<br />
17
6 Odtud vidíme, že<br />
a) 0 + 0i neleží v množině M, matice A je tedy regulární.<br />
S_4<br />
4<br />
S_1<br />
b) 2+2i (bod L 1 ) neleží v množině M, takže nemůže<br />
být vlastním číslem matice A.<br />
L_2<br />
2<br />
c) −2 + 3i (bod L 2 )leží v množině M, takže není vyloučeno,<br />
že je vlastním číslem matice A.<br />
L_1 L_4<br />
d) λ 3 je vlastním číslem matice A −1 právě tehdy, je-li<br />
K4 K2 0 2 4 λ 4 = 4 + 2i vlastním číslem matice A; λ 4 (bod L 4 )<br />
však neleží v M, tudíž 1/5−i/10 určitě není vlastním<br />
K2<br />
číslem matice A −1 .<br />
S_2<br />
S_3 Tyto závěry je třeba podpořit výpočty a odhady jako<br />
K4<br />
v Příkladě 2.3.<br />
Příklad 2.6: Je dána matice<br />
⎛<br />
⎞<br />
1 + 3i 1 + i 2/(1 + i)<br />
A = ⎝ 1/2 3 − 2i (1 + i)/i⎠ .<br />
−2i (1 + i)/2 −3i<br />
Pomocí Geršgorinovy věty zjistěte,<br />
a) zda je zaručeno, že matice A je regulární;<br />
b) zda by číslo 2 + 3i mohlo být vlastním číslem matice A;<br />
c) zda by číslo −3 − 2i mohlo být vlastním číslem matice A;<br />
d) zda by číslo −2/5 − i/5 mohlo být vlastním číslem matice A −1 .<br />
Odpovědi jasně zformulujte a zdůvodněte. Pomůcka: √ 2 = 1,41.<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice A v množině M, která je<br />
sjednocením kruhů<br />
K 1 = {z ∈ C : |1 + 3i − z| ≤ √ 2 + √ 2},<br />
K 2 = {z ∈ C : |3 − 2i − z| ≤ 1/2 + √ 2},<br />
K 3 = {z ∈ C : | − 3i − z| ≤ 2 + √ 2/2}.<br />
4<br />
S_1 L_1<br />
2<br />
L_4<br />
K3 K2 K1 0 1 2 3 4<br />
K2<br />
L_2<br />
S_2<br />
S_3<br />
K4<br />
Vidíme, že<br />
a) 0 + 0i neleží v množině M, matice A je tedy regulární.<br />
b) 2+3i (bod L 1 ) leží v množině M, takže není vyloučeno,<br />
že je vlastním číslem matice A.<br />
c) −3−2i (bod L 2 )neleží v množině M, takže nemůže být<br />
vlastním číslem matice A.<br />
d) −2/5 −i/5 je vlastním číslem matice A −1 právě tehdy,<br />
je-li −2+i vlastním číslem matice A; −2+i (bod L 4 ) však<br />
neleží v M.<br />
Tato pozorování je však třeba dokázat výpočty a odhady<br />
jako v Příkladě 2.3.<br />
18
⎛<br />
10/(1 − 3i) 2/(1 − i)<br />
⎞<br />
1 − i<br />
Příklad 2.7: Je dána matice A = ⎝ −1/4 (4 + 2i)/(1 + i) 1 − i ⎠. Pomocí Geršgorinovy<br />
−i (1 + i)/2 1 − 2i<br />
věty zjistěte,<br />
a) zda je zaručeno, že matice A je regulární;<br />
b) zda by číslo 2 − 3i/2 mohlo být vlastním číslem matice A;<br />
c) zda by číslo −1 − 2i mohlo být vlastním číslem matice A;<br />
d) zda by číslo −2/13 − 3i/13 mohlo být vlastním číslem matice A −1 .<br />
Odpovědi jasně zformulujte a zdůvodněte (ke zdůvodnění nestačí hrubý náčrtek, ale je nutné<br />
odpověd’ podpořit výpočtem nebo logickou úvahou).<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice A v množině M, která je<br />
sjednocením kruhů<br />
K 1 = {z ∈ C : |1 + 3i − z| ≤ √ 2 + √ 2},<br />
K 2 = {z ∈ C : |3 − i − z| ≤ 1/4 + √ 2},<br />
K 3 = {z ∈ C : |1 − 2i − z| ≤ 1 + √ 2/2}.<br />
5<br />
4<br />
L_4<br />
3<br />
2<br />
S_1<br />
1<br />
K2 K1 0 1 2 3 4<br />
K1<br />
S_2<br />
K2 L_1<br />
L_2 S_3<br />
K3<br />
Díky pečlivě narýsovanému obrázku vidíme, že<br />
a) 0 + 0i neleží v množině M, matice A je tedy regulární.<br />
b) 2 − 3i/2 (bod L 1 ) leží v množině M, takže není vyloučeno,<br />
že je vlastním číslem matice A.<br />
c) −1 − 2i (bod L 2 ) neleží v množině M, takže nemůže<br />
být vlastním číslem matice A (vzdálenost bodu od středu<br />
kruhu K 3 je 2, je tedy větší než jeho poloměr 1 + √ 2/2<br />
(proč platí tato nerovnost).<br />
d) −2/13 − 3i/13 je vlastním číslem matice A −1 právě<br />
tehdy, je-li −2 + 3i vlastním číslem matice A; −2 + 3i<br />
(bod L 4 ) však neleží v M.<br />
Tato pozorování je nutné potvrdit výpočty, protože body<br />
L 2 a L 4 leží v blízkosti kruhů. Platí však například, že<br />
vzdálenost L 4 od S 1 je rovna 3, ale poloměr r 1 kruhu K 1<br />
je menší než 3, nebot’ r 2 1 = 4 · 2 = 8 < 9 = 32 .<br />
⎛<br />
√ ⎞ 2<br />
a −3 + 4i<br />
1 − i<br />
Příklad 2.8: Je dána matice A = ⎜25 − 15i<br />
⎟ závislá na komplexním<br />
⎝ 9 + 3i 0<br />
1 + 3i<br />
0 1 − √ ⎠<br />
√ √<br />
3i 3 − 2i<br />
parametru a.<br />
Pomocí Geršgorinovy věty zjistěte, zda lze najít takovou hodnotu parametru a ∈ C, aby<br />
bylo zaručeno, že číslo 18 + 3i není vlastním číslem matice A. Pokud taková hodnota existuje,<br />
uved’te ji (je-li jich více, stačí uvést jednu).<br />
Dosad’te a ≡ 1 + 6i a pomocí Geršgorinovy věty zjistěte,<br />
a) zda by číslo −4 − 2i mohlo být vlastním číslem matice A;<br />
b) zda je zaručeno, že matice A je regulární, a pokud je regulární, zda číslo 1<br />
10 − i může být<br />
30<br />
vlastním číslem matice A −1 .<br />
19
Odpovědi jasně zformulujte a zdůvodněte (ke zdůvodnění nestačí náčrtek, ale je nutné odpověd’<br />
podpořit výpočtem a logickou úvahou). Poznámka: V uvedených komplexních číslech se<br />
odmocňují pouze reálná čísla, nikoli imaginární jednotka i.<br />
Řešení: Podle Geršgorinovy věty leží všechna vlastní čísla matice A v množině M, která je<br />
sjednocením kruhů<br />
{<br />
√ 2 1 + i<br />
K 1 = z ∈ C : |a − z| ≤ | − 3 + 4i| +<br />
∣1 − i 1 + i∣<br />
= 5 + √ 2<br />
1 + i<br />
∣ 2 ∣<br />
}, = 5 + 1 = 6<br />
{<br />
∣ K 2 = z ∈ C : |9 + 3i − z| ≤<br />
25 − 15i 1 − 3i<br />
∣∣∣ ∣ 1 + 3i 1 − 3i∣ = 5 − 15i − 3i + 9i2<br />
5 10 ∣<br />
= | − 2 − 9i| = √ }<br />
85 ,<br />
K 3 = {z ∈ C : | √ 3 − √ 2i − z| ≤ |1 − √ 3i| = 2}.<br />
Číslo 18 + 3i leží v K 2 (nebot’ |9 + 3i − (18 + 3i)| = 9 < √ 85), a at’ tedy zvolíme a jakkoli,<br />
nemůžeme zaručit, že 18 + 3i není vlastním číslem matice A.<br />
a) Jelikož<br />
|1 + 6i − (−4 − 2i)| = |5 + 8i| = √ 89 > 6,<br />
|9 + 3i − (−4 − 2i)| = |13 + 5i| > 13 > √ 85,<br />
| √ 3 − √ 2i − (−4 − 2i)| = | √ 3 + 4 + (2 − √ 2)i| > |4| > 2,<br />
bod −4 − 2i neleží v žádném z kruhů, tudíž nemůže být vlastním číslem matice A.<br />
b) Jelikož<br />
|1 + 6i| = √ 37 > 6,<br />
|9 + 3i| = √ 90 > √ 85,<br />
| √ 3 − √ 2i| = | √ 5| > 2,<br />
bod 0 + 0i neleží v žádném z kruhů, tudíž nemůže být vlastním číslem matice A. Matice A tedy<br />
je regulární.<br />
Číslo ˜λ = 1 10 − i<br />
30 je vlastním číslem matice A−1 právě tehdy, když číslo 1/˜λ je vlastním<br />
číslem matice A. Číslo 1<br />
˜λ = 1<br />
1<br />
10 − i<br />
30<br />
= 30 90 + 30i<br />
= = 9 + 3i<br />
3 − i 10<br />
leží v kruhu K 2 a může být vlastním číslem matice A. Číslo ˜λ = 1 10 − i tedy může být vlastním<br />
30<br />
číslem matice A −1 .<br />
20
3 Aplikace Geršgorinovy věty: odhad čísla podmíněnosti<br />
Příklad 3.1: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte zdola<br />
⎞<br />
a shora číslo podmíněnosti matice<br />
158 12 −1/2 5<br />
A (intervalový odhad), A = ⎜ 12 867 −1 24<br />
⎟<br />
⎝−1/2 −1 19 3/2⎠ . K výpočtu čísla podmíněnosti κ(A)<br />
5 24 3/2 371<br />
použijte spektrální normu ‖ · ‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná<br />
a symetrická.)<br />
Řešení: Z definice κ(A) = ‖A‖ 2 ‖A −1 ‖ 2 .<br />
Matice A je reálná a symetrická ⇒ vlastní čísla jsou reálná a ‖C‖ 2 = ̺(A).<br />
Podle Geršgorinovy věty leží všechna vlastní čísla matice C ve sjednocení kruhů, v našem<br />
případě úseček<br />
K 1 = {z ∈ R : |158 − z| ≤ 17,5},<br />
K 2 = {z ∈ R : |867 − z| ≤ 37},<br />
K 3 = {z ∈ R : |19 − z| ≤ 3},<br />
K 4 = {z ∈ R : |371 − z| ≤ 30,5}.<br />
Všechny úsečky leží v kladné části reálné osy, vlastní čísla tedy jsou kladná, proto ̺(A) = λ max ,<br />
kde λ max je největší vlastní číslo matice A. Tudíž (viz K 2 ) ‖A‖ 2 = λ max ∈ [830, 904].<br />
Všechna vlastní čísla matice A jsou kladná, tedy i všechna vlastní čísla matice A −1 jsou<br />
kladná, tudíž ‖A −1 ‖ 2 = ̺(A −1 ) = 1/λ min , kde λ min je nejmenší vlastní číslo matice A. Protože<br />
λ min ∈ [16,22], platí ‖A −1 ‖ 2 ∈ [1/22, 1/16].<br />
Dostaneme tedy κ(A) ∈ [830/22, 904/16] = [415/11, 113/2].<br />
Příklad 3.2: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte<br />
⎞<br />
zdola a shora číslo podmíněnosti matice C<br />
210 8 0 5<br />
(intervalový odhad), C = ⎜ 8 470 1 −14<br />
⎟<br />
⎝ 0 1 8 −1 ⎠ .<br />
5 −14 −1 980<br />
K výpočtu čísla podmíněnosti κ(C) použijte spektrální normu ‖·‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná<br />
a symetrická.)<br />
Řešení: κ(C) = ‖C‖ 2 ‖C −1 ‖ 2 .<br />
Matice C je reálná a symetrická ⇒ ‖C‖ 2 = max i=1,2,3,4 |λ i |, kde λ i jsou vlastní čísla matice<br />
C (všechna vlastní čísla matice C jsou reálná).<br />
Podle Geršgorinovy věty leží všechna vlastní čísla matice C ve sjednocení kruhů (přesněji<br />
úseček)<br />
K 1 = {z ∈ C : |210 − z| ≤ 13},<br />
K 2 = {z ∈ C : |470 − z| ≤ 23},<br />
K 3 = {z ∈ C : |8 − z| ≤ 2},<br />
K 4 = {z ∈ C : |980 − z| ≤ 20}.<br />
Vidíme, že vlastní čísla nemohou být nekladná, tudíž max i=1,2,3,4 |λ i | = λ 4 ∈ [960, 1000], ‖C‖ 2 ∈<br />
[960, 1000].<br />
21
Jest ‖C −1 ‖ 2 = 1/λ 3 , kde λ 3 je nejmenší vlastní číslo matice C. Protože λ 3 ∈ [6,10], platí<br />
‖C −1 ‖ 2 ∈ [1/10, 1/6].<br />
Dostaneme tedy κ(C) ∈ [96, 1000/6].<br />
Příklad 3.3: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte<br />
⎞<br />
zdola a shora číslo podmíněnosti matice<br />
252 −8 2 5<br />
A (intervalový odhad), A = ⎜−8 −900 −1 31<br />
⎟<br />
⎝ 2 −1 15 2 ⎠ . K výpočtu čísla podmíněnosti κ(A)<br />
5 31 2 348<br />
použijte spektrální normu ‖ · ‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná<br />
a symetrická.)<br />
Řešení: Z definice je κ(A) = ‖A‖ 2 ‖A −1 ‖ 2 . Matice A je reálná a symetrická, tedy vlastní čísla<br />
jsou reálná a ‖C‖ 2 = ̺(A).<br />
Podle Geršgorinovy věty leží všechna vlastní čísla matice C ve sjednocení kruhů, v našem<br />
případě úseček<br />
K 1 = {z ∈ R : |252 − z| ≤ 15} ⇒ [237, 267],<br />
K 2 = {z ∈ R : | − 900 − z| ≤ 40} ⇒ [−940, −860],<br />
K 3 = {z ∈ R : |15 − z| ≤ 5} ⇒ [10, 20],<br />
K 4 = {z ∈ R : |348 − z| ≤ 38} ⇒ [310, 386].<br />
Tři vlastní čísla tedy jsou kladná, jedno záporné, jeho absolutní hodnota je však větší než<br />
absolutní hodnota zbývajících vlastních čísel. Tudíž ‖A‖ 2 = ̺(A) ∈ [860, 940].<br />
Vlastní čísla matice A −1 jsou převrácenými hodnotami vlastních čísel matice A, proto leží<br />
v intervalech [1/267, 1/237], [−1/860, −1/940], [1/20, 1/10], [1/386, 1/310].<br />
Odtud ‖A −1 ‖ 2 = ̺(A −1 ) ∈ [1/20, 1/10].<br />
Dostaneme tedy κ(A) ∈ [860/20, 940/10] = [43, 94].<br />
Příklad 3.4: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte zdola<br />
⎞<br />
a shora číslo podmíněnosti matice<br />
−1050 −23 −2 25<br />
A (intervalový odhad), A = ⎜ −23 214 2 7<br />
⎟<br />
⎝ −2 2 −25 1 ⎠ . K výpočtu čísla podmíněnosti κ(A)<br />
25 7 1 470<br />
použijte spektrální normu ‖ · ‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná<br />
a symetrická.)<br />
Řešení: κ(A) ∈ [1000/30, 1100/20] = [100/3, 55]<br />
Příklad 3.5: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte<br />
⎞<br />
zdola a shora číslo podmíněnosti matice C<br />
−10 0 1 −1<br />
(intervalový odhad), C = ⎜ 0 207 7 5<br />
⎟<br />
⎝ 1 7 603 −14⎠ .<br />
−1 5 −14 800<br />
K výpočtu čísla podmíněnosti κ(C) použijte spektrální normu ‖·‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná a<br />
symetrická.)<br />
Řešení: κ(C) ∈ [780/12, 820/8] = [65, 205/2]<br />
22
Příklad 3.6: Pomocí Geršgorinovy<br />
⎛<br />
věty odhadněte zdola<br />
⎞<br />
a shora číslo podmíněnosti matice C<br />
320 1 8 21<br />
(intervalový odhad), kde C = ⎜ 1 9 1 −1<br />
⎟<br />
⎝ 8 1 −400 28 ⎠ .<br />
21 −1 28 −650<br />
K výpočtu čísla podmíněnosti κ(C) použijte spektrální normu ‖·‖ 2 . Svůj postup zdůvodněte.<br />
(Připomenutí: Je-li regulární matice reálná a symetrická, je matice k ní inverzní také reálná a<br />
symetrická.)<br />
Řešení: κ(C) ∈ [600/12, 700/6] = [50, 350/3]<br />
4 Normy vektorů a matic<br />
Příklad 4.1: Jsou dány matice A,B,C a vektory v,w = Av:<br />
⎛<br />
⎞<br />
3 −2 2 1<br />
( )<br />
A = ⎜−1 2 4 −3<br />
⎟ −2 3<br />
⎝ 5 1 1 4 ⎠ , B = , C =<br />
3 −2<br />
−3 4 −2 −1<br />
Vypočítejte ‖w‖ 1 , ‖w‖ 2 , ‖w‖ ∞ , ‖A‖ 1 , ‖A‖ ∞ , ‖B‖ 2 a ‖C‖ 2 .<br />
( ) 1 2<br />
, v =<br />
0 1<br />
⎛ ⎞<br />
1<br />
⎜−1<br />
⎟<br />
⎝−2⎠ .<br />
3<br />
Řešení: w = (4, −20,14, −6) T .<br />
‖w‖ 1 = 4 + 20 + 14 + 6 = 44.<br />
‖w‖ 2 = √ 16 + 400 + 196 + 36 = √ 648 = 2 √ 162 = 18 √ 2.<br />
‖w‖ ∞ = 20.<br />
‖A‖ 1 = max{12,9,9,9} = 12.<br />
‖A‖ ∞ = max{8,10,11,10} = 11.<br />
Matice B je reálná a symetrická. Její vlastní čísla jsou kořeny polynomu λ 2 + 4λ − 5, tj. λ 1 = 1,<br />
λ 2 = −5, tudíž ‖B‖ 2 = ̺(B) = 5.<br />
Matice C není symetrická. ‖C‖ 2 = √̺(C ( ) 1 2<br />
T C), kde C T C = . Charakteristický polynom<br />
2 5<br />
λ 2 − 6λ + 1 má kořeny λ 1 = 3 + 2 √ 2 a λ 2 = 3 − 2 √ 2.<br />
Odtud ‖C‖ 2 = √ 3 + 2 √ (<br />
2 = √ 1 + 2 √ √<br />
2 + 2 = (1 + √ 2) 2 = 1 + √ )<br />
2 .<br />
Poznámka: V modifikacích příkladu 4.1 mohou vystupovat i komplexní vektory a matice.<br />
Příklad 4.2: Jsou dány matice A,B a vektory v,w:<br />
⎛<br />
⎞<br />
⎛<br />
2 −1 3 −2<br />
( )<br />
A = ⎜ 1 2 4 3<br />
⎟ −1 2<br />
⎝−2 1 −3 1 ⎠ , B = , v = ⎜<br />
2 −1 ⎝<br />
5 2 2 −1<br />
2<br />
1<br />
−3<br />
−2<br />
⎞<br />
⎟<br />
⎠ ,<br />
w = Av.<br />
Vypočítejte ‖w‖ 2 , ‖A‖ 1 , ‖A‖ ∞ a ‖B‖ 2 .<br />
Řešení: ‖w‖ 2 = ‖(−2, −14,4,8) T ‖ 2 = √ 280 = 2 √ 70.<br />
‖A‖ 1 = max{10,6,12,7} = 12.<br />
‖A‖ ∞ = max{8,10,7,10} = 10.<br />
Matice B je symetrická. Její vlastní čísla jsou kořeny polynomu λ 2 +2λ −3, tj. λ 1 = 1, λ 2 = −3,<br />
tudíž ‖B‖ 2 = 3.<br />
23
Příklad 4.3: Jsou dány matice A,B,C a vektory v,w:<br />
⎛<br />
⎞<br />
2 −1 2 a<br />
( )<br />
A = ⎜−1 0 4 −4<br />
⎟ −1 3<br />
⎝ 5 −1 2 4 ⎠ , B = , C =<br />
3 −1<br />
−3 2 −4 −1<br />
( ) 1 −1<br />
, v =<br />
1 1<br />
⎛<br />
⎜<br />
⎝<br />
2<br />
3<br />
−1<br />
−2<br />
⎞<br />
⎟<br />
⎠ ,<br />
w = Av.<br />
Najděte takové záporné reálné číslo a, aby platilo ‖w‖ 2 = 7 √ 2. Tuto hodnotu a použijte i k<br />
výpočtu ‖w‖ 1 , ‖w‖ ∞ , ‖A‖ 1 , ‖A‖ ∞ . Dále stanovte ‖B‖ 2 a ‖C‖ 2 .<br />
Řešení: w = (−1 − 2a,2, −3,6) T a ‖w‖ 2 = √ 49 + (1 + 2a) 2 . Odtud a = −4.<br />
Pak w = (7,2, −3,6) T a ‖w‖ 1 = 7 + 2 + 3 + 6 = 18.<br />
‖w‖ ∞ = 7.<br />
‖A‖ 1 = max{11,4,12,13} = 13.<br />
‖A‖ ∞ = max{9,9,12,10} = 12.<br />
Matice B je symetrická. Její vlastní čísla jsou kořeny polynomu λ 2 +2λ −8, tj. λ 1 = 2, λ 2 = −4,<br />
tudíž ‖B‖ 2 = 4.<br />
Matice C není symetrická. ‖C‖ 2 = √̺(C ( ) 2 0<br />
T C), kde C T C = . Vlastní číslo 2 je dvojnásobné<br />
0 2<br />
a ‖C‖ 2 = √ 2.<br />
Příklad 4.4: Jsou dány matice A,B,C a vektory v,w:<br />
⎛<br />
⎞<br />
2 −1 2 −4<br />
( )<br />
A = ⎜−1 1 4 −4<br />
⎟ −2 3<br />
⎝ 2 −1 2 4 ⎠ , B = , C =<br />
3 −2<br />
a 0 −4 −1<br />
( ) −1 −1<br />
, v =<br />
1 1<br />
⎛ ⎞<br />
−2<br />
⎜ 3<br />
⎟<br />
⎝−2⎠ ,<br />
−1<br />
w = Av.<br />
Najděte takové záporné reálné číslo a, aby platilo ‖w‖ 2 = 10 √ 5. Tuto hodnotu a použijte i k<br />
výpočtu ‖w‖ 1 , ‖w‖ ∞ , ‖A‖ 1 , ‖A‖ ∞ . Dále stanovte ‖B‖ 2 a ‖C‖ 2 .<br />
Řešení: w = (−7,1, −15, −2a+9) T a ‖w‖ 2 = √ 275 + (2a − 9) 2 . Odtud (2a −9) 2 = 500 −275 =<br />
225, tedy a = −3.<br />
Pak w = (−7,1, −15,15) T a ‖w‖ 1 = 7 + 1 + 15 + 15 = 38.<br />
‖w‖ ∞ = 15.<br />
‖A‖ 1 = max{8,3,12,13} = 13.<br />
‖A‖ ∞ = max{9,10,9,8} = 10.<br />
Matice B je symetrická. Její vlastní čísla jsou kořeny polynomu λ 2 +4λ −5, tj. λ 1 = 1, λ 2 = −5,<br />
tudíž ‖B‖ 2 = 5.<br />
Matice C není symetrická. ‖C‖ 2 = √̺(C ( ) 2 2<br />
T C), kde C T C = . Charakteristický polynom<br />
2 2<br />
λ 2 − 4λ, vlastní čísla 0 a 4, tedy ‖C‖ 2 = √ 4 = 2.<br />
Příklad 4.5: Necht’ matice A a vektor z jsou:<br />
⎛ ⎞ ⎛ ⎞<br />
1 a 2 1<br />
A = ⎝−2 0 b⎠, z = ⎝−1⎠ .<br />
c 1 2 1<br />
Pomocí A a z jsou zadány vektory v a w, konkrétně v = Az a w = A T z. Nalezněte takové<br />
hodnoty a,b,c ∈ R, aby v = w a ‖v‖ 2 = 2 √ 2.<br />
24
Řešení:<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
1 a 2 1 3 − a<br />
v = Az = ⎝−2 0 b⎠<br />
⎝−1⎠ = ⎝−2 + b⎠ ,<br />
c 1 2 1 c + 1<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
1 −2 c 1 3 + c<br />
w = A T z = ⎝a 0 1⎠<br />
⎝−1⎠ = ⎝a + 1⎠.<br />
2 b 2 1 4 − b<br />
Z rovnosti v = w dostáváme<br />
a + c = 0,<br />
a − b = −3,<br />
b + c = 3<br />
s řešením a = −p, b = 3 − p a c = p, kde p je reálný parametr.<br />
Vyjádříme ‖v‖ 2 2 pomocí p<br />
‖v‖ 2 2 = ‖(3 + p,1 − p,p + 1)‖ 2 2 = (3 + p) 2 + (1 − p) 2 + (p + 1) 2<br />
což s podmínkou ‖v‖ 2 2 = 8 dává rovnici<br />
= 9 + 6p + p 2 + 1 − 2p + p 2 + p 2 + 2p + 1 = 3p 2 + 6p + 11,<br />
3p 2 + 6p + 11 = 8, upravenou na p 2 + 2p + 1 = 0<br />
s řešením p 1,2 = −1.<br />
Hledané parametry tedy jsou a = 1, b = 4 a c = −1.<br />
Dosazením těchto hodnot do matice A a vypočtením v = Az, w = A T z a ‖v‖ 2 se ověří, že<br />
v = w a ‖v‖ 2 = 2 √ 2.<br />
Příklad 4.6: Je dána matice A a vektor u:<br />
( a 2b<br />
A =<br />
1 c<br />
)<br />
, u =<br />
( 2<br />
−1)<br />
.<br />
Nalezněte takové hodnoty parametrů a,b,c ∈ R, aby platilo (zároveň!) Au = v = A T u, u je<br />
vlastní vektor matice A příslušný nějakému reálnému vlastnímu číslu a ‖v‖ 2 = √ 10.<br />
Řešení:<br />
v = Au =<br />
( )( ) a 2b 2<br />
=<br />
1 c −1<br />
Z rovnosti v = A T u dostáváme<br />
( ) ( )<br />
2a − 2b<br />
, A T a 1 2<br />
u =<br />
=<br />
2 − c<br />
2b c)(<br />
−1<br />
2a − 2b = 2a − 1 ⇒ b = 1 2 ,<br />
2 − c = 4b − c ⇒ b = 1 2 .<br />
Označme λ ∈ R příslušné vlastní číslo, tj. v = Au = λu. Pak dostaneme<br />
( ) 2a − 1<br />
.<br />
4b − c<br />
10 = ‖v‖ 2 2 = ‖Au‖2 2 = ‖λu‖2 2 = (2λ)2 + (−λ) 2 = 5λ 2 ⇒ λ = ± √ 2.<br />
25
Z Au = λu a b = 1/2 dále obdržíme<br />
Odtud<br />
Řešením tedy jsou dvě trojice hodnot a,b,c.<br />
2a − 2b = 2λ ⇒ a = 1 2 + λ,<br />
2 − c = −λ ⇒ c = 2 + λ.<br />
λ = √ 2 ⇒ a = 1 2 + √ 2, b = 1 2 , c = 2 + √ 2;<br />
λ = − √ 2 ⇒ a = 1 2 − √ 2, b = 1 2 , c = 2 − √ 2.<br />
Příklad 4.7: Jsou dány matice A,B,C a vektory v,w:<br />
⎛ ⎞<br />
⎛ ⎞<br />
3 −4 2 ( ) ( ) −1<br />
A = ⎝−5 a 1/2⎠ −1 3 1 1<br />
, B = , C = , v = ⎝ 3 ⎠, w = Av.<br />
3 −1 2 1<br />
−2 7 −6<br />
4<br />
Najděte takové celé číslo a, aby platilo ‖w‖ 2 = 5 √ 3. Tuto hodnotu a použijte i k výpočtu ‖w‖ 1 ,<br />
‖w‖ ∞ , ‖A‖ 1 , ‖A‖ ∞ . Dále stanovte ‖B‖ 2 a ‖C‖ 2 .<br />
Řešení: w = (−7,3a + 7, −1) T a 25 · 3 = ‖w‖ 2 2 = 49 + (3a + 7)2 + 1. Odtud (3a + 7) 2 = 25, tedy<br />
a = −4.<br />
Pak w = (−7, −5, −1) T a ‖w‖ 1 = 7 + 5 + 1 = 13.<br />
‖w‖ ∞ = 7.<br />
‖A‖ 1 = max{10,15,17/2} = 15.<br />
‖A‖ ∞ = max{9,19/2,15} = 15.<br />
Matice B je symetrická. Její vlastní čísla jsou kořeny polynomu λ 2 +2λ −8, tj. λ 1 = −4, λ 2 = 2,<br />
tudíž ‖B‖ 2 = 4.<br />
Matice C není symetrická. ‖C‖ 2 = √̺(C T C), kde C T C =<br />
λ 2 − 7λ + 1, vlastní čísla 7+3√ 5<br />
2<br />
a 7−3√ 5<br />
2<br />
, tedy ‖C‖ 2 =<br />
Příklad 4.8: Je dána matice A a vektor u:<br />
( ) a b<br />
A = , u =<br />
b 2a<br />
√<br />
7+3 √ 5<br />
2<br />
.<br />
( ) 1<br />
.<br />
−3<br />
( ) 5 3<br />
. Charakteristický polynom<br />
3 2<br />
Výpočtem nalezněte všechny takové dvojice hodnot parametrů a,b ∈ R a čísel λ ∈ R, aby<br />
zároveň platilo:<br />
(i) u je vlastní vektor matice A příslušný nějakému reálnému vlastnímu číslu λ;<br />
(ii) ‖Au‖ 2 = 2 √ 10.<br />
Proved’te zkoušku správnosti řešení.<br />
Řešení: Nejprve se zjistí, že λ = ±2. Pro λ = 2 dostaneme a = 16<br />
17 , b = − 6 . Pro λ = −2<br />
17<br />
dostaneme a = − 16<br />
17 , b = 6 17 .<br />
Zkouška<br />
1<br />
17<br />
( 16 −6<br />
−6 32)( 1<br />
−3<br />
)<br />
=<br />
( 2<br />
−6)<br />
,<br />
( )<br />
1 −16 6 1<br />
=<br />
17 6 −32)(<br />
−3<br />
( ) −2<br />
, ‖(2, −6)‖<br />
6<br />
2 = 2 √ 10.<br />
26
5 Gaussova eliminace<br />
Příklad 5.1: Gaussovou eliminační metodou vyřešte soustavu lineárních algebraických rovnic:<br />
−4U 1 + U 2 = 40,<br />
U 1 − 2U 2 + U 3 = 30,<br />
U 2 − 4U 3 = 24.<br />
Řešení:<br />
U 1 = − 53 3 , U 2 = − 92<br />
3 , U 3 = − 41 3 .<br />
(Doporučuji provést zkoušku správnosti řešení dosazením do výchozí soustavy rovnic.)<br />
Poznámka: Úlohy, jež reprezentuje příklad 5.1, nebývají zadávány samostatně, ale bývají<br />
součástí rozsáhlejších úkolů, viz kapitoly s příklady zaměřenými na metodu sítí.<br />
6 Iterační metody<br />
Příklad 6.1: Je dána soustava lineárních algebraických rovnic Cx = y, kde<br />
⎛ ⎞ ⎛ ⎞<br />
4 1 2 8<br />
C = ⎝1 2 0⎠ a y = ⎝2⎠ .<br />
1 1 3 6<br />
a) Soustavu řešte přibližně provedením dvou kroků Jacobiovy iterační metody s počátečním<br />
vektorem x (0) = (1, 1, 1) T , dostanete tedy přibližné řešení x (2) .<br />
b) Ukažte, že pro tuto soustavu Jacobiova metoda konverguje. (Stačí jedno zdůvodnění. V<br />
případě výpočtu normy použijte normu ‖ · ‖ ∞ .)<br />
c) Aniž byste vyřešením soustavy získali její přesné řešení ̂x, dvěma způsoby odhadněte<br />
velikost rozdílu ‖̂x − x (2) ‖ ∞ . Můžeme zaručit, že ‖̂x − x (2) ‖ ∞ < 0,4<br />
d) Můžeme zaručit, že ‖̂x − x (25) ‖ ∞ ≤ 0,01 Odpověd’ zdůvodněte.<br />
(Pomoc pro výpočty: log 10 2 ≈ 0,301, log 10 3 ≈ 0,477, log 10 5 ≈ 0,699, log 10 7 ≈ 0,845.)<br />
Řešení: a) Konstrukce matice pro iterační proces:<br />
Dále<br />
⎛1<br />
⎞⎛<br />
⎞ ⎛ ⎞<br />
A = D −1 4<br />
0 0 0 −1 −2 0 1/4 1/2<br />
Ĉ = ⎝ 1<br />
0<br />
2<br />
0⎠⎝−1 0 0 ⎠ = − ⎝1/2 0 0 ⎠.<br />
1<br />
0 0<br />
3<br />
−1 −1 0 1/3 1/3 0<br />
⎛ ⎞<br />
2<br />
b = D −1 y = ⎝1⎠ .<br />
2<br />
27
Během iteračního procesu x (k+1) = Ax (k) + b, kde k = 0,1,... , dostáváme<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 1/4 1/2 1 2 3/4 2 5/4<br />
x (1) = − ⎝1/2 0 0 ⎠ ⎝1⎠ + ⎝1⎠ = − ⎝1/2⎠ + ⎝1⎠ = ⎝1/2⎠ ,<br />
1/3 1/3 0 1 2 2/3 2 4/3<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 1/4 1/2 5/4 2 1/8 + 4/6 2<br />
x (2) = − ⎝1/2 0 0 ⎠ ⎝1/2⎠ + ⎝1⎠ = − ⎝ 5/8 ⎠ + ⎝1⎠<br />
1/3 1/3 0 4/3 2 5/12 + 1/6 2<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
19/24 2 29/24<br />
= − ⎝ 5/8 ⎠ + ⎝1⎠ = ⎝ 3/8 ⎠ .<br />
7/12 2 17/12<br />
b) Konvergence je zaručena nerovností ‖A‖ ∞ = 3 4<br />
< 1 (maximum řádkových součtů) nebo<br />
tím, že matice C má převládající diagonálu (viz odpovídající tvrzení v [4]).<br />
c) Použijme<br />
z [4], dostaneme první odhad<br />
Použijme<br />
‖̂x − x (2) ‖ ∞ ≤ ‖A‖ 2 ∞‖x 0 ‖ ∞ +<br />
‖̂x − x (k) ‖ ≤ ‖A‖ k ‖x 0 ‖ + ‖A‖k<br />
1 − ‖A‖ ‖b‖<br />
‖̂x − x (k) ‖ ≤<br />
( ) ‖A‖2 ∞ 3 2<br />
( 3 2<br />
‖b‖ ∞ = · 1 + 4)<br />
1 − ‖A‖ ∞ 4<br />
1<br />
· 2 = 81<br />
16 .<br />
4<br />
‖A‖<br />
1 − ‖A‖ ‖x(k) − x (k−1) ‖<br />
z [4], dostaneme druhý odhad<br />
‖̂x − x (2) ‖ ∞ ≤<br />
‖A‖ (<br />
∞<br />
‖x (2) − x (1) ‖ ∞ = 3<br />
−1<br />
1 − ‖A‖ ∞<br />
∥ 24 , −1<br />
8 , 1 )∥ ∥∥∥∞<br />
= 3 12 8 .<br />
Ano, z druhého odhadu dostáváme ‖̂x − x (2) ‖ ∞ ≤ 3/8 < 0,4.<br />
d) Analogicky k c) (první odhad) dostáváme<br />
( ) ( )<br />
‖̂x − x (25) ‖ ∞ ≤ ‖A‖ 25 ∞‖x 0 ‖ ∞ +<br />
‖A‖25 ∞ 3 25<br />
‖b‖ ∞ = 1 + 2 1 − ‖A‖ ∞ 4<br />
1<br />
4<br />
( ) 3 25<br />
= 9 .<br />
4<br />
Tážeme se, zda 2log 10 3 + 25log 10<br />
( 3<br />
4)<br />
je menší než −2 (tj. log10 0,01). Ukáže se, že ano (2 ·<br />
0.477 + 25(0.477 − 0.602) = 0.954 − 25 · 0.125 = −2.171 < −2).<br />
Můžeme tedy zaručit, že ‖̂x − x (25) ‖ ∞ ≤ 0,01.<br />
Poznámka: Při výpočtu vektorů x (1) a x (2) není nutné postupovat přímo dle předpisu x (k+1) =<br />
Ax (k) + b. Je například možné použít x (k+1) = D −1 (Ĉx(k) + y) nebo řešit soustavu Dx (k+1) =<br />
Ĉx (k) + y, viz také vztah pro výpočet x (k+1)<br />
i<br />
uvedený v [4].<br />
Příklad 6.2: Jako příklad 6.1, ale s použitím Gaussovy-Seidelovy metody. Poznamenejme, že<br />
při výpočtu Gaussových-Seidelových iterací není praktické přímo používat maticový zápis<br />
x (k+1) = (D − L) −1 Ux (k) + (D − L) −1 y, k = 0,1,... ,<br />
protože vyžaduje výpočet inverzní matice (D − L) −1 . Pohodlnější je použít vztah<br />
⎛<br />
⎞<br />
x (k+1)<br />
i<br />
= − 1 ∑i−1<br />
n∑<br />
⎝ c ij x (k+1)<br />
j<br />
+ c ij x (k) ⎠<br />
j<br />
+ y i<br />
, i = 1,2,... ,n,<br />
c ii c ii<br />
j=1<br />
j=i+1<br />
28
podrobnosti v [4].<br />
V odhadech chyby jsou možné i varianty s jinými normami vektorů a matic.<br />
Příklad 6.3: Je dána soustava lineárních algebraických rovnic Cx = y, kde<br />
⎛ ⎞ ⎛ ⎞<br />
5 1 1 5<br />
C = ⎝1 4 1⎠ a y = ⎝4⎠ .<br />
1 1 3 3<br />
a) Soustavu řešte přibližně provedením dvou kroků Jacobiovy iterační metody s počátečním<br />
vektorem x (0) = (1, 1, 1) T , dostanete tedy přibližné řešení x (2) .<br />
b) Ukažte, že pro tuto soustavu Jacobiova metoda konverguje. (Stačí jedno zdůvodnění. V<br />
případě výpočtu normy použijte normu ‖ · ‖ ∞ .)<br />
c) Aniž byste řešením soustavy získali její přesné řešení ̂x, odhadněte velikost rozdílu ‖̂x −<br />
x (2) ‖ ∞ .<br />
d) Můžeme zaručit, že ‖̂x − x (21) ‖ ∞ ≤ 0,001 Odpověd’ zdůvodněte.<br />
(Pomoc pro výpočet: log 10<br />
2<br />
3 ≈ −0,17609, log 10 4 ≈ 0,60206.)<br />
Řešení: a) Konstrukce matice pro iterační proces:<br />
⎛ ⎞⎛<br />
⎞ ⎛ ⎞<br />
1<br />
A = D −1 5<br />
0 0 0 −1 −1 0 1/5 1/5<br />
Ĉ = ⎝ 1<br />
0<br />
4<br />
0⎠⎝−1 0 −1⎠ = − ⎝1/4 0 1/4⎠.<br />
1<br />
0 0<br />
3<br />
−1 −1 0 1/3 1/3 0<br />
Dále<br />
⎛ ⎞<br />
1<br />
b = D −1 y = ⎝1⎠ .<br />
1<br />
Během iteračního procesu x (k+1) = Ax (k) + b, kde k = 0,1,... , dostáváme<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 1/5 1/5 1 1 2/5 1 3/5<br />
x (1) = − ⎝1/4 0 1/4⎠<br />
⎝1⎠ + ⎝1⎠ = − ⎝1/2⎠ + ⎝1⎠ = ⎝1/2⎠ ,<br />
1/3 1/3 0 1 1 2/3 1 1/3<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 1/5 1/5 3/5 1 1/10 + 1/15 1<br />
x (2) = − ⎝1/4 0 1/4⎠<br />
⎝1/2⎠ + ⎝1⎠ = − ⎝3/20 + 1/12⎠ + ⎝1⎠<br />
1/3 1/3 0 1/3 1 3/15 + 1/6 1<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
5/30 1 25/30<br />
= − ⎝14/60⎠ + ⎝1⎠ = ⎝23/30⎠ .<br />
11/30 1 19/30<br />
b) Konvergence je zaručena nerovností ‖A‖ ∞ = 2 3<br />
tím, že matice C má převládající diagonálu.<br />
c) Lze použít odhadu<br />
< 1 (maximum řádkových součtů) nebo<br />
‖̂x − x (2) ‖ ∞ ≤ ‖A‖ 2 ∞ ‖x 0‖ ∞ +<br />
( ) ‖A‖2 ∞ 2 2<br />
( 2 2<br />
‖b‖ ∞ = · 1 + 3)<br />
1 − ‖A‖ ∞ 3<br />
1<br />
· 1 = 16 9<br />
3<br />
nebo odhadu<br />
‖̂x − x (2) ‖ ∞ ≤<br />
‖A‖ (<br />
∞<br />
‖x (2) − x (1) ‖ ∞ = 2<br />
7<br />
1 − ‖A‖ ∞<br />
∥ 30 , 8<br />
30 , 9 )∥ ∥∥∥∞<br />
= 9 30 15 .<br />
29
d) Platí odhad<br />
‖̂x − x (21) ‖ ∞ ≤ ‖A‖ 21 ∞‖x 0 ‖ ∞ +<br />
( ) ‖A‖21 ∞ 2 21<br />
( 2 21 ( )<br />
‖b‖ ∞ = · 1 + 3)<br />
2<br />
21<br />
1 − ‖A‖ ∞ 3<br />
1<br />
· 1 = 4 .<br />
3<br />
3<br />
Tážeme se, zda log 10 4+21log 10<br />
( 2<br />
3)<br />
je menší než −3 (tj. log10 0,001). Ukáže se, že ano (−3.09583 <<br />
−3).<br />
Můžeme tedy zaručit, že ‖̂x − x (21) ‖ ∞ ≤ 0,001.<br />
Příklad 6.4: Je dána soustava lineárních algebraických rovnic Cx = y, kde<br />
⎛ ⎞ ⎛ ⎞<br />
4 1 0<br />
−4<br />
C = ⎝1 4 1⎠ a y = ⎝ 8 ⎠.<br />
0 1 4<br />
4<br />
a) Soustavu řešte přibližně provedením tří kroků Jacobiovy iterační metody s počátečním<br />
vektorem x (0) = (0, 1, 0) T , dostanete tedy přibližné řešení x (3) .<br />
b) Ukažte, že pro tuto soustavu Jacobiova metoda konverguje. (Stačí jedno zdůvodnění. V<br />
případě výpočtu normy použijte normu ‖ · ‖ ∞ .)<br />
c) Aniž byste řešením soustavy získali její přesné řešení ̂x, dvěma různými způsoby odhadněte<br />
velikost rozdílu ‖̂x − x (3) ‖ ∞ . Lze zaručit, že ‖̂x − x (3) ‖ ∞ ≤ 1/4<br />
Řešení: a) Konstrukce matice pro iterační proces:<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
1<br />
A = D −1 4<br />
0 0 0 −1 0<br />
Ĉ = ⎝ 1<br />
0<br />
4<br />
0⎠<br />
⎝−1 0 −1⎠ = − 1 0 1 0<br />
⎝1 0 1⎠ .<br />
1<br />
4<br />
0 0<br />
4<br />
0 −1 0 0 1 0<br />
Dále<br />
⎛ ⎞<br />
−1<br />
b = D −1 y = ⎝ 2 ⎠ .<br />
1<br />
Během iteračního procesu x (k+1) = Ax (k) + b, kde k = 0,1,... , dostáváme<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
0 −1 −1/4 −1 −5/4<br />
x (1) = A⎝1⎠ + ⎝ 2 ⎠ = − ⎝ 0 ⎠ + ⎝ 2 ⎠ = ⎝ 2 ⎠,<br />
0 1 −1/4 1 3/4<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
−5/4 −1 −1/2 −1 −3/2<br />
x (2) = A⎝<br />
2 ⎠ + ⎝ 2 ⎠ = ⎝ 1/8 ⎠ + ⎝ 2 ⎠ = ⎝17/8⎠ .<br />
3/4 1 −1/2 1 1/2<br />
⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞<br />
−3/2 −1 −17/32 −1 −49/32<br />
x (3) = A⎝17/8⎠ + ⎝ 2 ⎠ = ⎝ 1/4 ⎠ + ⎝ 2 ⎠ = ⎝ 9/4 ⎠ .<br />
1/2 1 −17/32 1 15/32<br />
b) Konvergence je zaručena nerovností ‖A‖ ∞ = 1 2<br />
< 1 (maximum řádkových součtů) nebo<br />
tím, že matice C má převládající diagonálu.<br />
c) Použije se odhad<br />
( )<br />
‖̂x − x (3) ‖ ∞ ≤ ‖A‖ 3 ∞ ‖x(0) ‖ ∞ +<br />
‖A‖3 ∞ 1 3<br />
( 1 3<br />
‖b‖ ∞ = · 1 + 2)<br />
2 = 5 1 − ‖A‖ ∞ 2<br />
8<br />
a odhad<br />
‖̂x − x (3) ‖ ∞ ≤<br />
‖A‖ (<br />
∞<br />
‖x (3) − x (2) ‖ ∞ = 1<br />
−49<br />
1 − ‖A‖ ∞<br />
∥ 32 + 3 2 , 9 4 − 17<br />
8 , 15<br />
32 − 1 )∥ ∥∥∥∞<br />
= 1 2 8 .<br />
30<br />
1<br />
2
Na základě druhého odhadu lze říci, že ‖̂x − x (3) ‖ ∞ ≤ 1/4.<br />
Příklad 6.5: Je dána soustava lineárních algebraických rovnic Cx = y, kde<br />
⎛ ⎞ ⎛ ⎞<br />
1 1<br />
−2<br />
2 2<br />
−2<br />
C = ⎝ 1 −3 1⎠ a y = ⎝−3⎠ .<br />
2 0 3<br />
0<br />
a) Soustavu řešte přibližně provedením dvou kroků Jacobiovy iterační metody s počátečním<br />
vektorem x (0) = (−1, 1, 1) T , dostanete tedy přibližné řešení x (2) .<br />
b) Ukažte, že pro tuto soustavu Jacobiova metoda konverguje. (Stačí jedno zdůvodnění. V<br />
případě výpočtu normy použijte normu ‖ · ‖ ∞ .)<br />
c) Aniž byste vyřešením soustavy získali její přesné řešení ̂x, odhadněte velikost rozdílu<br />
‖̂x − x (2) ‖ ∞ . Můžete zaručit, že ‖̂x − x (2) ‖ ∞ < 2<br />
d) Můžete zaručit, že ‖̂x − x (22) ‖ ∞ ≤ 0,001 Odpověd’ zdůvodněte.<br />
(Pomoc pro výpočty: log 10 2 ≈ 0,301, log 10 3 ≈ 0,477.)<br />
Řešení: a) Konstrukce matice pro iterační proces:<br />
⎛<br />
− 1 ⎞ ⎛<br />
A = D −1 2<br />
0 0 0 − 1<br />
Ĉ = ⎝ 0 − 1 2<br />
− 1 ⎞ ⎛<br />
⎞<br />
2<br />
0 1/4 1/4<br />
3<br />
0⎠<br />
⎝−1 0 −1⎠ = ⎝ 1/3 0 1/3⎠.<br />
1<br />
0 0<br />
3<br />
−2 0 0 −2/3 0 0<br />
Dále<br />
⎛ ⎞<br />
1<br />
b = D −1 y = ⎝1⎠ .<br />
0<br />
Během iteračního procesu x (k+1) = Ax (k) + b, kde k = 0,1,... , dostáváme<br />
⎛ ⎞ ⎛ ⎞<br />
3/2 17/12<br />
x (1) = ⎝ 1 ⎠ , x (2) = ⎝31/18⎠.<br />
2/3<br />
−1<br />
b) Konvergence je zaručena nerovností ‖A‖ ∞ = 2 3<br />
< 1 (maximum řádkových součtů) nebo<br />
tím, že matice C má převládající diagonálu.<br />
c) Z<br />
‖̂x − x (k) ‖ ≤<br />
‖A‖<br />
1 − ‖A‖ ‖x(k) − x (k−1) ‖<br />
dostaneme odhad<br />
‖̂x − x (2) ‖ ∞ ≤<br />
‖A‖ ∞<br />
1 − ‖A‖ ∞<br />
‖x (2) − x (1) ‖ ∞ = 10 3 .<br />
Z<br />
dostaneme odhad<br />
‖̂x − x (k) ‖ ≤ ‖A‖ k (‖x (0) ‖ +<br />
‖̂x − x (2) ‖ ∞ ≤ ‖A‖ 2 ∞<br />
)<br />
1<br />
1 − ‖A‖ ‖b‖<br />
(<br />
)<br />
‖x (0) 1<br />
‖ ∞ + ‖b‖ ∞ = 16 1 − ‖A‖ ∞ 9 .<br />
Ano, z druhého odhadu dostáváme ‖̂x − x (2) ‖ ∞ ≤ 16<br />
9 < 2.<br />
31
d) Analogicky k c) (druhý odhad) dostáváme<br />
(<br />
‖̂x − x (22) ‖ ∞ ≤ ‖A‖ 22 ∞ ‖x (0) ‖ ∞ +<br />
‖b‖ )<br />
∞<br />
=<br />
1 − ‖A‖ ∞<br />
( 2<br />
3) 22<br />
(<br />
1 + 1 1<br />
3<br />
)<br />
( ) 2 22<br />
= 4 .<br />
3<br />
Tážeme se, zda log 10 4 + 22log 10<br />
( 2<br />
3)<br />
je menší než −3 (tj. log10 0,001). Ukáže se, že ano (0,602 +<br />
22(0,301 − 0,477) = 0,602 − 22 · 0,176 = 0,602 − 3,872 < −3).<br />
Můžeme tedy zaručit, že ‖̂x − x (22) ‖ ∞ ≤ 0,001.<br />
7 Lineární zobrazení<br />
Příklad 7.1: Necht’ vektorový prostor V je dán takto:<br />
V = {v ∈ C 1 ([0,1]) : v(0) = 0}.<br />
Rozhodněte, zda zobrazení F 1 , F 2 , F 3 a F 4 daná předpisem<br />
jsou na V lineární zobrazení.<br />
F 1 (v) =<br />
∫ 1<br />
0<br />
F 2 (v) = v 3 (0) +<br />
F 3 (v) =<br />
∫ 1<br />
0<br />
F 4 (v) = |v|<br />
(2 + sinx)v(x)dx,<br />
∫ 1<br />
0<br />
v 2 (x)dx,<br />
e 2 (x)v ′ (x)dx,<br />
Řešení: Připomeňme, že zobrazení F z vektorového prostoru ˆV do vektorového prostoru W<br />
je lineární, jestliže pro každé celé číslo n a každá reálná čísla c 1 ,c 2 ,... ,c n a každé prvky<br />
v 1 ,v 2 ,...,v n ∈ ˆV platí<br />
Je zřejmé, že jestliže platí<br />
F(c 1 v 1 + c 2 v 2 + · · · + c n v n ) = c 1 F(v 1 ) + c 2 F(v 2 ) + · · · + c n F(v n ). (1)<br />
F(a 1 w 1 + a 2 w 2 ) = a 1 F(w 1 ) + a 2 F(w 2 ) (2)<br />
pro každé a 1 ,a 2 ∈ R a každé w 1 ,w 2 ∈ ˆV , platí i (1). Stačí tedy ověřit (2).<br />
Konkrétně: Zobrazení F 1 je lineární, nebot’<br />
F 1 (a 1 w 1 + a 2 w 2 ) =<br />
∫ 1<br />
0<br />
(2 + sin x)(a 1 w 1 (x) + a 2 w 2 (x))dx<br />
∫ 1<br />
∫ 1<br />
= a 1 (2 + sin x)w 1 (x)dx + a 2 (2 + sin x)w 2 (x)dx<br />
0<br />
= a 1 F(w 1 ) + a 2 F(w 2 ).<br />
Zobrazení F 2 je lineární, důkaz je obdobný jako u zobrazení F 1 , navíc se využije toho, že<br />
v ∈ V ⇒ v(0) = 0.<br />
Zobrazení F 3 není lineární, nebot’<br />
F 3 (a 1 w 1 + a 2 w 2 ) =<br />
=<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
(a 1 w 1 (x) + a 2 w 2 (x)) 2 dx<br />
(a 2 1w 2 1(x) + 2a 1 a 2 w 1 (x)w 2 (x) + a 2 2w 2 2(x))dx<br />
∫ 1<br />
= a 2 1F 3 (w 1 ) + a 2 2F 3 (w 2 ) + 2a 1 a 2 w 1 (x)w 2 (x)dx.<br />
32<br />
0<br />
0
Jistě se tedy dají najít funkce w 1 ,w 2 ∈ V a konstanty a 1 ,a 2 takové, že<br />
F 3 (a 1 w 1 + a 2 w 2 ) ≠ a 1 F 3 (w 1 ) + a 2 F 3 (w 2 ).<br />
Ještě jednodušší důkaz toho, že F 3 není lineární, je založen na tom, že v (2) může být a 2 = 0.<br />
Pak ovšem<br />
F 3 (a 1 w 1 ) = a 2 1 F 3(w 1 ),<br />
což (kromě speciálních případů a 1 ,w 1 ) odporuje (2).<br />
Zobrazení F 4 není lineární. V (2) stačí položit a 1 = −1 a a 2 = 0. Pak<br />
F 4 (−w 1 ) = | − w 1 | = |w 1 | ≠ −|w 1 | = −F 4 (w 1 ),<br />
pokud w 1 je nenulová funkce. (Udělejte si náčrtek například pro w 1 (x) = x.)<br />
Poznámka: Ověření rovnosti (2) lze rozložit do dvou kroků, totiž<br />
∀a ∈ R ∀w ∈ ˆV F(aw) = aF(w), (3)<br />
∀w 1 ,w 2 ∈ ˆV F(w 1 + w 2 ) = F(w 1 ) + F(w 2 ). (4)<br />
Poznámka: Příklady typu příkladu číslo 1 se nemusejí týkat jen zobrazení, jehož argumentem<br />
je prvek z prostoru funkcí. Prostor V může být vektorovým prostorem i jiných matematických<br />
objektů, např. uspořádaných n-tic či matic.<br />
Příklad 7.2: Rozhodněte, zda zobrazení f i : R 3 → R 2 , i = 1,2,3, je či není lineární:<br />
1) f 1 : (x,y,z) ↦→ (x + y, −x + 2z)<br />
2) f 2 : (x,y,z) ↦→ (x,0)<br />
3) f 3 : (x,y,z) ↦→ (5,z)<br />
Řešení: Lze vyjít z (2) nebo z (3)-(4). Pro ukázku zvolme druhou možnost.<br />
1) Násobení skalárem.<br />
∀a ∈ R ∀w = (x,y,z) ∈ R 3<br />
aw = (ax,ay,az) ↦→ (ax + ay, −ax + 2az) = a(x + y, −x + 2z,3z),<br />
tedy f 1 (aw) = af 1 (w).<br />
(Obraz výchozího vektoru je konstruován tak, že v první složce obrazu je součet první a<br />
druhé složky vzoru, druhá složka obrazu vznikne tím, že od dvojnásobku třetí složky vzoru<br />
odečteme hodnotu první složky vzoru.)<br />
Součet.<br />
∀w 1 = (x 1 ,y 1 ,z 1 ),w 2 = (x 2 ,y 2 ,z 2 ) ∈ R 3<br />
(w 1 + w 2 ) = (x 1 + x 2 ,y 1 + y 2 ,z 1 + z 2 ) ↦→ (x 1 + x 2 + y 1 + y 2 , −x 1 − x 2 + 2z 1 + 2z 2 ) = (x 1 +<br />
y 1 , −x 1 + 2z 1 ) + (x 2 + y 2 , −x 2 + 2z 2 ),<br />
tedy f(w 1 + w 2 ) = f 1 (w 1 ) + f 1 (w 2 ).<br />
Zobrazení je lineární.<br />
2) Stejným postupem se zjistí, že zobrazení je lineární, zkráceně<br />
(ax,ay,az) ↦→ (ax,0) = a(x,0) a (x 1 + x 2 ,y 1 + y 2 ,z 1 + z 2 ) ↦→ (x 1 + x 2 ,0) = (x 1 ,0) + (x 2 ,0).<br />
3) Pozorujeme, že (ax,ay,az) ↦→ (5,az) ≠ a(5,z) = af 3 (x,y,z). Zobrazení není lineární.<br />
Příklad 7.3: Rozhodněte, zda zobrazení f i : R 3 → R 3 , i = 1,2,3, je či není lineární.<br />
1) f 1 (x,y,z) = (x + y + z,2x + y,3z)<br />
2) f 2 (x,y,z) = (y,y,y)<br />
3) f 3 (x,y,z) = (z,xy,0)<br />
4) f 4 (x,y,z) = (y,x + y,1)<br />
33
Řešení: Označme α ≡ (x 1 ,y 1 ,z 1 ) a β ≡ (x 2 ,y 2 ,z 2 ). Pak pro a,b ∈ R, α,β ∈ R 3 jest<br />
f i (aα + bβ) = af i (α) + bf i (β),<br />
jestliže i = 1,2, tj. f 1 a f 2 jsou lineární zobrazení, f 3 a f 4 nejsou lineární zobrazení.<br />
Příklad 7.4: Je dán vektorový prostor<br />
V = {v ∈ C 1 ([−1,1]) : v(1) = 0}.<br />
Rozhodně, zda zobrazení f i : V → R, i = 1,2,3,4,5, je či není lineární:<br />
f 1 (v) = v(0),<br />
f 2 (v) = v 2 (1),<br />
f 3 (v) = ∫ 1<br />
−1 v(x)sin(x)dx,<br />
f 4 (v) = ∫ 1/2<br />
0<br />
v(x)dx,<br />
f 5 (v) = ∫ −1/2<br />
−1<br />
v(x)ln |x|dx + ∫ 1<br />
−1/2<br />
(v(x) − v(x)cos(x))dx.<br />
Nezapomeňte zdůvodnit své závěry.<br />
Řešení: Pro ∀c ∈ R a ∀v,w ∈ V :<br />
f 1 (cv) = cv(0) = cf 1 (v), f 1 (v + w) = v(0) + w(0) = f 1 (v) + f 1 (w), lineární zobrazení (LZ);<br />
f 2 (cv) = 0 = cf 2 (v), f 2 (v + w) = 0 = f 2 (v) + f 2 (w), LZ;<br />
f 3 (cv) = c ∫ 1<br />
−1 v(x)sin(x)dx = cf 3(v), f 3 (v + w) = ∫ 1<br />
−1 v(x)sin(x)dx + ∫ 1<br />
−1 w(x)sin(x)dx =<br />
f 3 (v) + f 3 (w), LZ;<br />
f 4 LZ (postup jako u f 3 );<br />
f 5 (v), LZ (postup jako u f 3 ).<br />
Pozor, abychom dokázali linearitu zobrazení, musíme dokázat jeho linearitu jak vzhledem<br />
k násobení, tak ke sčítání. Při důkazu toho, že zobrazení není lineární, postačí ukázat, že nemá<br />
vlastnost linearity vzhledem k násobení nebo vhledem ke sčítání.<br />
Příklad 7.5: Zobrazení F je (postupně čtyřmi způsoby) definováno na prostoru C 1 ([a,b]) funkcí<br />
jednou spojitě diferencovatelných na uzavřeném intervalu [a,b]. Tyto funkce zobrazuje do prostoru<br />
funkcí spojitých na [a,b]. Rozhodněte, zda zobrazení F je lineární, je-li F(u) = α, kde<br />
u ∈ C 1 ([a,b]) a<br />
a) α(x) = (sin xu(x)) ′ + ∫ x<br />
a u(t)et dt v každém bodě x ∈ [a,b];<br />
b) α(x) = max{e x ,u(x)} v každém bodě x ∈ [a,b];<br />
c) α(x) = max{0,u(x)} + min{0,u(x)} v každém bodě x ∈ [a,b];<br />
d) α(x) = 5u(x) − 3 2 u ( )<br />
a+b<br />
2<br />
v každém bodě x ∈ [a,b].<br />
Své rozhodnutí zdůvodněte.<br />
Řešení: a) Necht’ c ∈ R, u ∈ C 1 ([a,b]) a α = F(u). Pak F(cu) = ρ, kde<br />
ρ(x) = (sin x(cu(x))) ′ +<br />
= cα(x), x ∈ [a,b].<br />
∫ x<br />
a<br />
cu(t)e t dt = c(sin xu(x)) ′ + c<br />
Necht’ navíc v ∈ C 1 ([a,b]) a β = F(v). Pak F(u + v) = ξ, kde<br />
Zobrazení F tedy je lineární.<br />
ξ(x) = (sin x(u(x) + v(x))) ′ +<br />
= α(x) + β(x), x ∈ [a,b].<br />
∫ x<br />
a<br />
∫ x<br />
a<br />
(u(t) + v(t))e t dt<br />
u(t)e t dt<br />
34
) Necht’ 0 ≠ c ∈ R a u(x) = 0 pro každé x ∈ [a,b]; funkce u ∈ C 1 ([a,b]). Zřejmě F(u) =<br />
e x = F(cu) ≠ cF(u). Zobrazení F tedy není lineární.<br />
c) Z definice vidíme, že pro každou funkci u ∈ C 1 ([a,b]) a pro každý bod x ∈ [a,b] platí<br />
u(x) ≥ 0 ⇒ α(x) = u(x),<br />
u(x) < 0 ⇒ α(x) = u(x).<br />
Je tedy F(u) = u (identita), zobrazení F tudíž je lineární.<br />
d) Necht’ c ∈ R, u,v ∈ C 1 ([a,b]), α = F(u) a β = F(v). Pak F(cu) = ρ a F(u + v) = ξ, kde<br />
( ) a + b<br />
ρ(x) = 5(cu(x)) − 3 2 cu = cα(x), x ∈ [a,b];<br />
2<br />
( ) ( ))<br />
a + b a + b<br />
ξ(x) = 5(u(x) + v(x)) − 3<br />
(u<br />
2 + v<br />
2 2<br />
Zobrazení F tedy je lineární.<br />
= α(x) + β(x), x ∈ [a,b].<br />
Příklad 7.6: Rozhodněte, zda zobrazení f i : R 3 → R 3 , i = 1,2,3,4,5, je či není lineární na<br />
vektorovém podprostoru V = {(x,y,z) ∈ R 3 : y = 2x} s vazbou mezi složkami x a y.<br />
1) f 1 (v) = (x − y,x + 3y − 5z,y/2), kde v ≡ (x,y,z) ∈ V ;<br />
2) f 2 (v) = (−y, −x,2y 2 − 8x 2 ), kde v ≡ (x,y,z) ∈ V ;<br />
3) f 3 (v) = (0,z,0), kde v ≡ (x,y,z) ∈ V ;<br />
4) f 4 (v) = (−y,0,1), kde v ≡ (x,y,z) ∈ V ;<br />
5) f 5 (v) = (0,0,0), kde v ≡ (x,y,z) ∈ V .<br />
Platí pro některé (některá) z uvedených zobrazení, že je (jsou) lineární na prostoru V , ale nejsou<br />
lineární na prostoru R 3 (tj. pro v ≡ (x,y,z) ∈ R 3 )<br />
Své odpovědi zdůvodněte.<br />
Řešení: Jestliže zobrazení bude lineární na prostoru R 3 , pak bude lineární i na podprostoru V<br />
(proč). Zeved’me označení v ≡ (x,y,z) a u ≡ (r,s,t).<br />
1) Pro v,u ∈ R 3 a a ∈ R je f 1 (av) = a(x − y,x + 3y − 5z,y/2) a také f 1 (u + v) =<br />
(x − y,x + 3y − 5z,y/2) + (r − s,r + 3s − 5t,s/2). Zobrazení je tedy lineární na R 3 i V .<br />
2) Pro v ∈ R 3 a a ∈ R je<br />
f 2 (av) = (−ay, −ax,2(ay) 2 − 8(ax) 2 ) = a(−y, −x,2ay 2 − 8ax 2 ) ≠ af 2 (v),<br />
pokud a ≠ 0 a a ≠ 1. Zobrazení tedy není lineární na R 3 .<br />
Jestliže však v ∈ V , pak<br />
f 2 (v) = (−y, −x,2y 2 − 8x 2 ) = (−y, −x,2(2x) 2 − 8x 2 ) = (−y, −x,0),<br />
využili jsme definice vazby mezi x a y.<br />
Pro u,v ∈ V a a ∈ R jsou w = av i s = u + v prvky podprostoru V , tj. w = (w 1 ,w 2 ,w 3 ),<br />
kde w 2 = 2w 1 , a s = (s 1 ,s 2 ,s 3 ), kde s 2 = 2s 1 .<br />
Potom f 2 (w) = (−w 2 , −w 1 ,0) = (−ay, −ax,0) = af 2 (v) a f 2 (s) = (−s 2 , −s 1 ,0) = (−s −<br />
y, −r − x,0) = f 2 (u) + f 2 (v). Zobrazení f 2 je lineární na podprostoru V .<br />
3) Snadno se ukáže, že zobrazení je lineární na R 3 i na V .<br />
4) Pro a ∈ R je f 4 (av) = (−ay,0,1) ≠ a(−y,0,1), pokud a ≠ 1. Zobrazení není lineární na<br />
R 3 ani na V .<br />
5) Snadno se ukáže, že zobrazení je lineární na R 3 ani na V .<br />
35
8 Okrajové úlohy v 1D: řešitelnost<br />
Příklad 8.1: Je dána okrajová úloha<br />
Kolik má řešení<br />
Řešení: Jelikož −π není vlastní číslo úlohy<br />
u ′′ − πu = ln(π + x),<br />
u(0) = 0, u(π) = 0.<br />
u ′′ + λu = 0,<br />
u(0) = 0, u(π) = 0,<br />
má daná úloha právě jedno řešení.<br />
(Studenti mohou mít příslušný systém vlastních čísel na povoleném taháku, takže vidí, že −π<br />
není vlastní číslo úlohy. Stačí ovšem i jednodušší zdůvodnění tím, že vlastní čísla výše uvedené<br />
homogenní úlohy jsou kladná.)<br />
Příklad 8.2: Zjistěte, jak závisí počet řešení na parametru λ ∈ R:<br />
u ′′ + λu = sin(−x) + 5sin 3x − 8sin 7x + 1 2 sin22x,<br />
u(0) = u(π) = 0.<br />
Řešení: Vlastní čísla jsou 5 V ≡ {k 2 : k = 1,2,3,... }, vlastní funkce příslušná k λ = k 2 je<br />
u k = sin kx. Pravá strana f ≡ −u 1 + 5u 3 − 8u 7 + 1 2 u 22.<br />
1. Jestliže λ /∈ V , pak právě jedno řešení.<br />
2. Pro k = 1,3,7,22 je (u k ,f) ≠ 0, tedy pro λ = 1,9,49,22 2 úloha nemá řešení (22 2 = 484).<br />
3. Jestliže λ ∈ V \ {1,9,49,22 2 }, pak úloha má nekonečně mnoho řešení.<br />
Příklad 8.3: Zjistěte, jak závisí počet řešení okrajové úlohy<br />
u ′′ + λu = 3sin 4x − sin5x + 8sin 9x, u(0) = 0 = u(π),<br />
na parametru λ ∈ R. Odpověd’ jasně zformulujte vzhledem k hodnotám parametru λ.<br />
Řešení: Vlastní čísla λ = k 2 , kde k = 1,2,3,... Příslušné vlastní fukce u k = sinkx. Pravá strana<br />
f = 3u 4 − u 5 + 8u 9 .<br />
λ ∈ R \ {k 2 : k = 1,2,... } (λ není vlastní číslo) ⇒ právě jedno řešení.<br />
λ = 16 (k = 4) ⇒ nemá řešení (nebot’ pravá strana f není ortogonální k u 4 (proč)).<br />
λ = 25 (k = 5) ⇒ nemá řešení (nebot’ pravá strana f není ortogonální k u 5 (proč)).<br />
λ = 81 (k = 9) ⇒ nemá řešení (nebot’ pravá strana f není ortogonální k u 9 (proč)).<br />
λ ∈ M, kde M = {k 2 : k ∈ N \ {4,5,9}} ⇒ má nekonečně mnoho řešení (pravá strana f je<br />
ortogonální k u k , pokud k ≠ 4, k ≠ 5, k ≠ 9.<br />
Hodnocení by mělo být nižší, pokud odpověd’ není formulovaná pro λ, ale jen pro k.<br />
Příklad 8.4: Zjistěte, jak závisí počet řešení na parametru λ ∈ R:<br />
u ′′ + λu = sin(−2x) + 3sin(−6x) − 2sin 10x + π sin 18x,<br />
u(0) = u(π/2) = 0.<br />
5 Obecně k 2 π2<br />
(b−a) 2 , vlastní funkce u k (x) = sin kπ(x−a)<br />
b−a<br />
, kde k = 1, 2, . . .<br />
36
(Nezapomeňte své závěry řádně zdůvodnit.)<br />
Řešení: Vlastní čísla jsou V ≡ {4k 2 : k = 1,2,3,... }, vlastní funkce příslušná k λ = 4k 2 je<br />
u k = sin 2kx. Pravá strana f ≡ −u 1 − 3u 3 − 2u 5 + πu 9 .<br />
1. Jestliže λ /∈ V , pak právě jedno řešení.<br />
2. Pro k = 1,3,5,9 je (u k ,f) ≠ 0, tedy pro λ = 4,36,100,324 úloha nemá řešení.<br />
3. Jestliže λ ∈ V \ {4,36,100,324}, pak úloha má nekonečně mnoho řešení.<br />
Příklad 8.5: Je dána okrajová úloha<br />
u ′′ + u = f,<br />
u(−π/2) = 0 = u(π/2).<br />
Rozhodněte, zda a kolik má řešení, jestliže a) f ≡ x 2 ; b) f ≡ x 3 .<br />
Své rozhodnutí řádně zdůvodněte (výpočtem, úvahou).<br />
Doporučení: Inspiraci hledejte mj. v náčrtcích a v říkance: V Monte Carlu sudá, lichá<br />
žoky peněz přináší,<br />
v em á čtyřce<br />
při písemce<br />
těžkou práci zaplaší.<br />
Řešení: Pro tuto úlohu jsou vlastní čísla dána hodnotami k 2 π2 , kde k = 1,2,3,... Hodnota 1<br />
(b−a) 2 tedy je vlastním číslem s příslušnou vlastní funkcí u 1 (x) = sin kπ(x−a)<br />
b−a<br />
∣ = sin ( x + π<br />
k=1<br />
2)<br />
= cos x.<br />
Ta je na intervalu [ − π 2 , π (<br />
2]<br />
sudá a na intervalu −<br />
π<br />
2 , π 2)<br />
kladná.<br />
a) Platí (u 1 ,f) ≠ 0, nebot’ u 1 (x)x 2 je funkce kladná na ( − π 2 ,0) ∪ ( 0, π 2)<br />
. Úloha nemá řešení.<br />
b) Platí (u 1 ,f) = 0 nebot’ u 1 (x)x 3 je funkce lichá na ( − π 2 , π 2)<br />
. Úloha má nekonečně mnoho<br />
řešení.<br />
Pokud to někdo bude počítat integrací, je to OK, i když pracné. Strhávejte však body, pokud<br />
integrace bude chybně provedena.<br />
Příklad 8.6: Zjistěte, jak závisí počet řešení na parametru λ ∈ R v úloze<br />
u ′′ + λu = 2sin x + sin(−3x) + 3sin(−5x) − 1 3 sin7x + 1 sin 3x,<br />
2<br />
u(0) = u ′ (π/2) = 0.<br />
Řešení: Vlastní čísla jsou 6 V ≡ {(2k + 1) 2 : k = 0,1,2,... }, vlastní funkce příslušná k λ =<br />
(2k + 1) 2 je u k = sin ( (2k + 1)x ) . Pravá strana f ≡ 2u 0 − u 1 − 3u 2 − 1 3 u 3 + 1 2 u 1.<br />
1. Jestliže λ /∈ V , pak právě jedno řešení.<br />
2. Pro k = 0,1,2,3 je (u k ,f) ≠ 0, tedy pro λ = 1,9,25,49 úloha nemá řešení.<br />
3. Jestliže λ ∈ V \ {1,9,25,49}, pak úloha má nekonečně mnoho řešení.<br />
6 Obecně (k+1/2)2 π 2<br />
(b−a)<br />
, vlastní funkce u 2<br />
k (x) = sin (k+1/2)π(x−a)<br />
b−a<br />
, kde k = 0, 1, 2, . . .<br />
37
Příklad 8.7: Zjistěte, jak závisí počet řešení na parametru λ ∈ R v úloze<br />
u ′′ + λu = − 1 3 sin(−2x) + 7sin 6x − 1 9 sin 14x + 5sin(−18x) − 2 7 sin(−22x),<br />
Nezapomeňte své závěry řádně zdůvodnit.<br />
u(0) = u ′ (π/4) = 0.<br />
Řešení: Vlastní čísla jsou 7 V ≡ {4(2k + 1) 2 : k = 0,1,2,... }, vlastní funkce příslušná k λ =<br />
4(2k + 1) 2 je u k = sin ( 2(2k + 1)x ) . Pravá strana f ≡ 1 3 u 0 + 7u 1 − 1 9 u 3 − 5u 4 + 2 7 u 5.<br />
1. Jestliže λ /∈ V , pak právě jedno řešení.<br />
2. Pro k = 0,1,3,4,5 je (u k ,f) ≠ 0, tedy pro λ = 4,36,196,324,484 úloha nemá řešení.<br />
3. Jestliže λ ∈ V \ {4,36,196,324, 484}, pak příslušná vlastní funkce je ortogonální k f, a<br />
tudíž úloha má nekonečně mnoho řešení.<br />
Příklad 8.8: 1) Zjistěte, jak závisí počet řešení na parametru λ ∈ R v úloze<br />
u ′′ + λu = −3sin(−2x) + sin(−6x) + 2sin(18x) − 1 3 sin(−26x),<br />
u(0) = u ′ (π/4) = 0.<br />
Nezapomeňte své závěry řádně zdůvodnit.<br />
2) Je dána okrajová úloha u ′′ + 16u = f, u(−π/2) = 0 = u(π/2).<br />
Rozhodněte, zda a kolik má řešení, jestliže a) f ≡ 1; b) f ≡ x 2 .<br />
Své rozhodnutí řádně zdůvodněte (výpočtem, úvahou).<br />
Řešení: 1) Vlastní čísla jsou V ≡ {4(2k + 1) 2 : k = 0,1,2,... }, vlastní funkce příslušná<br />
k λ = 4(2k + 1) 2 je u k = sin ( 2(2k + 1)x ) . Pravá strana f ≡ 3u 0 − u 1 + 2u 4 + 1 3 u 6.<br />
1. Jestliže λ /∈ V , pak právě jedno řešení.<br />
2. Pro k = 0,1,4,6 je (u k ,f) ≠ 0, tedy pro λ = 4,36,18 2 = 324,26 2 = 676 úloha nemá<br />
řešení.<br />
3. Jestliže λ ∈ V \ {4,36,324,676}, pak příslušná vlastní funkce je ortogonální k f, a tudíž<br />
úloha má nekonečně mnoho řešení.<br />
2) Pro tuto úlohu jsou vlastní čísla dána hodnotami k 2 π2 = k 2 , kde k = 1,2,3,...<br />
(b−a) 2<br />
Hodnota 16 tedy je vlastním číslem s příslušnou vlastní funkcí<br />
= sin(4x + 2π) = sin(4x), což je lichá funkce.<br />
a) Platí (u 4 ,1) = 0, nebot’ u 4 (x) je funkce lichá na ( − π 2 , π 2)<br />
. Také (u4 ,x 2 ) = 0, nebot’ x 2 u 4 (x)<br />
je funkce lichá na ( − π 2 , π 2)<br />
. Obě úlohy mají nekonečně mnoho řešení.<br />
u 4 (x) = sin 4π(x−a)<br />
b−a<br />
7 Obecně (k+1/2)2 π 2<br />
(b−a) 2 , k = 0, 1, 2, . . ..<br />
38
9 Pozitivní definitnost operátorů<br />
V kapitolách 9, 10 a 11 se ve většině úloh požaduje nalezení symetrického a pozitivně definitního<br />
operátoru. Ukázat symetrii operátoru je snadný úkon vyžadující tři kroky: přepsání diferenciální<br />
rovnice do divergentního tvaru (není-li v tomto tvaru již zadána), definování operátoru a úpravu<br />
energetického skalárního součinu integrací po částech s využitím okrajových podmínek.<br />
Náročnější bývá dokázat pozitivní definitnost operátoru, případně správně upravit diferenciální<br />
rovnici tak, aby příslušný operátor byl pozitivně definitní. Přestože obě kapitoly nabízejí<br />
řadu ukázkových řešení, zkušenost ukazuje, že mnoho studentů s těmito úlohami zápasí — snad<br />
proto, že ukázková řešení jsou stručná nebo že se čtenářům v jednotlivých řešeních nedaří rozpoznat<br />
jednotný a vždy stejný postup. Tyto úvodní odstavce se o takový celkový pohled pokoušejí.<br />
Návod, jak se vypořádat se situacemi, s nimiž se setkáte při řešení zkouškových úloh.<br />
1. Rovnici převedeme do divergentního tvaru<br />
− ( p(x)u ′ (x) ) ′ + q(x)u(x) = f(x), (5)<br />
kde p je kladná funkce na intervalu [a,b], v jehož koncových bodech jsou zadány okrajové<br />
podmínky. Ke zjištění, zda p je kladná funkce, může být nutné určit její minimum a<br />
maximum na [a,b]. Pokud je p funkce záporná na [a,b], vynásobíme rovnici (5) číslem −1<br />
a dále pracujeme s takto upravenou rovnicí.<br />
Extrémy funkce q na [a,b] v této fázi sice nejsou důležité, ale to zda q je funkce nezáporná<br />
bude významné v kroku 4.<br />
2. Definujeme operátor<br />
a jeho definiční obor D(A); u ∈ D(A).<br />
Au ≡ − ( pu ′) ′ + qu<br />
3. Užitím metody integrace po částech a využitím okrajových podmínek ukážeme, že operátor<br />
je symetrický, tj.<br />
(Au,v) = (u,Av) = (u,v) A ≡<br />
∫ b<br />
a<br />
pu ′ v ′ dx +<br />
∫ b<br />
a<br />
quv dx ∀u,v ∈ D(A). (6)<br />
4. Dokážeme pozitivní definitnost operátoru A. Nejčastěji jste se setkali s verzí (o jiné<br />
možnosti pojednává bod 6)<br />
∀u ∈ D(A) (u,u) A ≥ c<br />
∫ b<br />
kde c je kladná konstanta nezávislá na u ∈ D(A).<br />
a<br />
u 2 dx = c‖u‖ 2 L 2 (a,b) , (7)<br />
a) Pokud p a q jsou na [a,b] kladné funkce, postačí jednoduchý odhad založený na nerovnostech<br />
(u,u) A ≥<br />
∫ b<br />
a<br />
quv dx ≥ c<br />
∫ b<br />
a<br />
uv dx,<br />
kde kladná konstanta c je odvozena na základě minimalizace funkce q na intervalu [a,b].<br />
Lepší (silnější) odhad využívá i prvního integrálu v (6) (kde u = v) a Friedrichsovy<br />
nerovnosti.<br />
b) Pokud p > 0 a q = 0 na [a,b], je odhad založen na aplikaci Friedrichsovy nerovnosti na<br />
první integrál v (6) (kde samozřejmě je funkce v nahrazena funkcí u). K tomu, aby bylo<br />
39
možné použít Friedrichsovu nerovnost, je nejdříve nutné odhadnout hodnotu integrálu<br />
zdola pomocí minima funkce p na [a,b].<br />
c) Pokud p > 0 a funkce q není na [a,b] nezáporná (pozor, může být záporná nebo může<br />
měnit znaménko), postupuje se jako v a), navíc je však nezbytné vhodně odhadnout i<br />
druhý integrál v (6). Pro splnění pozitivní definitnosti by odhad v tomto případě měl být<br />
takový, že ač druhý integrál odhadneme zespoda zápornou hodnotou, je součet dolního<br />
odhadu prvního integrálu a této záporné hodnoty stále ještě větší nebo roven c‖u‖ 2 , kde<br />
c > 0. Jestliže máme před druhým integrálem znaménko +, jako je tomu v (6), je odhad<br />
založen na hodnotě minima funkce q na [a,b].<br />
5. Pokud jsme omylem v (5) neověřili kladnost p nebo chybně (zbytečně) změnili znaménko<br />
rovnice, ukáže se to právě při zjišt’ování pozitivní definitnosti. První integrál totiž nebude<br />
kladný. Pak stačí rovnici a definiční předpis operátoru násobit −1 a znovu se věnovat<br />
důkazu pozitivní definitnosti, symetrie operátoru zůstane zachována.<br />
6. Pozitivní definitnost operátoru A může mít i podobu<br />
∀u ∈ D(A)<br />
(∫ b<br />
(u,u) A ≥ c u 2 dx +<br />
a<br />
∫ b<br />
a<br />
) (<br />
)<br />
u ′2 dx = c ‖u‖ 2 L 2 (a,b) + ‖u′ ‖ 2 L 2 (a,b)<br />
, (8)<br />
kde c je kladná konstanta nezávislá na u ∈ D(A). Myšlenka důkazu nerovnosti (8) je<br />
založena na rozkladu (u,u) A na součet dvou členů, například<br />
(u,u) A = α(u,u) A + β(u,u) A ,<br />
kde α,β > 0, přičemž α + β = 1; postačí zvolit α = β = 1/2. Pak postupem vyloženým v<br />
bodu 4 ukážeme, že první sčítanec splňuje nerovnost (7) , tj.<br />
U druhého sčítance usilujeme o odhad<br />
Kombinací (9) a (10) dostaneme odhad (8)<br />
∫ b<br />
α(u,u) A ≥ c 1 u 2 dx. (9)<br />
a<br />
∫ b<br />
β(u,u) A ≥ c 2 u ′2 dx. (10)<br />
∫ b ∫ b<br />
(u,u) A = α(u,u) A + β(u,u) A ≥ c 1 u 2 dx + c 2 u 2 dx<br />
a<br />
a<br />
(<br />
)<br />
≥ c ‖u‖ 2 L 2 (a,b) + ‖u′ ‖ 2 L 2 (a,b)<br />
,<br />
kde c = min(c 1 ,c 2 ) > 0. V praxi je jednodušší myšlenku rozkladu uplatnit až v průběhu<br />
odhadování, a to na integrál ∫ b<br />
a u′2 dx, viz řešení příkladu 9.9, kde je též ukázáno, že<br />
vhodná volba koeficientů α a β může zlepšit (zvětšit) konstantu c.<br />
a<br />
Poznámka: Výslovně upozorňuji na to, že popis řešení úloh v kapitolách 9, 10 a 11 je většinou<br />
zkratkovitý. V mnoha případech se například hned na začátku uvádí nutnost násobit rovnici<br />
hodnotou −1, aniž by na daném intervalu byly zjištěny extrémy funkce p, z nichž se pozná,<br />
zda p je kladná či záporná funkce, či zda dokonce nemění znaménko (poslední případ by vedl k<br />
podezření, že nelze najít operátor, který by byl pozitivně definitní).<br />
40
Tato zkratkovitost je nepedagogická a je dána tím, že řešení nebyla prvotně psána pro<br />
studenty, nýbrž pro učitele opravující písemné práce. Šlo tedy o základní odvození a shrnutí<br />
výsledků, nikoli o výukově zaměřený výklad.<br />
Příklad 9.9 byl vytvořen později a je podán pedagogičtěji.<br />
Příklad 9.1: Najděte operátor příslušný okrajové úloze a jeho definiční obor. Ukažte, že lze<br />
najít operátor symetrický a pozitivně definitní; použijte normu ‖u‖ 2 ≡ ‖u‖ 2 L 2 (2,5) .<br />
u ′′ ln x + u′<br />
x<br />
− uln x = 1, u(2) = 0, u(5) = 0. (11)<br />
Řešení: Aby operátor byl pozitivně definitní, je třeba vyjít z rovnice vynásobené číslem −1, tj.<br />
definovat operátor A takto<br />
kde<br />
Au = −u ′′ ln x − u′<br />
x<br />
+ uln x, u<br />
∈ D(A),<br />
D(A) = {u ∈ C 2 ([2,5]) : u(2) = 0, u(5) = 0}.<br />
Pak (11) přejde v Au = −1, u ∈ D(A).<br />
Ještě vhodnější tvar operátoru (a samozřejmě ekvivalentní s předchozím zápisem) je<br />
Au = −(u ′ ln x) ′ + uln x,<br />
u ∈ D(A).<br />
Tento zápis je vhodný pro aplikaci integrace po částech (per partes, viz dále).<br />
Symetrie. S využitím integrace per partes a okrajových podmínek 8 se skalární součiny (Au,v)<br />
a (u,Av) upraví na stejný výraz, tj.<br />
(Au,v) =<br />
=<br />
(u,Av) =<br />
=<br />
∫ 5<br />
2<br />
∫ 5<br />
2<br />
∫ 5<br />
2<br />
∫ 5<br />
2<br />
(<br />
−(u ′ ln x) ′ + uln x ) v dx<br />
u ′ v ′ lnxdx +<br />
∫ 5<br />
2<br />
uv ln xdx<br />
(<br />
−(v ′ ln x) ′ + v ln x ) udx<br />
u ′ v ′ lnxdx +<br />
∫ 5<br />
2<br />
uv ln xdx<br />
∀u,v ∈ D(A),<br />
∀u,v ∈ D(A);<br />
jest (Au,v) = (u,Av).<br />
Vyšetřeme pozitivní definitnost, tj. zda ∀u ∈ D(A) (Au,u) ≥ c‖u‖ 2 L 2 (2,5), kde kladná reálná<br />
konstanta c nezávisí na u ∈ D(A).<br />
Z předchozího (pro jednoduchost ‖u‖ 2 ≡ ‖u‖ 2 L 2 (2,5) )<br />
(Au,u) =<br />
≥<br />
∫ 5<br />
2<br />
∫ 5<br />
lze tedy například zvolit c = ln 2.<br />
2<br />
∫ 5<br />
u ′2 ln xdx + u 2 lnxdx<br />
2<br />
( )<br />
min ln t (u ′2 + u 2 )dx ≥ ln 2 ( ‖u ′ ‖ 2 + ‖u‖ 2) ≥ ln 2‖u‖ 2 ,<br />
t∈[2,5]<br />
8 Využití okrajových podmínek by mělo být řádně vysvětleno, viz řešení Příkladu 9.7.<br />
41
Ještě větší c nám poskytne použití (Friedrichsovy) nerovnosti 9<br />
Pak totiž<br />
∫ b<br />
ln 2 ( (<br />
‖u ′ ‖ 2 + ‖u‖ 2) ≥ ln 2<br />
a<br />
∫<br />
u ′2 2 b<br />
dx ≥<br />
(b − a) 2 u 2 dx. (12)<br />
)<br />
2<br />
(5 − 2) 2 ‖u‖2 + ‖u‖ 2<br />
a<br />
= 11ln 2 ‖u‖ 2 .<br />
9<br />
Příklad 9.2: Jako příklad 9.1, jen s rovnicí<br />
u ′′ ln x + u′<br />
x<br />
= 1, u(2) = 0, u(5) = 0.<br />
Řešení: Stejný postup jako v příkladu 1, jen v pozitivní definitnosti se využije nerovnosti (12):<br />
∀u ∈ D(A) (Au,u) =<br />
∫ 5<br />
2<br />
u ′2 ln xdx ≥ ln 2‖u ′ ‖ 2 ≥ 2 9 ln 2‖u‖2 .<br />
Příklad 9.3: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
u ′′ e −4x<br />
20<br />
− u′ e −4x<br />
5<br />
− ue −2x = x 3 + 2, u(0) = 0, u(2) = 0.<br />
Ukažte, že lze najít operátor symetrický a takový, že pro každou funkci u z D(A) platí (Au,u) ≥<br />
c‖u‖ 2 L 2 (0,2), kde c je vhodná kladná konstanta — její velikost blíže určete.<br />
( u ′ e −4x ) ′<br />
Řešení: Operátor Au ≡ − + ue −2x s definičním oborem<br />
20<br />
D(A) = {u ∈ C 2 ([0, 2]) : u(0) = 0 = u(2)}.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek 10 )<br />
∫ [<br />
2<br />
( u ′ e −4x ) ′<br />
]<br />
(Au,v) = − + ue −2x v dx<br />
0 20<br />
∫ 2<br />
( )<br />
e<br />
−4x<br />
=<br />
0 20 u′ v ′ + e −2x uv dx ∀u,v ∈ D(A),<br />
∫ 2<br />
( )<br />
e<br />
−4x<br />
(u,Av) =<br />
20 u′ v ′ + e −2x uv dx ∀u,v ∈ D(A).<br />
0<br />
Pozitivní definitnost (ve smyslu skript [2])<br />
∫ 2<br />
( )<br />
e<br />
−4x<br />
(Au,u) =<br />
20 u′2 + e −2x u 2 dx ≥ c‖u‖ 2 L 2 (0,2) ,<br />
kde (například) c = 1/100; min x∈[0,2] e −2x = e −4 > 3 −4 > 1/100.<br />
0<br />
Příklad 9.4: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
x 2 u ′′ + 2xu ′ − usin(x) = 2cos x + 1, u(π/6) = 0, u(5π/6) = 0.<br />
9 Nerovnost platí pro u ∈ C 1 ([a, b]), přičemž u(a) = 0, viz [1, strana 112]. S touto nerovností se studenti<br />
setkají na přednášce.<br />
10 Využití okrajových podmínek by mělo být řádně vysvětleno, viz řešení Příkladu 9.7.<br />
42
Ukažte, že lze najít operátor symetrický a takový, že pro každou funkci u z D(A) platí (Au,u) ≥<br />
c‖u‖ 2 L 2 (π/6, 5π/6)<br />
, kde c je vhodná kladná konstanta — její velikost blíže určete.<br />
Řešení: Operátor Au ≡ − ( x 2 u ′) ′ + usin x s definičním oborem<br />
D(A) = {u ∈ C 2 ([π/6, 5π/6]) : u(π/6) = 0 = u(5π/6)}.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek)<br />
(Au,v) =<br />
∫ 5π/6<br />
π/6<br />
Pozitivní definitnost (ve smyslu skript [2])<br />
(Au,u) =<br />
∫ 5π/6<br />
π/6<br />
kde (například) c = 1/2; min x∈[π/6,5π/6] sin x = 1/2.<br />
(<br />
x 2 u ′ v ′ + uv sinx ) dx = (u,Av) ∀u,v ∈ D(A).<br />
(<br />
x 2 u ′2 + u 2 sin x ) dx ≥ c‖u‖ 2 L 2 (π/6, 5π/6)<br />
∀u ∈ D(A),<br />
Příklad 9.5: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
(1 + ln x)u ′′ + u′<br />
x − ue−x = 2sin x, u(1) = 0, u(2) = 0.<br />
Ukažte, že lze najít operátor symetrický a takový, že pro každou funkci u z D(A) platí (Au,u) ≥<br />
c‖u‖ 2 L 2 (1,2), kde c je vhodná kladná konstanta — její velikost blíže určete.<br />
Řešení: Operátor Au ≡ − ((1 + ln x)u ′ ) ′ + ue −x s definičním oborem<br />
D(A) = {u ∈ C 2 ([1, 2]) : u(1) = 0 = u(2)}.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek)<br />
(Au,v) =<br />
∫ 2<br />
Pozitivní definitnost (ve smyslu skript [2])<br />
(Au,u) =<br />
1<br />
∫ 2<br />
1<br />
(<br />
(1 + ln x)u ′ v ′ + e −x uv ) dx = (u,Av) ∀u,v ∈ D(A).<br />
(<br />
(1 + ln x)u ′2 + e −x u 2) dx ≥ c‖u‖ 2 L 2 (1,2)<br />
∀u ∈ D(A),<br />
kde (například) c = 1/10, nebot’ min x∈[1,2] e −x = e −2 > 3 −2 > 1/10.<br />
Příklad 9.6: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
(1 + cos x)e −x u ′′ − (1 + cos x + sinx)e −x u ′ = ln(x + 5), u(0) = 0, u(π/2) = 0. (13)<br />
Ukažte, že lze najít operátor symetrický a takový, že pro každou funkci u z D(A) platí (Au,u) ≥<br />
c‖u‖ 2 L 2 (0,π/2), kde c je vhodná kladná konstanta — její velikost blíže určete. Pro tento operátor<br />
napište okrajovou úlohu (13) v operátorovém tvaru. Může být c > 1/10 (Při výpočtech můžete<br />
použít e π ≈ 25, e π/2 ≈ 5, e ≈ 2,7, π 2 ≈ 10.)<br />
Řešení: Operátor Au ≡ − ((1 + cos x)e −x u ′ ) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0, π/2]) : u(0) = 0 = u(π/2)}.<br />
Operátorová úloha: Najít funkci u ∈ D(A) takovou, aby platilo<br />
Au = − ln(x + 5).<br />
43
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek — zdůvodnění!)<br />
(Au,v) =<br />
∫ π/2<br />
Pozitivní definitnost (ve smyslu skript [2])<br />
(Au,u) =<br />
0<br />
∫ π/2<br />
0<br />
(1 + cos x)e −x u ′ v ′ dx = (u,Av) ∀u,v ∈ D(A).<br />
(1 + cos x)e −x u ′2 dx ≥ c‖u‖ 2 L 2 (0,π/2)<br />
∀u ∈ D(A),<br />
kde (například) c = 8/(5π 2 ), nebot’ min x∈[0,π/2] (1 + cos x)e −x = e −π/2 ≥ 1/5 a dále lze využít<br />
nerovnosti (12) (tu studenti mají znát), tj.<br />
∫ b<br />
a<br />
u ′2 dx ≥<br />
∫<br />
2 b<br />
(b − a) 2 u 2 dx, kde máme<br />
a<br />
2<br />
(b − a) 2 = 8 π 2.<br />
Ano, c = 8/(5π 2 ) ≈ 0.16 > 1/10.<br />
Příklad 9.7: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
(<br />
− 1 3 e2x + sin 2x ) ( 2<br />
u ′′ −<br />
3 3 e2x − 2 3 cos 2x )<br />
u ′ − 1 u = 2sin x,<br />
3 12π2 u(0) = 0, u ′ (π) = 0.<br />
Ukažte, že lze najít operátor symetrický a takový, že pro každou funkci u z D(A) platí (Au,u) ≥<br />
c‖u‖ 2 L 2 (0,π) , odvod ’te konkrétní velikost konstanty c ∈ R. Napište operátorovou rovnici.<br />
Řešení: Zadaný operátor je pozitivně definitní, není třeba měnit znaménko.<br />
Divergentní tvar operátoru<br />
Au ≡ (( − 1 3 e2x + sin 2x )<br />
3 u<br />
′ ) ′ −<br />
1<br />
12π<br />
u 2<br />
s definičním oborem D(A) = {u ∈ C 2 ([1, π]) : u(0) = 0 = u ′ (π)}.<br />
Operátorová rovnice: najít takový prvek u ∈ D(A), aby Au = 2sin x.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek), pro u,v ∈ D(A)<br />
∫ π<br />
[((<br />
(Au,v) = − 1<br />
0 3 e2x + sin 2x 3<br />
[(<br />
= − 1 3 e2x + sin 2x )<br />
u ′ v<br />
3<br />
∫ π<br />
( 1<br />
=<br />
3 e2x − sin 2x 3<br />
0<br />
)<br />
u ′ ) ′<br />
− 1<br />
] π<br />
0<br />
∫ π<br />
−<br />
)<br />
u ′ v ′ dx −<br />
0<br />
∫ π<br />
]<br />
12π 2 u v dx<br />
(<br />
− 1 3 e2x + sin 2x 3<br />
0<br />
1<br />
12π2uv dx.<br />
Studenti mají zdůvodnit nulovost členu<br />
[(<br />
− 1 3 e2x + sin 2x ) ] π<br />
u ′ v<br />
3<br />
0<br />
) ∫ π<br />
u ′ v ′ dx −<br />
0<br />
1<br />
uv dx<br />
12π2 odkazem na v(0) = 0 a u ′ (π) = 0. Jinak strhávejte body.<br />
Podobně (u,Av). Operátor je symetrický.<br />
44
Pozitivní definitnost (ve smyslu skript [2], s využitím nerovnosti (12))<br />
∫ π<br />
( 1<br />
(Au,u) =<br />
0 3 e2x − sin 2x ) ∫ π<br />
u ′2 1<br />
dx −<br />
3<br />
0 12π 2u2 dx<br />
∫ π<br />
( ( 1<br />
≥ min<br />
0 t∈[0,π] 3 e2t − sin 2t )) ∫ π<br />
u ′2 1<br />
dx −<br />
3<br />
0 12π 2u2 dx<br />
= 1 ∫ π ∫ π<br />
u ′2 1<br />
dx −<br />
3 0 0 12π 2 u2 dx<br />
≥ 2 ∫ π ∫ π<br />
3π 2 u 2 1<br />
dx −<br />
12π 2 u2 dx<br />
0<br />
= 7<br />
12π 2 ∫ π<br />
0<br />
u 2 dx.<br />
0<br />
Hledaná konstanta c = 7<br />
12π 2 .<br />
Studenti mají zdůvodnit, proč je minimum rovno 1/3 (derivace výrazu je nezáporná, je to<br />
rostoucí funkce, minima se nabývá v t = 0). Chybějící zdůvodnění = bodová ztráta.<br />
Příklad 9.8: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
( 1<br />
3 x3 + 6x 2 + 11x + 46 3<br />
)<br />
u ′′ + ( x 2 + 12x + 11 ) u ′ + 2 9 u = 5cos3 x,<br />
u(−3) = 0, u ′ (0) = 0.<br />
Ukažte, že je možné tento operátor zvolit symetrický a zároveň takový, že lze nalézt konstantu<br />
c > 0 takovou, že pro každou funkci u z D(A) platí (Au,u) ≥ c‖u‖ 2 L 2 (−3,0) . Odvod ’te konkrétní<br />
hodnotu konstanty c. Napište operátorovou rovnici. Jednotlivé kroky řádně zdůvodněte.<br />
Řešení: Operátor odvozený přímo z levé strany rovnice není pozitivně definitní, je třeba změnit<br />
znaménko. Studenti by na to měli přijít nejpozději při zjišt’ování pozitivní definitnosti.<br />
Pozitivně definitní operátor 11 v divergentním tvaru<br />
)<br />
u<br />
′ ) ′ −<br />
2<br />
9 u<br />
Au ≡ − (( 1<br />
3 x3 + 6x 2 + 11x + 46 3<br />
s definičním oborem D(A) = {u ∈ C 2 ([−3, 0]) : u(−3) = 0 = u ′ (0)}.<br />
Operátorová rovnice: najít takový prvek u ∈ D(A), aby Au = −5cos 3 x.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek), pro u,v ∈ D(A)<br />
(Au,v) =<br />
∫ 0<br />
= −<br />
=<br />
−3<br />
− 2 9<br />
∫ 0<br />
[ (( 1<br />
−<br />
3 x3 + 6x 2 + 11x + 46 ) ′ )u ′ − 2 ]<br />
3 9 u v dx<br />
[( 1<br />
3 x3 + 6x 2 + 11x + 46 3<br />
)<br />
u ′ v<br />
∫ 0<br />
−3<br />
uv dx<br />
−3<br />
( 1<br />
3 x3 + 6x 2 + 11x + 46 3<br />
] 0<br />
−3<br />
∫ 0<br />
+<br />
−3<br />
)<br />
u ′ v ′ dx − 2 ∫ 0<br />
uv dx.<br />
9 −3<br />
Studenti mají zdůvodnit nulovost členu<br />
[( 1<br />
3 x3 + 6x 2 + 11x + 46 ) ] 0<br />
u ′ v<br />
3<br />
−3<br />
( 1<br />
3 x3 + 6x 2 + 11x + 46 )<br />
u ′ v ′ dx<br />
3<br />
11 Na intervalu [−3, 0] má výraz 1 3 x3 + 6x 2 + 11x + 46<br />
3 minimum 10 a maximum 82 3<br />
, výraz je tedy<br />
na celém intervalu [−3, 0] kladný, pro naše potřeby je nutné vynásobit celou rovnici číslem −1. Postup<br />
nalezení extrémů je ukázán v závěru řešení.<br />
45
odkazem na v(−3) = 0 a u ′ (0) = 0. Jinak strhávejte body.<br />
Podobně (u,Av). Operátor je symetrický.<br />
Pozitivní definitnost 12 (ve smyslu skript [2])<br />
(Au,u) =<br />
≥<br />
∫ 0<br />
( 1<br />
−3 3 x3 + 6x 2 + 11x + 46 3<br />
( ( 1<br />
min<br />
t∈[−3,0] 3 t3 + 6t 2 + 11t + 46 3<br />
∫ 0<br />
= 10<br />
≥ 20<br />
9<br />
= 2<br />
−3<br />
∫ 0<br />
∫ 0<br />
−3<br />
u ′2 dx − 2 9<br />
∫ 0<br />
−3<br />
−3<br />
u 2 dx − 2 9<br />
u 2 dx.<br />
Hledaná konstanta c = 2 nebo c ∈ (0,2].<br />
Minimalizace<br />
je standardní. Ze vztahu<br />
získáme t = −1. Jest<br />
∫ 0<br />
−3<br />
∫ 0<br />
−3<br />
u 2 dx<br />
u 2 dx<br />
) ∫ 0<br />
u ′2 dx −<br />
−3<br />
2<br />
9 u2 dx<br />
))<br />
u ′2 dx − 2 9<br />
min<br />
t∈[−3,0] g(t), kde g(t) = ( 1<br />
3 t3 + 6t 2 + 11t + 46 3<br />
g ′ (t) = t 2 + 12t + 11 = (t + 1)(t + 11) = 0<br />
g(−3) = −9 + 54 − 33 + 46 3 = 82 3 ,<br />
)<br />
∫ 0<br />
−3<br />
u 2 dx<br />
g(−1) = − 1 3 + 6 − 11 + 46 3 = 30 3<br />
= 10 ⇒ minimum,<br />
g(0) = 46 3 .<br />
Příklad 9.9: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
(−3x 3 + 15x 2 − 51 ) (<br />
4 x + 6 u ′′ + −9x 2 + 30x − 51 ) (<br />
u ′ + x − 1 )<br />
u = sinx,<br />
4 2<br />
u(0) = 0, u(1) = 0.<br />
Ukažte, že je možné tento operátor zvolit ( symetrický a zároveň)<br />
takový, že lze nalézt konstantu<br />
c > 0 takovou, že platí (Au,u) ≥ c ‖u‖ 2 L 2 (0,1) + ‖u′ ‖ 2 L 2 (0,1)<br />
pro každou funkci u z D(A).<br />
Odvod’te konkrétní hodnotu konstanty c. Napište operátorovou rovnici. Jednotlivé kroky řádně<br />
zdůvodněte.<br />
Řešení: Zadaná rovnice v divergentním tvaru −(pu ′ ) ′ + qu = f:<br />
−<br />
((3x 3 − 15x 2 + 51 ) ) ′ (<br />
4 x − 6 u ′ + x − 1 )<br />
u = sin x.<br />
2<br />
12 Využito ∫ b<br />
a u′2 dx ≥ 2<br />
(b−a) 2 ∫ b<br />
a u2 dx. Minimalizace použitá při odhadování integrálu je popsána dále.<br />
46
Pro pozitivní definitnost příslušného operátoru potřebujeme, aby funkce<br />
p(x) = ( 3x 3 − 15x 2 + 51<br />
4 x − 6) byla kladná na intervalu [0,1]. Najdeme její extrémy na intervalu<br />
[0,1].<br />
Ukáže se, že p ′ (x) = 9x 2 − 30x + 51<br />
17<br />
4<br />
= 0, je-li x =<br />
6 nebo x = 1 2<br />
. Extrémy na [0,1] tedy<br />
mohou nastat v bodech 0, 1 2<br />
a 1. Hodnoty funkce<br />
( 1<br />
p(0) = −6, p = −3, p(1) = −<br />
2)<br />
21 4<br />
ukazují, že funkce p je na [0,1] záporná a že můžeme očekávat, že pozitivně definitní operátor 13<br />
bude přímo odvozen od původní rovnice vynásobené číslem −1. V této fázi lze hovořit jen o<br />
očekávání, pozitivní definitnost ještě není dokázána, ve hře je totiž ještě funkce q.<br />
Definujme operátor A předpisem<br />
Au ≡ −<br />
((−3x 3 + 15x 2 − 51 ) ) ′ (<br />
4 x + 6 u ′ − x − 1 )<br />
u,<br />
2<br />
kde u ∈ D(A) = { u ∈ C 2 ([0,1]) : u(0) = 0 = u(1) } .<br />
Operátor A je symetrický, což se dokáže standardně integrací po částech a využitím okrajových<br />
podmínek.<br />
Při dokazování silnější verze pozitivní definitnosti, jež je požadována v zadání úlohy, postupujeme<br />
zcela standardně, jen v okamžiku před aplikací Friedrichsovy nerovnosti rozdělíme<br />
integrál ∫ 1<br />
0 u′2 dx na součet dvou integrálů 14 a Friedrichsovu nerovnost uplatníme jen na jeden<br />
z nich. Navíc známe extrémy funkce 3t 3 −15t 2 + 51<br />
4<br />
t −6 na intervalu [0,1], což se nám nyní hodí<br />
(pozor na znaménko hodnoty minima).<br />
(Au,u) =<br />
≥<br />
= 3<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
(−3x 3 + 15x 2 − 51 4 x + 6 )<br />
u ′2 dx −<br />
(<br />
0<br />
∫ 1<br />
min<br />
t∈[0,1]<br />
u ′2 dx +<br />
∫ 1<br />
(−3t 3 + 15t 2 − 51 4 t + 6 ))<br />
u ′2 dx +<br />
∫ 1<br />
0<br />
∫ 1<br />
( 1<br />
2 − x )<br />
u 2 dx<br />
= 3 u ′2 dx + 3 u ′2 dx +<br />
2 0 2 0<br />
≥ 3 ∫<br />
2 1 ∫ 1<br />
2 (1 − 0) 2 u 2 dx +<br />
0 0<br />
∫ 1 ∫ 1<br />
(<br />
≥ 3 u 2 dx + min<br />
= 3<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
u 2 dx − 1 2<br />
= 5 u 2 dx + 3 2 0 2<br />
≥ 3 (∫ 1<br />
u 2 dx +<br />
2<br />
0<br />
0 t∈[0,1]<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
u 2 dx + 3 2<br />
u ′2 dx<br />
)<br />
u ′2 dx .<br />
∫ 1<br />
0<br />
0<br />
( 1<br />
2 − x )<br />
u 2 dx<br />
( 1<br />
2 − x )<br />
u 2 dx + 3 2<br />
( 1<br />
2 − t ))<br />
u 2 dx + 3 2<br />
∫ 1<br />
0<br />
u ′2 dx<br />
(<br />
x − 1 )<br />
u 2 dx<br />
2<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
( 1<br />
2 − x )<br />
u 2 dx<br />
u ′2 dx<br />
u ′2 dx<br />
13 Nerovnost v zadání představuje silnější požadavek, než je ta verze pozitivní definitnosti, s níž se<br />
obvykle setkáváte. Uvidíme však, že ji dokážeme obvyklým postupem, jen navíc použijeme drobný trik.<br />
14 Viz přechod od 3. ke 4. řádku v řetězci rovností a nerovností níže; důvod je vysvětlen v úvodu této<br />
kapitoly (bod 6).<br />
47
Hledanou konstantu c tedy můžeme volit např. takto: c ∈ (0,3/2]. Horní mez pro konstantu c<br />
lze zvýšit vhodnějším rozdělením integrálu. Například volba<br />
∫ 1<br />
0<br />
u ′2 dx = 7<br />
18<br />
∫ 1<br />
0<br />
u ′2 dx + 11<br />
18<br />
∫ 1<br />
0<br />
u ′2 dx<br />
s uplatněním Friedrichsovy nerovnosti na první integrál vpravo by nás přivedla k c ∈ (0,11/6].<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo<br />
Au = − sinx.<br />
10 Pozitivní definitnost operátorů,<br />
Ritzova metoda<br />
Doporučuji přečíst si text na začátku předchozí kapitoly a věnovat pozornost i obtížnějším<br />
příkladům 9.8 a 9.9.<br />
Příklad 10.1: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(4x 2 − 4x + 8)u ′′ + (8x − 4)u ′ = −π cos 4 x, (14)<br />
u(0) = 0, u(π) = 0. (15)<br />
S použitím nalezeného operátoru napište okrajovou úlohu (14)-(15) jako operátorovou rovnici.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (0,π), kde c je kladná konstanta, tuto konstantu konkretizujte. Lze zaručit, že c > 6/5<br />
Ritzovou metodou pak najděte přibližné řešení okrajové úlohy s operátorem A. Ritzovu aproximaci<br />
hledejte ve tvaru w = asin x, kde a ∈ R. (Pro usnadnění výpočtů: ∫ π<br />
0 cos2 xdx = π<br />
∫<br />
2 ,<br />
π<br />
0 xcos2 xdx = π2<br />
4 , ∫ π<br />
0 x2 cos 2 xdx = π3<br />
6 + π 4 .)<br />
Řešení: Operátor Au ≡ −4 ( (x 2 − x + 2)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,π]) : u(0) = 0 = u(π)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo (znaménka!)<br />
−4 ( (x 2 − x + 2)u ′) ′<br />
= π cos 4 x.<br />
Symetrie (integrace po částech, role okrajových podmínek 15 )<br />
(Au,v) = 4<br />
∫ π<br />
0<br />
(x 2 − x + 2)u ′ v ′ dx = 4<br />
Pozitivní definitnost (ve smyslu skript [2]) 16<br />
(Av,v) = 4<br />
≥ 7<br />
∫ π<br />
0<br />
∫ π<br />
0<br />
(x 2 − x + 2)v ′2 dx ≥ 4<br />
∫ π<br />
v ′2 dx ≥ 7 2 π 2 ‖v‖2 L 2 (0,π) ,<br />
0<br />
∫ π<br />
0<br />
(x 2 − x + 2)v ′ u ′ dx = (u,Av).<br />
(<br />
)<br />
min<br />
t∈[0,π] (t2 − t + 2) v ′2 dx<br />
15 V písemce je nutné konkrétně zdůvodnit, proč člen [ (x 2 − x + 2)u ′ (x)v(x) ] π<br />
je roven nule. Je to<br />
0<br />
důsledek rovnosti v(0) = 0 = v(π) zavedené v množině D(A), do níž patří jak u, tak v. Pozor, pro<br />
u ∈ D(A) obecně u ′ (0) ≠ 0 ≠ u ′ (π).<br />
16 Studenti by měli znát Friedrichsovu nerovnost (12).<br />
48
tedy c = 14<br />
π 2 > 14/10 > 6/5.<br />
Z podmínky minima funkcionálu energie plyne<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
kde f = π cos 4 x a ω = sin x. Jest (v prvním integrálu použijeme substituci cos x = t, v druhém<br />
integrálu využijeme rovnosti uvedené v zadání úlohy)<br />
(f,ω) =<br />
∫ π<br />
0<br />
∫ 1<br />
[ t<br />
π cos 4 xsin xdx = π t 4 5] 1<br />
dt = π = 2<br />
−1 5<br />
−1<br />
5 π.<br />
(Aω,ω) = 4<br />
= 4<br />
∫ π<br />
0<br />
(x 2 − x + 2)cos 2 xdx<br />
( ) π<br />
4 + π3<br />
6 − π2<br />
4 + 2π = 2π3<br />
2 3 − π2 + 5π.<br />
Odtud a =<br />
2<br />
5<br />
2<br />
3 π2 − π + 5 , a tedy w(x) = 6<br />
10π 2 sinx, kde x ∈ [0,π].<br />
− 15π + 75<br />
Příklad 10.2: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(x 2 + 4)u ′′ + 2xu ′ = −x 2 , (16)<br />
u(−1) = 0, u(1) = 0. (17)<br />
S použitím nalezeného operátoru napište okrajovou úlohu (16)-(17) jako operátorovou rovnici.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (−1,1), kde c je kladná konstanta, tuto konstantu konkretizujte. Ritzovou metodou pak<br />
najděte přibližné řešení okrajové úlohy s operátorem A. Ritzovu aproximaci hledejte ve tvaru<br />
w = a(x + 1)(x − 1), kde a ∈ R.<br />
Řešení: Operátor Au ≡ − ( (x 2 + 4)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([−1,1]) : u(−1) = 0 = u(1)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo (znaménka!)<br />
− ( (x 2 + 4)u ′) ′<br />
= x 2 .<br />
Symetrie (integrace po částech, využití okrajových podmínek 17 ).<br />
Pozitivní definitnost (ve smyslu skript [2]) 18<br />
(Av,v) ≥ 4 2 2 2 ‖v‖2 L 2 (−1,1) ,<br />
tedy c = 2.<br />
Z podmínky minima funkcionálu energie plyne<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
17 Řádně ukázat a zdůvodnit!!! Viz poznámku k Příkladu 10.1<br />
18 Studenti by měli znát Friedrichsovu nerovnost (12).<br />
49
kde f = x 2 a ω = x 2 − 1. Jest<br />
(f,ω) =<br />
∫ 1<br />
−1<br />
x 2 (x 2 − 1)dx =<br />
∫ 1<br />
−1<br />
[ x<br />
(x 4 − x 2 5<br />
)dx =<br />
5 − x3<br />
3<br />
] 1<br />
−1<br />
= 2 5 − 2 3 = − 4 15 .<br />
(Aω,ω) =<br />
∫ 1<br />
−1<br />
(x 2 + 4)(ω ′ ) 2 dx =<br />
[ 4<br />
=<br />
5 x5 + 16 ] 1<br />
3 x3 −1<br />
∫ 1<br />
−1<br />
(x 2 + 4)4x 2 dx =<br />
= 8 5 + 32 3 = 184<br />
15 .<br />
Odtud a = −1/46. Přibližné řešení w(x) = (1 − x 2 )/46, kde x ∈ [−1,1].<br />
∫ 1<br />
−1<br />
(4x 4 + 16x 2 )dx<br />
Příklad 10.3: Stanovte operátor (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
−(1/2 + x)u ′′ − u ′ = x,<br />
u(0) = 0, u(1) = 0;<br />
ukažte, že je symetrický a že pro každou funkci v ∈ D(A) platí (Av,v) ≥ 1 2 ‖v′ ‖ 2 L 2 (0,1) (nezapomeňte<br />
na zdůvodnění). Pak Ritzovou metodou najděte přibližné řešení okrajové úlohy. Ritzovu<br />
aproximaci hledejte ve tvaru w = ax(x − 1). (Pro operátor platí i (Av,v) ≥ ˜c‖v‖ 2 L 2 (0,1), ˜c > 0,<br />
což ale nemusíte dokazovat. 19 )<br />
Řešení: Operátor Au ≡ − ((1/2 + x)u ′ ) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,1]) : u(0) = 0 = u(1)}.<br />
Symetrie (pomocí integrace po částech a s využitím okrajových podmínek), dále<br />
(Av,v) ≥ 1 2<br />
∫ 1<br />
0<br />
v ′2 dx<br />
∀v ∈ D(A).<br />
Z podmínky minima funkcionálu energie plyne 20<br />
kde f = x a ω = x(x − 1). Jest<br />
(f,ω) =<br />
∫ 1<br />
0<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
[ x<br />
(x 3 − x 2 4<br />
)dx =<br />
4 − x3<br />
3<br />
] 1<br />
0<br />
= − 1<br />
12 .<br />
(Aω,ω) =<br />
=<br />
=<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
(1/2 + x) ( (x(x − 1)) ′) 2 dx<br />
(1/2 + x)(2x − 1) 2 dx =<br />
∫ 1<br />
(4x 3 − 2x 2 − x + 1/2)dx =<br />
Odtud a = −1/4. Přibližné řešení w = −x(x − 1)/4 = (x − x 2 )/4.<br />
0<br />
(1/2 + x)(4x 2 − 4x + 1)dx<br />
[x 4 − 2x3<br />
3 − x2<br />
2 + x 1<br />
= 1/3.<br />
2]<br />
0<br />
19 Úloha je z období, kdy se ještě studentům tajila nerovnost (12). S její pomocí určíte i vhodnou<br />
konstantu ˜c.<br />
20 Studenti nemusejí odvozovat, mohou přímo použít vztah pro a.<br />
50
Příklad 10.4: Stanovte operátor (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
−(1 + x)u ′′ − u ′ = x 2 ,<br />
u(0) = 0, u(1) = 0.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (0,1), kde c je kladná konstanta, tuto konstantu konkretizujte. Ritzovou metodou pak<br />
najděte přibližné řešení okrajové úlohy. Ritzovu aproximaci hledejte ve tvaru w = ax(x − 1).<br />
Řešení: Operátor Au ≡ − ((1 + x)u ′ ) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,1]) : u(0) = 0 = u(1)}.<br />
Symetrie (zdůvodnění!)<br />
(Au,v) =<br />
∫ 1<br />
0<br />
(1 + x)u ′ v ′ dx =<br />
∫ 1<br />
0<br />
(1 + x)v ′ u ′ dx = (u,Av),<br />
Pozitivní definitnost (ve smyslu skript [2], s užitím (12))<br />
∫ 1<br />
∫ 1<br />
( )<br />
(Av,v) = (1 + x)v ′2 dx ≥ min (1 + t) v ′2 dx ≥<br />
t∈[0,1]<br />
0<br />
tedy c = 2.<br />
Z podmínky minima funkcionálu energie plyne<br />
0<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
∫ 1<br />
0<br />
v ′2 dx ≥ 2‖v‖ 2 L 2 (1,2) ,<br />
kde f = x 2 a ω = x(x −1). Odtud a = −1/10. Přibližné řešení w = −x(x −1)/10 = (x −x 2 )/10.<br />
Příklad 10.5: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(x 2 − 2x + 4)u ′′ + (2x − 2)u ′ = −x,<br />
u(0) = 0, u(2) = 0.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (0,2), kde c je kladná konstanta, tuto konstantu konkretizujte. Ritzovou metodou pak<br />
najděte přibližné řešení okrajové úlohy s operátorem A. Ritzovu aproximaci hledejte ve tvaru<br />
w = ax(2 − x), kde a ∈ R.<br />
Řešení: Operátor Au ≡ − ( (x 2 − 2x + 4)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,2]) : u(0) = 0 = u(2)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo<br />
− ( (x 2 − 2x + 4)u ′) ′<br />
= x.<br />
Symetrie (role okrajových podmínek!).<br />
Pozitivní definitnost (ve smyslu skript [2]), 21 c = 3/2 (například).<br />
Z podmínky minima funkcionálu energie plyne<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
21 Studenti by měli umět najít minimum funkce x 2 − 2x + 4 na intervalu [0, 2] (nabývá se v x = 1)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b 2 ∫ b<br />
a v′2 dx ≥<br />
(b − a) 2 a v2 dx.<br />
51
kde f = x a ω = x(2 −x). Odtud a = 5/36. Přibližné řešení w = 5x(2 −x)/36 = (10x −5x 2 )/36.<br />
Příklad 10.6: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(2 − sin 3 x)u ′′ − 3sin 2 xcos xu ′ = − cos 2 x,<br />
u(0) = 0, u(π) = 0.<br />
Zformulujte příslušnou operátorovu rovnici. Ukažte, že operátor je symetrický na D(A) a že<br />
pro každou funkci v ∈ D(A) platí (Av,v) ≥ c‖v‖ 2 L 2 (0,π), kde c je kladná konstanta, tuto konstantu<br />
konkretizujte. Ritzovou metodou pak najděte přibližné řešení okrajové úlohy s operátorem<br />
A. Ritzovu aproximaci hledejte ve tvaru w = asin x, kde a ∈ R. (Pro usnadnění výpočtů:<br />
∫ π/2<br />
0<br />
cos 2 xdx = ∫ π/2<br />
0<br />
sin 2 xdx = π 4 .)<br />
Řešení: Operátor Au ≡ − ( (2 − sin 3 x)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,π]) : u(0) = 0 = u(π)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo<br />
Au = cos 2 x.<br />
Symetrie (role okrajových podmínek!). Pozitivní definitnost (ve smyslu skript [2]), 22 c = 2<br />
π 2<br />
(například).<br />
Z podmínky minima funkcionálu energie plyne<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
kde f = cos 2 x a ω = sin x. Integrály počítáme substituční metodou, částečně lze použít vztahy<br />
pro usnadnění výpočtů, pozor však na správnou délku integračního intervalu!!! Jest<br />
∫ π<br />
∫ 1<br />
[ t<br />
(f,ω) = cos 2 xsin xdx = t 2 3] 1<br />
dt = = 2<br />
0<br />
−1 3<br />
−1<br />
3 .<br />
Odtud<br />
(Aω,ω) =<br />
∫ π<br />
0<br />
= π −<br />
(2 − sin 3 x)cos 2 xdx = 2 π ∫ π<br />
2 − (1 − cos 2 x)cos 2 xsin xdx<br />
∫ 1<br />
−1<br />
Přibližné řešení w = 10sin x<br />
15π − 4 .<br />
[ ] t<br />
(1 − t 2 )t 2 3 1<br />
dt = π −<br />
3 − t5 5<br />
−1<br />
a =<br />
2<br />
3<br />
π − 4<br />
15<br />
0<br />
= 10<br />
15π − 4 .<br />
= π − 4<br />
15 .<br />
Příklad 10.7: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(2x 2 − 4x + 5)u ′′ + (4x − 4)u ′ = −x 2 ,<br />
u(−1) = 0, u(2) = 0.<br />
22 Studenti by měli umět najít minimum funkce 2 − sin 3 x na intervalu [0, π] (nabývá se v x = π/2)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b 2 ∫ b<br />
a v′2 dx ≥<br />
(b − a) 2 a v2 dx.<br />
52
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (−1,2), kde c je kladná konstanta, tuto konstantu konkretizujte. Ritzovou metodou pak<br />
najděte přibližné řešení okrajové úlohy s operátorem A. Ritzovu aproximaci hledejte ve tvaru<br />
w = a(x + 1)(x − 2), kde a ∈ R.<br />
Řešení: Operátor Au ≡ − ( (2x 2 − 4x + 5)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([−1,2]) : u(−1) = 0 = u(2)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo<br />
Symetrie (role okrajových podmínek!)<br />
(Au,v) =<br />
∫ 2<br />
−1<br />
Au = x 2 .<br />
(2x 2 − 4x + 5)u ′ v ′ dx =<br />
Pozitivní definitnost (ve smyslu skript [2]) 23<br />
(Av,v) =<br />
≥ 3<br />
∫ 2<br />
−1<br />
∫ 2<br />
(2x 2 − 4x + 5)v ′2 dx ≥<br />
−1<br />
∫ 2<br />
v ′2 dx ≥ 3 2 3 2 ‖v‖2 L 2 (1,2) ,<br />
tedy c = 2/3.<br />
Z podmínky minima funkcionálu energie plyne<br />
−1<br />
∫ 2<br />
−1<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
−63<br />
20<br />
279<br />
5<br />
(2x 2 − 4x + 5)v ′ u ′ dx = (u,Av).<br />
(<br />
)<br />
min<br />
t∈[−1,2] (2t2 − 4t + 5) v ′2 dx<br />
kde f = x 2 a ω = (x + 1)(x − 2). Odtud a = = −63<br />
4 · 279 = −7<br />
124 .<br />
Přibližné řešení w = −7(x + 1)(x − 2)/124 = (−7x 2 + 7x + 14)/124.<br />
Příklad 10.8: Najděte pozitivně definitní operátor A (včetně definičního oboru D(A)) příslušný<br />
okrajové úloze<br />
(x 2 − 2x + 6)u ′′ + (2x − 2)u ′ = −π cos 2 x,<br />
u(0) = 0, u(π) = 0.<br />
S použitím nalezeného operátoru napište okrajovou úlohu jako operátorovou rovnici.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (0,π), kde c je kladná konstanta, tuto konstantu konkretizujte. Lze zaručit, že c > 1<br />
Ritzovou metodou pak najděte přibližné řešení okrajové úlohy s operátorem A. Ritzovu aproximaci<br />
hledejte ve tvaru w = asin x, kde a ∈ R. (Pro usnadnění výpočtů: ∫ π<br />
0 cos2 xdx = π<br />
∫<br />
2 ,<br />
π<br />
0 xcos2 xdx = π2<br />
4 , ∫ π<br />
0 x2 cos 2 xdx = π3<br />
6 + π 4 .)<br />
Řešení: Operátor Au ≡ − ( (x 2 − 2x + 6)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,π]) : u(0) = 0 = u(π)}.<br />
Operátorová rovnice: najít takovou funkci u ∈ D(A), aby platilo (znaménko!)<br />
Au = π cos 2 x.<br />
23 Studenti by měli umět najít minimum funkce 2x 2 − 4x + 5 na intervalu [−1, 2] (nabývá se v x = 1)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b 2 ∫ b<br />
a v′2 dx ≥<br />
(b − a) 2 a v2 dx.<br />
53
Symetrie (role okrajových podmínek!). Pozitivní definitnost (ve smyslu skript [2]), 24 c =<br />
10<br />
> 1.<br />
π 2 Z podmínky minima funkcionálu energie plyne<br />
a = (f,ω)<br />
(Aω,ω) ,<br />
kde f = π cos 2 x a ω = sin x. Odtud (použijeme substituční metodu a integrály ze zadání úlohy)<br />
8<br />
a =<br />
2π 2 − 6π + 39 .<br />
Příklad 10.9: Okrajovou úlohu<br />
(8x 3 − 12x 2 + 6x − 7)u ′′ (x) + (24x 2 − 24x + 6)u ′ (x) − 3 u(x) = 3,<br />
2<br />
u(0) = 0, u ′ (1) = 0,<br />
lze, pro jistý operátor A, napsat v operátorovém tvaru: najít u ∈ D(A), aby Au = f, kde f = 3,<br />
případně f = −3. Úkoly:<br />
1) Stanovte D(A) a najděte takový operátor A, aby byl symetrický na D(A) a splňoval ∀u ∈<br />
D(A) (Au,u) ≥ 17<br />
2 ‖u‖2 L 2 (0,1). (Podrobně vysvětlete využití okrajových podmínek. Zdůvodnění typu<br />
“po dosazení okrajových podmínek vyjde 0” je nedostačující.)<br />
2)<br />
{<br />
Ritzovou metodou najděte přibližné<br />
)<br />
řešení v prostoru<br />
}<br />
funkcí<br />
v ∈ C 2 ([0,1]) : v(x) = a<br />
(x − x2<br />
, kde a ∈ R .<br />
2<br />
Řešení: Operátor přímo odvozený z levé strany je pozitivně definitní, není tedy třeba násobit<br />
rovnici číslem −1. 25 Operátor A = ( (8x 3 − 12x 2 + 6x − 7)u ′) ′ −<br />
3<br />
2u; jeho definiční obor D(A) =<br />
{u ∈ C 2 ([0,1]) : u(0) = 0, u ′ (1) = 0}.<br />
Symetrie: ∀u,v ∈ D(A)<br />
(Au,v) =<br />
∫ 1<br />
0<br />
(<br />
(8x 3 − 12x 2 + 6x − 7)u ′) ′<br />
v dx −<br />
∫ 1<br />
= [( 8x 3 − 12x 2 + 6x − 7 ) u ′ v ] ∫ 1<br />
1<br />
0 − 0<br />
∫ 1 ∫<br />
3 1<br />
−<br />
0 2 uv dx = 0<br />
Studenti mají zdůvodnit nulovost členu<br />
0<br />
3<br />
uv dx<br />
2<br />
(<br />
8x 3 − 12x 2 + 6x − 7 ) u ′ v ′ dx<br />
(<br />
−8x 3 + 12x 2 − 6x + 7 ) u ′ v ′ dx −<br />
∫ 1<br />
[(<br />
8x 3 − 12x 2 + 6x − 7 ) u ′ v ] 1<br />
0<br />
odkazem na v(0) = 0 a u ′ (1) = 0. Jinak strhávejte body.<br />
Podobně (u,Av). Operátor je symetrický.<br />
0<br />
3<br />
uv dx.<br />
2<br />
24 Studenti by měli umět najít minimum funkce x 2 − 2x + 6 na intervalu [0, π] (nabývá se v x = 1)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b 2 ∫ b<br />
a v′2 dx ≥<br />
(b − a) 2 a v2 dx.<br />
25 Na intervalu [0, 1] je maximum funkce 8x 3 −12x 2 +6x −7 rovno −5, funkce je tedy na intervalu [0, 1]<br />
záporná.<br />
54
Pozitivní definitnost 26 (ve smyslu skript [2])<br />
(Au,u) =<br />
≥<br />
= 5<br />
∫ 1<br />
0<br />
∫ 1<br />
≥ 10 1<br />
0<br />
∫ 1<br />
(<br />
−8x 3 + 12x 2 − 6x + 7 ) ∫ 1<br />
u ′2 3<br />
dx −<br />
0 2 u2 dx<br />
(<br />
(<br />
min −8t 3 + 12t 2 − 6t + 7 )) u ′2 dx − 3<br />
t∈[0,1] 2<br />
0<br />
∫ 1<br />
0<br />
u ′2 dx − 3 2<br />
u 2 dx − 3 2<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
u 2 dx<br />
u 2 dx = 17 2<br />
∫ 1<br />
0<br />
u 2 dx.<br />
Tím je nerovnost potvrzena.<br />
Minimalizace<br />
min<br />
t∈[0,1] g(t), kde g(t) = ( −8t 3 + 12t 2 − 6t + 7 )<br />
je standardní. Ze vztahu<br />
získáme t = 1/2. Jest<br />
∫ 1<br />
0<br />
u 2 dx<br />
g ′ (t) = −24t 2 + 24t − 6 = −6(4t 2 − 4t + 1) = −6(2t − 1) 2 = 0<br />
g(0) = 7,<br />
g(1/2) = −1 + 3 − 3 + 7 = 6,<br />
g(1) = −8 + 12 − 6 + 7 = 5 ⇒ minimum.<br />
x2 (f,w)<br />
Ritzova metoda. Řešení ve tvaru u = aw, kde a ∈ R a w(x) = x − . Jest a =<br />
2 (Aw,w) .<br />
Počítejme (f = 3, w ′ = 1 − x)<br />
∫ 1<br />
) [<br />
(f,w) = 3<br />
(x − x2 1<br />
dx = 3<br />
0 2 2 x2 − 1 ] 1 ( 1<br />
6 x3 = 3<br />
0<br />
2 − 1 = 1,<br />
6)<br />
(Aw,w) =<br />
tedy a = 10<br />
19<br />
=<br />
=<br />
∫ 1 (<br />
−8x 3 + 12x 2 − 6x + 7 ) (1 − x) 2 dx − 3 ∫ 1<br />
) 2 (x − x2<br />
dx<br />
0<br />
2 0 2<br />
∫ 1<br />
(−8x 5 + 28x 4 − 38x 3 + 31x 2 − 20x + 7)dx − 3 ∫ 1<br />
(x 2 − x 3 + 1 )<br />
0<br />
2 0 4 x4 dx<br />
[<br />
− 8 6 x6 + 28 5 x5 − 38 4 x4 + 31<br />
1<br />
3 − 10x2 + 7x]<br />
− 3 [ 1<br />
0<br />
2 3 x3 − 1 4 x4 + 1 ] 1<br />
20 x5 0<br />
= − 4 3 + 28<br />
5 − 19<br />
= 6 +<br />
56 − 95<br />
10<br />
= 21<br />
10 − 2<br />
10 = 19<br />
10 ,<br />
2 + 31 3 − 10 + 7 − 3 ( 1<br />
2 3 − 1 4 + 1 )<br />
20<br />
− 3 ( 1<br />
2 12 + 1 )<br />
= 6 − 39<br />
20 10 − 3 8<br />
2 60 = 21<br />
10 − 4<br />
20<br />
a Ritzovo přibližné řešení je<br />
10<br />
19<br />
) (x − x2<br />
.<br />
2<br />
26 Využito ∫ b<br />
a u′2 dx ≥ 2<br />
(b−a) 2 ∫ b<br />
a u2 dx. Minimalizace použitá při odhadování integrálu je ukázána dále,<br />
minimum pro x = 1, hodnota koeficientu 5.<br />
55
Příklad 10.10: Operátorová rovnice Au = f i s nějakým lineárním operátorem A definovaným<br />
na D(A) = {v ∈ C 2 ([0,1]) : v(0) = 0 = v(1)} byla přibližně vyřešena Ritzovou metodou, a<br />
to pro tři různé pravé strany f i , i = 1,2,3. Přibližné řešení se hledalo ve tvaru u i = a i w, kde<br />
a i ∈ R a w = x(1 − x). Pro f 1 ≡ x 2 + sinπx bylo nalezeno přibližné řešení u 1 = π3 + 80<br />
40π 3 w,<br />
pro f 2 ≡ x 2 − sin πx bylo nalezeno přibližné řešení u 2 = π3 − 80<br />
40π 3 w, pro f 3 ≡ x bylo nalezeno<br />
přibližné řešení u 3 = 1 24 w. Stanovte konstantu a 4 ∈ R v přibližném řešení u 4 = a 4 x(1 − x),<br />
jestliže je dána pravá strana f 4 ≡ 1 + 4sin πx.<br />
Nápověda: Vyjděte z a i = (f i ,w)/(Aw,w), i = 1,2,3,4. Zamyslete se nad vztahem mezi f 4 a f i ,<br />
i = 1,2,3. Operátor A není zadán, hodnotu (Aw,w) však lze určit na základě zadaných veličin.<br />
Řešení: Povšimněme si, že f 4 = 2f 1 − 2f 2 + 1. Z a i = (f i,w)<br />
, i = 1,2,3,4, odvodíme<br />
(Aw,w)<br />
a 4 = (2f 1 − 2f 2 + 1,w)<br />
(Aw,w)<br />
= 2a 1 − 2a 2 + (1,w)<br />
(Aw,w) .<br />
Hodnotu (Aw,w) vypočítáme nejsnáze ze vztahu pro a 3 , a to takto<br />
Dále<br />
Celkem tedy<br />
a u 4 =<br />
(1,w) =<br />
(Aw,w) = 1 a 3<br />
(f 3 ,w) = 24<br />
∫ 1<br />
0<br />
a 4 = 2a 1 − 2a 2 +<br />
96 + π3<br />
12π 3 x(1 − x).<br />
∫ 1<br />
0<br />
x 2 (1 − x)dx = 24<br />
[ 1<br />
= 24<br />
3 x3 − 1 ] 1 [ 1<br />
4 x4 = 24<br />
0<br />
3 − 1 4]<br />
x(1 − x)dx =<br />
∫ 1<br />
0<br />
= 2.<br />
∫ 1<br />
0<br />
(x 2 − x 3 )dx<br />
[ 1<br />
(x − x 2 )dx =<br />
2 x2 − 1 ] 1 [ 1<br />
3 x3 =<br />
0<br />
2 − 1 =<br />
3]<br />
1 6 .<br />
1<br />
6<br />
2 = + 80<br />
2π3 40π 3 − 2 π3 − 80<br />
40π 3 + 1<br />
12 = 160<br />
20π 3 + 1 96 + π3<br />
=<br />
12 12π 3<br />
Příklad 10.11: Ritzovou metodou nalezněte přibližné řešení okrajové úlohy<br />
−(x 3 + 1)u ′′ − 3x 2 u ′ + x 3 u = x 4 , (18)<br />
u(1) = 2, u(3) = −4. (19)<br />
Při výpočtu přibližného řešení použijte podprostor generovaný bázovou funkcí<br />
w = (x − 1)(x − 3), kde x ∈ [1,3].<br />
Řešení: Úlohu upravíme tak, abychom získali okrajové podmínky s nulovými hodnotami. Toho<br />
se dosáhne tím, že řešení u hledáme ve tvaru u = û+φ, kde φ je dvakrát spojitě diferencovatelná<br />
funkce, pro niž platí, že φ(1) = 2 a φ(3) = −4. Pak totiž bude û(1) = 0 a û(3) = 0, což jsou<br />
okrajové podmínky, s nimiž již umíme počítat.<br />
Funkci φ volíme co nejjednodušší, postačí ve tvaru φ(x) = αx + β. Z podmínek<br />
φ(1) = 2 = α + β,<br />
φ(3) = −4 = 3α + β<br />
vypočteme α = −3 a β = 5, tedy φ(x) = −3x + 5.<br />
56
Upravíme rovnici (18) v původním nebo v divergentním tvaru dosazením u = û + φ.<br />
−(x 3 + 1)(û + φ) ′′ − 3x 2 (û + φ) ′ + x 3 (û + φ) = x 4 ,<br />
−(x 3 + 1)û ′′ − 3x 2 û ′ + x 3 û = x 4 + (x 3 + 1)φ ′′ + 3x 2 φ ′ − x 3 φ,<br />
−(x 3 + 1)û ′′ − 3x 2 û ′ + x 3 û = x 4 − 9x 2 − x 3 (−3x + 5),<br />
−(x 3 + 1)û ′′ − 3x 2 û ′ + x 3 û = 4x 4 − 5x 3 − 9x 2 .<br />
Řešení okrajové úlohy (18)-(19) tedy získáme prostřednictvím funkce φ a řešení úlohy<br />
−(x 3 + 1)û ′′ − 3x 2 û ′ + x 3 û = 4x 4 − 5x 3 − 9x 2 , (20)<br />
û(1) = 0, û(3) = 0. (21)<br />
Okrajovou úlohu (20)-(21) budeme řešit Ritzovou metodou. Přibližné řešení hledáme ve tvaru<br />
û 1 = aw, kde a ∈ R.<br />
Úloze (20)-(21) odpovídá operátor<br />
Aû ≡ − ( (x 3 + 1)û ′) ′<br />
+ x3û,<br />
kde û ∈ D(A) = { v ∈ C 2 ([1,3]) : v(1) = 0 = v(3) } . Snadno se ukáže, že operátor A je symetrický<br />
a pozitivně definitní na D(A), je tedy možné použít Ritzovu metodu.<br />
Platí, že a = (f,w)<br />
(Aw,w) , kde f = 4x4 − 5x 3 − 9x 2 .<br />
Jest<br />
(f,w) =<br />
(Aw,w) =<br />
∫ 3<br />
1<br />
∫ 3<br />
Přibližné řešení úlohy (18)-(19) tedy je<br />
1<br />
(<br />
4x 4 − 5x 3 − 9x 2) ( x 2 − 4x + 3 ) dx = 12<br />
35 ,<br />
( (x 3 + 1 ) (2x − 4) 2 + x 3 ( x 2 − 4x + 3 ) ) 2<br />
dx = 904<br />
21 .<br />
u 1 = û 1 + φ = aw + φ = 9 (x − 1)(x − 3) − 3x + 5.<br />
1130<br />
Příklad 10.12: Zadání je stejné jako v příkladu 10.3, jen přibližné řešení okrajové úlohy Ritzovou<br />
metodou se hledá ve tvaru<br />
w = c 1 v 1 + c 2 v 2 , kde v 1 = x(x − 1), v 2 = x 2 (x − 1) a c 1 ,c 2 ∈ R.<br />
Stačí, když pro výpočet neznámých hodnot c 1 a c 2 sestavíte rovnice s číselnými koeficienty.<br />
Řešení: První část řešení (symetrie, pozitivní definitnost) je shodná s příkladem 10.3, liší se<br />
výpočet přibližného řešení.<br />
Z podmínky minima funkcionálu energie<br />
F(u) = (Au,u) − 2(f,u) = (u,u) A − 2(f,u)<br />
plyne, že v Ritzově metodě jde o vyřešení problému (s využitím symetrie skalárního součinu<br />
(·, ·) A )<br />
min F(c 1v 1 + c 2 v 2 )<br />
c 1 ,c 2 ∈R<br />
(<br />
= min c<br />
2<br />
1 (v 1 ,v 1 ) A + 2c 1 c 2 (v 1 ,v 2 ) A + c 2 2 (v 2,v 2 ) A − 2c 1 (f,v 1 ) − 2c 2 (f,v 2 ) ) .<br />
c 1 ,c 2 ∈R<br />
57
Minima se nabývá v bodě, kde<br />
Odtud dostaneme obecný tvar soustavy<br />
∂F<br />
∂c 1<br />
= 0,<br />
∂F<br />
∂c 2<br />
= 0.<br />
Hodnoty<br />
(v 1 ,v 1 ) A c 1 + (v 1 ,v 2 ) A c 2 = (f,v 1 ),<br />
(v 1 ,v 2 ) A c 1 + (v 2 ,v 2 ) A c 2 = (f,v 2 ).<br />
(f,v 1 ) = − 1<br />
12 , (v 1,v 1 ) A = 1 3<br />
spočítáme jako v příkladu 10.3. Zbývá spočítat<br />
Dostáváme tedy soustavu<br />
(f,v 2 ) =<br />
(v 1 ,v 2 ) A =<br />
(v 2 ,v 2 ) A =<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
x 3 (x − 1)dx = − 1<br />
20 ,<br />
( ) 1 (x<br />
2 + x 2 − x ) ′ (<br />
x 3 − x 2) ′ 1 dx =<br />
5 ,<br />
( ) 1 (x<br />
2 + x 3 − x 2) ′ (<br />
x 3 − x 2) ′ 1 dx =<br />
6 .<br />
1<br />
3 c 1 + 1 5 c 2 = − 1 12 ,<br />
1<br />
5 c 1 + 1 6 c 2 = − 1 20 .<br />
Poznámka: Další řešené příklady na použití Ritzovy metody najdete v [2, oddíly 86 a 89].<br />
11 Pozitivní definitnost operátorů,<br />
metoda sítí<br />
Doporučuji přečíst si text na začátku kapitoly 9 a věnovat pozornost i obtížnějším příkladům<br />
9.8 a 9.9.<br />
Příklad 11.1: K okrajové úloze<br />
(<br />
x 2 − 2x + 3 ) u ′′ + (2x − 2)u ′ = x 2 − 5,<br />
u(0) = 0, u(4) = 0,<br />
najděte operátor A symetrický na svém definičního oboru D(A) a takový, aby pro každou funkci<br />
v ∈ D(A) platilo (Av,v) ≥ c‖v‖ 2 L 2 (0,4), kde c je kladná konstanta, tuto konstantu konkretizujte.<br />
Napište operátorovou rovnici.<br />
Metodou sítí s krokem h = 1 pak najděte přibližné řešení okrajové úlohy v bodech x 1 = 1,<br />
x 2 = 2 a x 3 = 3. (Pro aproximaci první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈<br />
(U i+1 − U i−1 )/(2h).)<br />
Řešení: Levou stranu rovnice napíšeme v divergentním tvaru ( (x 2 − 2x + 3)u ′) ′ , abychom dostali<br />
pozitivní operátor, musíme ještě změnit znaménko (vynásobit rovnici číslem −1).<br />
58
Hledaný operátor Au ≡ − ( (x 2 − 2x + 3)u ′) ′ , jeho definiční obor<br />
D(A) = {u ∈ C 2 ([0,4]) : u(0) = 0 = u(4)}. Operátorová rovnice: najít funkci u ∈ D(A) takovou,<br />
aby platilo Au = 5 − x 2 (změna znaménka pravé strany).<br />
Symetrie (zdůvodnění!).<br />
Pozitivní definitnost (ve smyslu skript [2]; použita Friedrichsova nerovnost (12)), například<br />
c = 1/4.<br />
K odvození rovnic metodou sítí použijeme původní tvar diferenciální rovnice (tvar divergentní<br />
je nevhodný).<br />
Označme U i = ih přibližné řešení v bodě x i = 0+ih, kde i = 0,1,2,3,4 a h = 1; jest U 0 = 0<br />
a U 4 = 0.<br />
Diferenční rovnice pro x 1 = 1:<br />
Diferenční rovnice pro x 2 = 2:<br />
Diferenční rovnice pro x 3 = 3:<br />
2 U 0 − 2U 1 + U 2<br />
+ 0 = −4,<br />
1<br />
−4U 1 + 2U 2 = −4.<br />
3 U 1 − 2U 2 + U 3<br />
+ 2 U 3 − U 1<br />
= −1,<br />
1 2<br />
2U 1 − 6U 2 + 4U 3 = −1.<br />
6 U 2 − 2U 3 + U 4<br />
1<br />
+ 4 U 4 − U 2<br />
= 4,<br />
2<br />
4U 2 − 12U 3 = 4.<br />
Maticově<br />
⎛<br />
−4 2 0 |<br />
⎞<br />
−4<br />
⎛<br />
−2 1 0 |<br />
⎞<br />
−2<br />
⎝ 2 −6 4 | −1⎠ ∼ ⎝ 2 −6 4 | −1⎠<br />
0 4 −12 | 4 0 1 −3 | 1<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
−2 1 0 | −2 −2 1 0 | −2<br />
∼ ⎝ 0 −5 4 | −3⎠ ∼ ⎝ 0 −5 4 | −3⎠ .<br />
0 1 −3 | 1 0 0 −11 | 2<br />
Odtud<br />
U 3 = − 2 11 ,<br />
(<br />
−5U 2 = −3 − 4 − 2 )<br />
( 5<br />
−2U 1 = −2 −<br />
11)<br />
= −33 + 8<br />
11<br />
= −27<br />
11 ⇒ U 1 = 27<br />
22 .<br />
= −25<br />
11 ⇒ U 2 = 5<br />
11 ,<br />
Příklad 11.2: Stanovte operátor (včetně definičního oboru D(A)) príslušný okrajové úloze<br />
( ) 1<br />
−<br />
4 + x2 u ′′ − 2xu ′ = − 60<br />
2 + x ,<br />
u(−1) = 0, u(1) = 0.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (−1,1), kde c je kladná konstanta, tuto konstantu konkretizujte. Metodou sítí s krokem<br />
59
h = 1/2 pak najděte přibližné řešení okrajové úlohy v bodech x 1 = −1/2, x 2 = 0 a x 3 = 1/2.<br />
(Pro aproximaci první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈ (U i+1 − U i−1 )/(2h).)<br />
Řešení: Operátor Au ≡ − ( (1/4 + x 2 )u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([−1,1]) : u(−1) = 0 = u(1)}.<br />
Symetrie (zdůvodnění!). Pozitivní definitnost (ve smyslu skript [2]), 27 c = 1/8.<br />
Označme U i = ih přibližné řešení v bodě x i = −1 + ih, kde i = 0,1,2,3,4 a h = 1/2; jest<br />
U 0 = 0 a U 4 = 0. Pro zjednodušení násobme −1: (1/4 + x 2 )u ′′ + 2xu ′ = 60/(2 + x).<br />
Sít’ová rovnice pro x 1 = −1/2:<br />
Sít’ová rovnice pro x 2 = 0:<br />
Sít’ová rovnice pro x 3 = 1/2:<br />
2 U 0 − 2U 1 + U 2<br />
4<br />
1<br />
+ 2 −1<br />
2 (U 2 − U 0 ) = 60 2 3 ,<br />
4<br />
−4U 1 + U 2 = 40.<br />
1 U 1 − 2U 2 + U 3<br />
4<br />
1<br />
+ 0 = 60 1 2 ,<br />
4<br />
U 1 − 2U 2 + U 3 = 30.<br />
2 U 2 − 2U 3 + U 4<br />
4<br />
1<br />
+ 2 1 2 (U 4 − U 2 ) = 60 2 5 ,<br />
4<br />
U 2 − 4U 3 = 24.<br />
⎛<br />
⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
−4 1 0 | 40 1 −2 1 | 30 1 −2 1 | 30<br />
⎝ 1 −2 1 | 30⎠ ∼ ⎝−4 1 0 | 40⎠ ∼ ⎝0 −7 4 | 160⎠<br />
0 1 −4 | 24 0 1 −4 | 24 0 1 −4 | 24<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 −2 1 | 30 1 −2 1 | 30<br />
∼ ⎝0 1 −4 | 24 ⎠ ∼ ⎝0 1 −4 | 24 ⎠.<br />
0 −7 4 | 160 0 0 −24 | 328<br />
Odtud<br />
U 3 = − 328<br />
24 = −41 3 ,<br />
U 2 = 24 + 4U 3 = 72 3 − 164<br />
3 = −92 3 ,<br />
U 1 = 30 − U 3 + 2U 2 = 90<br />
3 + 41 3 − 184<br />
3 = −53 3 .<br />
Příklad 11.3: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
− ( 1 + x + x 2) u ′′ − (2x + 1)u ′ = −6 − 2x,<br />
u(−1) = 0, u(1) = 0.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (−1,1), kde c je kladná konstanta, tuto konstantu konkretizujte. Metodou sítí s krokem<br />
27 Studenti by měli znát Friedrichsovu nerovnost v 1D: ∫ b<br />
a v′2 dx ≥<br />
60<br />
2<br />
(b − a) 2 ∫ b<br />
a v2 dx, pokud v(a) = 0.
h = 1/2 pak najděte přibližné řešení okrajové úlohy v bodech x 1 = −1/2, x 2 = 0 a x 3 = 1/2.<br />
(Pro aproximaci první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈ (U i+1 − U i−1 )/(2h).)<br />
Řešení: Operátor Au ≡ − ( (1 + x + x 2 )u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([−1,1]) : u(−1) = 0 = u(1)}.<br />
Symetrie (zdůvodnění!). Pozitivní definitnost (ve smyslu skript [2]), c = 3/8. 28<br />
Označme U i = ih přibližné řešení v bodě x i = −1 + ih, kde i = 0,1,2,3,4 a h = 1/2; jest<br />
U 0 = 0 a U 4 = 0. Pro zjednodušení násobme −1: (1 + x + x 2 )u ′′ + (2x + 1)u ′ = 6 + 2x.<br />
Sít’ová rovnice pro x 1 = −1/2:<br />
Sít’ová rovnice pro x 2 = 0:<br />
Sít’ová rovnice pro x 3 = 1/2:<br />
−6U 1 + 3U 2 = 5.<br />
3U 1 − 8U 2 + 5U 3 = 6.<br />
5U 2 − 14U 3 = 7.<br />
Maticově<br />
⎛<br />
−6 3 0 |<br />
⎞<br />
5<br />
⎛<br />
−6 3 0 |<br />
⎞<br />
5<br />
⎛<br />
−6 3 0 |<br />
⎞<br />
5<br />
⎝ 3 −8 5 | 6⎠ ∼ ⎝ 0 −13 10 | 17⎠ ∼ ⎝ 0 −13 10 | 17 ⎠ .<br />
0 5 −14 | 7 0 5 −14 | 7 0 0 −132 | 176<br />
Odtud<br />
U 3 = − 176<br />
132 = −44 33 = −4 3 ,<br />
(<br />
−13U 2 = 17 − 10 − 4 )<br />
51 + 40<br />
= = 91<br />
3 3 3 ⇒ U 2 = − 7 3 ,<br />
(<br />
−6U 1 = 5 − 3 − 7 )<br />
= 5 + 7 = 12 ⇒ U 1 = −2.<br />
3<br />
Příklad 11.4: Stanovte operátor A (včetně definičního oboru D(A)) příslušný okrajové úloze<br />
− ( x 2 − 2x + 3 ) u ′′ − (2x − 2)u ′ = 5 − x 2 ,<br />
u(0) = 0, u(4) = 0.<br />
Ukažte, že operátor je symetrický na D(A) a že pro každou funkci v ∈ D(A) platí (Av,v) ≥<br />
c‖v‖ 2 L 2 (0,4), kde c je kladná konstanta, tuto konstantu konkretizujte. Metodou sítí s krokem h = 1<br />
pak najděte přibližné řešení okrajové úlohy v bodech x 1 = 1, x 2 = 2 a x 3 = 3. (Pro aproximaci<br />
první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈ (U i+1 − U i−1 )/(2h).)<br />
Řešení: Operátor Au ≡ − ( (x 2 − 2x + 3)u ′) ′ s definičním oborem<br />
D(A) = {u ∈ C 2 ([0,4]) : u(0) = 0 = u(4)}.<br />
Symetrie (zdůvodnění!). Pozitivní definitnost (ve smyslu skript [2]), 29 c = 1/4.<br />
28 Studenti by měli umět najít minimum funkce 1 + x+x 2 na intervalu [−1, 1] (nabývá se v x = −1/2)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b 2 ∫ b<br />
a v′2 dx ≥<br />
(b − a) 2 a v2 dx, pokud v(a) = 0.<br />
29 Studenti by měli umět najít minimum funkce x 2 − 2x + 3 na intervalu [0, 4] (nabývá se v x = 1)<br />
a znát Friedrichsovu nerovnost v 1D: ∫ b<br />
a v′2 dx ≥<br />
2<br />
(b − a) 2 ∫ b<br />
a v2 dx, pokud v(a) = 0.<br />
61
Označme U i = ih přibližné řešení v bodě x i = 0+ih, kde i = 0,1,2,3,4 a h = 1; jest U 0 = 0<br />
a U 4 = 0. Pro zjednodušení násobme −1: ( x 2 − 2x + 3 ) u ′′ + (2x − 2)u ′ = x 2 − 5.<br />
Sít’ová rovnice pro x 1 = 1:<br />
Sít’ová rovnice pro x 2 = 2:<br />
Sít’ová rovnice pro x 3 = 3:<br />
Odtud<br />
U 3 = − 2 11 ,<br />
(<br />
−5U 2 = −3 − 4 − 2 )<br />
( 5<br />
−2U 1 = −2 −<br />
11)<br />
−4U 1 + 2U 2 = −4.<br />
2U 1 − 6U 2 + 4U 3 = −1.<br />
4U 2 − 12U 3 = 4.<br />
= −33 + 8<br />
11<br />
= −27<br />
11 ⇒ U 1 = 27<br />
22 .<br />
= −25<br />
11 ⇒ U 2 = 5<br />
11 ,<br />
12 Metoda sítí v 1D: okrajové úlohy<br />
Příklad 12.1: Metodou sítí s krokem h = 1/2 najděte přibližné řešení okrajové úlohy<br />
( ) 1<br />
−<br />
4 + x2 u ′′ − 2xu ′ = − 60<br />
2 + x ,<br />
u(−1) = 0, u(1) = 0.<br />
v bodech x 1 = −1/2, x 2 = 0 a x 3 = 1/2. (Pro aproximaci první derivace použijte symetrické<br />
schéma, tj. u ′ (x i ) ≈ (U i+1 − U i−1 )/(2h).)<br />
Řešení: Označme U i = ih přibližné řešení v bodě x i = −1 + ih, kde i = 0,1,2,3,4 a h = 1/2;<br />
jest U 0 = 0 a U 4 = 0. Pro zjednodušení rovnici násobme −1 (při sestavování diferenčních rovnic<br />
se lépe pracuje s výrazy, před nimiž nestojí znaménko mínus, neudělá se tolik chyb):<br />
Diferenční rovnice pro x 1 = −1/2:<br />
Diferenční rovnice pro x 2 = 0:<br />
(1/4 + x 2 )u ′′ + 2xu ′ = 60/(2 + x).<br />
2 U 0 − 2U 1 + U 2<br />
4<br />
1<br />
+ 2 −1<br />
2 (U 2 − U 0 ) = 60 2 3 ,<br />
4<br />
−4U 1 + U 2 = 40.<br />
1 U 1 − 2U 2 + U 3<br />
4<br />
1<br />
+ 0 = 60 1 2 ,<br />
4<br />
U 1 − 2U 2 + U 3 = 30.<br />
62
Diferenční rovnice pro x 3 = 1/2:<br />
2 U 2 − 2U 3 + U 4<br />
4<br />
1<br />
+ 2 1 2 (U 4 − U 2 ) = 60 2 5 ,<br />
4<br />
U 2 − 4U 3 = 24.<br />
Maticově<br />
⎛ ⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
−4 1 0 | 40 1 −2 1 | 30 1 −2 1 | 30<br />
⎝ 1 −2 1 | 30⎠ ∼ ⎝−4 1 0 | 40⎠ ∼ ⎝0 −7 4 | 160⎠<br />
0 1 −4 | 24 0 1 −4 | 24 0 1 −4 | 24<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 −2 1 | 30 1 −2 1 | 30<br />
∼ ⎝0 1 −4 | 24 ⎠ ∼ ⎝0 1 −4 | 24 ⎠.<br />
0 −7 4 | 160 0 0 −24 | 328<br />
Odtud<br />
U 3 = − 328<br />
24 = −41 3 ,<br />
U 2 = 24 + 4U 3 = 72 3 − 164<br />
3 = −92 3 ,<br />
U 1 = 30 − U 3 + 2U 2 = 90<br />
3 + 41 3 − 184<br />
3 = −53 3 .<br />
Příklad 12.2: Řešte problém u ′′<br />
− (1 + 2x)u = 2x,<br />
4<br />
u(0) = 0, u(2) = 0<br />
približně metodou sítí s délkou kroku 1/2.<br />
Řešení: Označme U i = ih přibližné řešení v bodě x i = ih, kde i = 0,1,2,3,4; jest U 0 = U 4 = 0.<br />
Sít’ová rovnice pro x 1 = 1 2 : 1 0 − 2U 1 + U 2<br />
4<br />
1<br />
− (1 + 1)U 1 = 1,<br />
4<br />
−4U 1 + U 2 = 1.<br />
Sít’ová rovnice pro x 2 = 1:<br />
Sít’ová rovnice pro x 3 = 3/2:<br />
1 U 1 − 2U 2 + U 3<br />
4<br />
1<br />
− (1 + 2)U 2 = 2,<br />
4<br />
U 1 − 5U 2 + U 3 = 2.<br />
1 U 2 − 2U 3 + 0<br />
4<br />
1<br />
− (1 + 3)U 3 = 3,<br />
4<br />
U 2 − 6U 3 = 3.<br />
Maticově<br />
⎛<br />
−4 1 0 |<br />
⎞<br />
1<br />
⎛<br />
−4 1 0 |<br />
⎞<br />
1<br />
⎛<br />
−4 1 0 |<br />
⎞<br />
1<br />
⎝ 1 −5 1 | 2⎠ ∼ ⎝ 0 −19 4 | 9⎠ ∼ ⎝ 0 −19 4 | 9 ⎠.<br />
0 1 −6 | 3 0 1 −6 | 3 0 0 −110 | 66<br />
63
Řešení (−2/5, −3/5, −3/5) T .<br />
Příklad 12.3:<br />
Řešte problém<br />
u ′′<br />
4<br />
− (1 + 2x)u = 2x, u(0) = 0, u(2) = 0,<br />
přibližně metodou sítí s délkou kroku 1/2.<br />
Řešení: Označme U i přibližné řešení v bodě x i = ih, kde i = 0,1,2,3,4; jest U 0 = U 4 = 0.<br />
Sít’ová rovnice pro x 1 = 1 2 : −4U 1 + U 2 = 1.<br />
Sít’ová rovnice pro x 2 = 1:<br />
U 1 − 5U 2 + U 3 = 2.<br />
Sít’ová rovnice pro x 3 = 3/2:<br />
U 2 − 6U 3 = 3.<br />
Řešení (−2/5, −3/5, −3/5) T .<br />
Příklad 12.4: Problém<br />
( 1<br />
2 + x )<br />
u ′′ (x) − 4xu(x) = 4x,<br />
u(0) = 1, u(2) = −1<br />
řešte metodou sítí s délkou kroku 1/2 a vypočtěte hodnotu přibližného řešení v bodě x = 3/2.<br />
Řešení: Označme U i = ih přibližné řešení v bodě x i = ih, kde i = 0,1,2,3,4 a h = 1/2; jest<br />
U 0 = 1 a U 4 = −1.<br />
Sít’ová rovnice pro x 1 = 1 2 : −5U 1 + 2U 2 = −1.<br />
Sít’ová rovnice pro x 2 = 1:<br />
Sít’ová rovnice pro x 3 = 3/2:<br />
Odtud U 3 = − 133<br />
157 .<br />
Příklad 12.5: Problém<br />
3U 1 − 8U 2 + 3U 3 = 2.<br />
4U 2 − 11U 3 = 7.<br />
(<br />
x 2 − 2x + 2 ) u ′′ (x) + 4x 2 u(x) = cos(πx),<br />
u(0) = 2, u(2) = 1<br />
řešte metodou sítí s délkou kroku 1/2 a vypočtěte hodnotu přibližného řešení v bodě x = 3/2.<br />
64
Řešení: Označme U i = ih přibližné řešení v bodě x i = ih, kde i = 0,1,2,3,4 a h = 1/2; jest<br />
U 0 = 2 a U 4 = 1.<br />
Sít’ová rovnice pro x 1 = 1 2 : −9U 1 + 5U 2 = −10.<br />
Sít’ová rovnice pro x 2 = 1:<br />
Sít’ová rovnice pro x 3 = 3/2:<br />
Odtud U 3 = − 325<br />
164 .<br />
4U 1 − 4U 2 + 4U 3 = −1.<br />
5U 2 − U 3 = −5.<br />
Příklad 12.6: Metodou sítí s krokem h = π/4 najděte přibližné řešení okrajové úlohy<br />
π 2<br />
4 (1 + sin2 x)u ′′ + 2xu ′ − 2u = −2cos 2 x,<br />
u(0) = 1, u(π) = −1<br />
v bodě x = 3π/4. Pro aproximaci první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈ (U i+1 −<br />
U i−1 )/(2h). (Poznámka: sin(π/4) = √ 2/2.)<br />
Řešení: U i značí přibližné řešení v bodě x i = ih, kde i = 1,2,3; dále U 0 = 1, U 4 = −1. Sít’ová<br />
rovnice pro x 1 = π/4:<br />
π 2 (<br />
1 + 1 ) 1 − 2U1 + U 2<br />
+ 2 π U 2 − 1<br />
4 2 π 2<br />
4 2 π − 2U 1 = −1,<br />
16<br />
4<br />
Sít’ová rovnice pro x 2 = π/2:<br />
4 3 2 (1 − 2U 1 + U 2 ) + U 2 − 1 − 2U 1 = −1,<br />
6 − 12U 1 + 6U 2 + U 2 − 2U 1 = 0,<br />
−14U 1 + 7U 2 = −6.<br />
π 2<br />
4 (1 + 1) U 1 − 2U 2 + U 3<br />
+ 2 π U 3 − U 1<br />
π 2<br />
2 2 π − 2U 2 = 0,<br />
16<br />
4<br />
8(U 1 − 2U 2 + U 3 ) + 2U 3 − 2U 1 − 2U 2 = 0,<br />
Sít’ová rovnice pro x 3 = 3π/4:<br />
π 2 (<br />
1 + 1 )<br />
U2 − 2U 3 − 1<br />
+ 2 3π 4 2<br />
4<br />
π 2<br />
16<br />
6U 1 − 18U 2 + 10U 3 = 0,<br />
3U 1 − 9U 2 + 5U 3 = 0.<br />
−1 − U 2<br />
2 π 4<br />
− 2U 3 = −1,<br />
4 3 2 (U 2 − 2U 3 − 1) + 3(−1 − U 2 ) − 2U 3 = −1,<br />
6U 2 − 12U 3 − 6 − 3 − 3U 2 − 2U 3 = −1,<br />
3U 2 − 14U 3 = 8.<br />
65
Maticově<br />
⎛<br />
⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
−14 7 0 | −6 −14 7 0 | −6 −14 7 0 | −6<br />
⎝ 3 −9 5 | 0 ⎠ ∼ ⎝ 0 −105 70 | −18⎠ ∼ ⎝ 0 −105 70 | −18⎠<br />
0 3 −14 | 8 0 3 −14 | 8 0 105 −490 | 280<br />
⎛<br />
⎞<br />
−14 7 0 | −6<br />
∼ ⎝ 0 −105 70 | −18⎠.<br />
0 0 −420 | 262<br />
Odtud U 3 = − 262<br />
420 = −131 210 .<br />
Příklad 12.7: Uplatněte metodou sítí s krokem h = 1/2 na okrajovou úlohu<br />
(5 − 2x)u ′′ − 2u ′ − 8x 2 u = 38 − 8x 2 ,<br />
u(0) = 2, u(2) = 1.<br />
Sestavte příslušnou soustavu lineárních algebraických rovnic a zapište ji v maticovém tvaru.<br />
Rovnice však neřešte. Pro aproximaci první derivace použijte symetrické schéma, tj. u ′ (x i ) ≈<br />
(U i+1 − U i−1 )/(2h).<br />
Řešení: U i značí přibližné řešení v bodě x i = ih, kde i = 1,2,3; dále U 0 = 2, U 4 = 1. Sít’ová<br />
rovnice pro x 1 = 1/2:<br />
Sít’ová rovnice pro x 2 = 1:<br />
Sít’ová rovnice pro x 3 = 3/2:<br />
34U 1 − 14U 2 = 0.<br />
14U 1 − 32U 2 + 10U 3 = 30.<br />
10U 2 − 34U 3 = 14.<br />
Maticově<br />
⎛<br />
17 −7 0 |<br />
⎞<br />
0<br />
⎝ 7 −16 5 | 15⎠<br />
0 5 −17 | 7<br />
Příklad 12.8: Řešte problém u ′′ − (1 + sin 2 x)u = −4,<br />
u(0) = 0, u(π) = 0<br />
přibližně metodou sítí s délkou kroku h = π/3.<br />
Řešení: Podrobné řešení viz [2, oddíl 25].<br />
13 Metoda sítí v 1D: vlastní čísla okrajových úloh<br />
Příklad 13.1: Metodou sítí najděte přibližně první dvě vlastní čísla problému<br />
u ′′ + λ4 x u = 0,<br />
u(0) = 0, u(3/2) = 0.<br />
66
Interval rozdělte rovnoměrně na tři podintervaly.<br />
Řešení: Vnitřní body dělení jsou x 1 = 1/2 a x 2 = 1, krok dělení h = 1/2. Hodnoty u(x 1 ) a<br />
u(x 2 ) budeme aproximovat (prozatím neznámými) hodnotami U 1 a U 2 . Vlastní číslo budeme<br />
aproximovat (prozatím neznámou) hodnotou µ.<br />
Diferenční rovnice (s využitím okrajových podmínek)<br />
upravíme například takto<br />
−2U 1 + U 2<br />
1<br />
4<br />
U 1 − 2U 2<br />
1<br />
4<br />
+ µ4 1 2 U1 = 0,<br />
+ µ4 1 U 2 = 0<br />
(µ − 4)U 1 + 2U 2 = 0, (22)<br />
U 1 + (µ − 2)U 2 = 0. (23)<br />
Tato soustava má nenulové řešení přávě tehdy, když determinant její matice je roven nule. Odtud<br />
dostáváme kvadratickou rovnici pro µ<br />
(µ − 4)(µ − 2) − 2 = 0,<br />
z níž plyne µ 1 = 3 − √ 3 ≈ 1,27 a µ 2 = 3 + √ 3 ≈ 4,73.<br />
Soustavu (22)-(23) můžeme zapsat i takto<br />
4U 1 − 2U 2 = µU 1 ,<br />
−U 1 + 2U 2 = µU 2 ,<br />
z níž je patrné, že je zapotřebí najít vlastní čísla matice<br />
( ) 4 −2<br />
A = ,<br />
−1 2<br />
ta ovšem jsou µ 1 = 3 − √ 3 a µ 2 = 3 + √ 3.<br />
Příklad 13.2: Metodou sítí najděte přibližně první dvě vlastní čísla problému<br />
u ′′ + λ 24(1 + x − x2 )<br />
u = 0,<br />
1 + x<br />
u(0) = 0, u(3/2) = 0.<br />
Interval rozdělte rovnoměrně na tři podintervaly.<br />
Řešení: Vnitřní body dělení jsou x 1 = 1/2 a x 2 = 1, krok dělení h = 1/2. Hodnoty u(x 1 ) a u(x 2 )<br />
budeme aproximovat hodnotami U 1 a U 2 . Vlastní číslo budeme aproximovat hodnotou µ.<br />
Diferenční rovnice (s využitím okrajových podmínek)<br />
−2U 1 + U 2<br />
1<br />
4<br />
+ µ 24(1 + 1 2 − 1 4 )<br />
1 + 1 U 1 = 0,<br />
2<br />
U 1 − 2U 2<br />
1<br />
4<br />
−8U 1 + 4U 2 + µ 24 5 4<br />
3<br />
U 1 = 0,<br />
2<br />
−8U 1 + 4U 2 + 20µU 1 = 0; (24)<br />
+ µ<br />
24(1 + 1 − 1)<br />
U 2 = 0,<br />
1 + 1<br />
4U 1 − 8U 2 + µ12U 2 = 0 (25)<br />
67
po úpravě (24), (25) krácením dostaneme soustavu<br />
(5µ − 2)U 1 + U 2 = 0,<br />
U 1 + (3µ − 2)U 2 = 0,<br />
která má nenulové řešení právě tehdy, když<br />
0 = (5µ − 2)(3µ − 2) − 1 = 15µ 2 − 16µ + 3.<br />
Řešením jsou hodnoty<br />
µ 1,2 = 16 ± √ 16 2 − 4 · 15 · 3<br />
30<br />
jež zároveň aproximují první dvě vlastní čísla úlohy. 30<br />
= 16 ± √ 4 · 19<br />
30<br />
= 8 ± √ 19<br />
,<br />
15<br />
Příklad 13.3: Metodou sítí najděte přibližně první dvě vlastní čísla problému<br />
u ′′ + λ 2 + x<br />
1 − x u = 0,<br />
u(−1) = 0, u(1/2) = 0.<br />
Interval rozdělte rovnoměrně na tři podintervaly.<br />
Řešení: Vnitřní body dělení jsou x 1 = −1/2 a x 2 = 0, krok dělení h = 1/2. Hodnoty u(x 1 ) a<br />
u(x 2 ) budeme aproximovat hodnotami U 1 a U 2 . Vlastní číslo budeme aproximovat hodnotou µ.<br />
Diferenční rovnice (s využitím okrajových podmínek)<br />
Po úpravě (26), (27) tvoří soustavu<br />
která má nenulové řešení právě tehdy, když<br />
Řešením jsou hodnoty<br />
3<br />
−2U 1 + U 2 2<br />
1<br />
+ µ<br />
3<br />
U 1 = 0,<br />
4 2<br />
−8U 1 + 4U 2 + µU 1 = 0; (26)<br />
U 1 − 2U 2<br />
1<br />
+ µ2U 2 = 0,<br />
4<br />
4U 1 − 8U 2 + µ2U 2 = 0. (27)<br />
(µ − 8)U 1 + 4U 2 = 0,<br />
4U 1 + (2µ − 8)U 2 = 0,<br />
0 = (µ − 8)(2µ − 8) − 16 = 2[(µ − 8)(µ − 4) − 8] = 2 [ µ 2 − 12µ + 24 ] .<br />
µ 1,2 = 12 ± √ 12 2 − 4 · 24<br />
2<br />
= 12 ± √ 4 · 12<br />
2<br />
jež zároveň aproximují první dvě vlastní čísla úlohy.<br />
= 6 ± √ 12 = 6 ± 2 √ 3,<br />
Poznámka: Další řešený příklad na vlastní čísla naleznete v [2, strana 27].<br />
( 30 K témuž ) výsledku bychom dospěli i druhou cestou — nalezením vlastních čísel matice<br />
2/5 −1/5<br />
, viz řešení Příkladu 13.1.<br />
−1/3 2/3<br />
68
14 Metoda sítí ve 2D: Liebmannova iterace<br />
Příklad 14.1: Necht’ Γ značí hranici čtverce Ω = (0,3) × (0,3). Liebmannovou iterací řešte<br />
problém<br />
−∆u = 0 v Ω,<br />
u = (x − y) 2 − 2y 2 na Γ.<br />
Sít’ zvolte s krokem 1. Neznámé hodnoty<br />
přibližného řešení ve vnitřních uzlech označte dle<br />
obrázku. Jako počáteční aproximaci zvolte nulové<br />
hodnoty ve vnitřních uzlech. Proved’te tři iterační<br />
cykly, v každém cyklu vyčíslujte v pořadí u 1 , u 2 ,<br />
u 3 , u 4 . Výsledky zaokrouhlujte na dvě platné cifry.<br />
Řešení:<br />
Z okrajové podmínky určíme hodnoty v uzlech na hranici<br />
čtverce (viz obrázek).<br />
Výchozí hodnoty u 1 = u 2 = u 3 = u 4 = 0.<br />
1. iterace:<br />
u 1 = −14−4<br />
4<br />
= −4,5,<br />
u 2 = −4,5−17−7<br />
4<br />
≈ −7,1,<br />
u 3 = −7,1+2+4<br />
4<br />
≈ −0,3,<br />
u 4 = −0,3−1+1−4,5<br />
4<br />
≈ −1,2.<br />
2. iterace:<br />
u 1 = −1,2−4−14−7,1<br />
4<br />
≈ −6,6,<br />
u 2 = −6,6−17−7−0,3<br />
4<br />
≈ −7,7,<br />
u 3 = −7,7+2+4−1,2<br />
4<br />
≈ −0,7,<br />
u 4 = −0,7+1−1−6,6<br />
4<br />
≈ −1,8.<br />
−9<br />
−4<br />
−1<br />
u 1<br />
u 2<br />
u 4 u 3<br />
−14<br />
u 1<br />
−17<br />
u 2<br />
u 4 u 3<br />
0 1 4 9<br />
3. iterace:<br />
u 1 = −1,8−4−14−7,7<br />
4<br />
≈ −6,9,<br />
u 2 = −6,9−17−7−0,7<br />
4<br />
≈ −7,9,<br />
u 3 = −7,9+2+4−1,8<br />
4<br />
≈ −0,9,<br />
u 4 = −0,9+1−1−6,6<br />
4<br />
≈ −1,9.<br />
Příklad 14.2: Necht’ Γ značí hranici čtverce Ω = (−1,2) × (−1,2). Liebmannovou iterací řešte<br />
problém<br />
∆u = 0 v Ω,<br />
u = x 3 + (x − 1) 2 − sin(πy/2) na Γ.<br />
−18<br />
−7<br />
2<br />
Sít’ zvolte s krokem 1. Neznámé hodnoty přibližného řešení ve<br />
vnitřních uzlech označte dle obrázku. Jako počáteční aproximaci<br />
zvolte u (0)<br />
1 = u (0)<br />
2 = u (0)<br />
3 = u (0)<br />
4 = 1. Postupujte<br />
v pořadí u (0)<br />
1 , u(0) 2 , u(0) 3 , u(0)<br />
tj. spočtěte u (i)<br />
1 = u (i)<br />
2 = u (i)<br />
na dvě platné cifry.<br />
Řešení:<br />
4 a proved’te dva iterační cykly,<br />
3 = u (i)<br />
4 , i = 1,2. Zaokrouhlujte<br />
u 1<br />
u 2<br />
u 4 u 3<br />
69
3<br />
1 1<br />
9<br />
2<br />
3<br />
u 1 u 2 8 Hodnoty v uzlech na Γ.<br />
Počáteční iterace: u 1 = u 2 = u 3 = u 4 = 1.<br />
u 4 u 3 9<br />
1. iterace: u 1 = 1,3, u 2 = 2,8, u 3 = 3,7, u 4 = 2,5.<br />
2. iterace: u 1 = 2,1, u 2 = 3,7, u 3 = 4,3, u 4 = 2,9.<br />
4 2 2 10<br />
15 Metoda sítí ve 2D: Dirichletova úloha<br />
Příklad 15.1: Na obdélníku Ω = (0, 2) × (0, 1) s hranicí Γ řešte metodou sítí problém<br />
−∆u = −48x v Ω,<br />
u = 2x + 6y + 1 na Γ.<br />
V obou směrech volte diskretizační krok h = 1/2. (Pozor: Obecná diferenční rovnice se někdy<br />
uvádí pro operátor −∆, jindy pro ∆; při výpočtech vyjděte ze správné varianty.)<br />
Řešení:<br />
Z okrajové podmínky vypočteme hodnoty v uzlech<br />
sítě ležících na hranici Γ. Neznámé hodnoty<br />
přibližného řešení ve vnitřních uzlech označíme<br />
u 1 , u 2 a u 3 .<br />
1 2 3 4 5<br />
Diferenční rovnice v uzlu (x i ,y j ) (pětibodové schéma) pro operátor −∆:<br />
7<br />
4<br />
8<br />
9<br />
10<br />
u 1 u 2 u 3<br />
11<br />
8<br />
− Uj i+1 − 2Uj i + Uj i−1<br />
h 2<br />
− Uj+1 i<br />
− 2U j i + Uj−1 i<br />
q 2 = f j i .<br />
Jestliže h = q, což je náš případ, pak<br />
−U j i+1 − Uj i−1 − Uj+1 i<br />
− U j−1<br />
i<br />
+ 4U j i = h2 f j i . (28)<br />
Vyčíslíme h 2 f j i<br />
ve vnitřních uzlech sítě a spolu s již známými hodnotami v uzlech na hranici<br />
obdélníka dosadíme do (28). V našem značení (viz obrázek sítě) dostaneme tuto soustavu rovnic<br />
4u 1 − u 2 − 2 − 4 − 8 = −6,<br />
−u 1 + 4u 2 − u 3 − 3 − 9 = −12,<br />
−u 2 + 4u 3 − 4 − 8 − 10 = −18.<br />
Maticově<br />
⎛<br />
⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
4 −1 0 | 8 4 −1 0 | 8 4 −1 0 | 8<br />
⎝−1 4 −1 | 0⎠ ∼ ⎝0 15 −4 | 8⎠ ∼ ⎝0 15 −4 | 8 ⎠ ,<br />
0 −1 4 | 4 0 −1 4 | 4 0 0 56 | 68<br />
70
řešení (u 1 , u 2 , u 3 ) T = (31/14, 6/7, 17/14) T .<br />
Příklad 15.2: Na obdélníku Ω = (0, 1/2) × (0, 1) s hranicí Γ řešte metodou sítí problém<br />
−∆u = −48 v Ω,<br />
u = 4(x + y) na Γ.<br />
V obou směrech volte diskretizační krok h = 1/4. (Pozor: Obecná sít’ová rovnice se někdy uvádí<br />
pro operátor −∆, jindy pro ∆; při výpočtech vyjděte ze správné varianty.)<br />
Řešení:<br />
4 5 6<br />
Sít’ová rovnice v uzlu (x i ,y j ) (pětibodové schéma):<br />
3<br />
u 3<br />
5<br />
− Uj i+1 − 2Uj i + Uj i−1<br />
h 2<br />
− Uj+1 i<br />
− 2U j i + Uj−1 i<br />
q 2 = f j i .<br />
2<br />
1<br />
u 2<br />
4<br />
u 1<br />
3<br />
Jestliže h = q (čtvercová sít’), pak<br />
−U j i+1 − Uj i−1 − Uj+1 i<br />
V našem značení (jest h 2 f j i = −3)<br />
− U j−1<br />
i<br />
+ 4U j i = h2 f j i .<br />
4u 1 − u 2 − 5 = −3,<br />
−u 1 + 4u 2 − u 3 − 6 = −3,<br />
−u 2 + 4u 3 − 13 = −3.<br />
0 1 2<br />
Maticově<br />
⎛<br />
4 −1 0 |<br />
⎞<br />
2<br />
⎛<br />
4 −1 0 |<br />
⎞<br />
2<br />
⎛<br />
4 −1 0 |<br />
⎞<br />
2<br />
⎝−1 4 −1 | 3 ⎠ ∼ ⎝0 15 −4 | 14⎠ ∼ ⎝0 15 −4 | 14 ⎠ ,<br />
0 −1 4 | 10 0 −1 4 | 10 0 0 56 | 164<br />
řešení (u 1 , u 2 , u 3 ) T = (13/14, 12/7, 41/14) T .<br />
Příklad 15.3: Necht’ Ω = (0,1) × (0,1). Okrajovou úlohu pro Poissonovu rovnici<br />
−∆u(x,y) = 3(x + y) v Ω,<br />
u(x,y) = 1 pro [x,y] ∈ ∂Ω<br />
řešte metodou sítí s krokem h = 1/3 v obou směrech.<br />
Řešení:<br />
71
Sít’ová rovnice v uzlu (x i ,y j ) (pětibodové schéma):<br />
1<br />
1 1<br />
1<br />
− Uj i+1 − 2Uj i + Uj i−1<br />
h 2<br />
− Uj+1 i<br />
− 2U j i + Uj−1 i<br />
q 2 = f j i .<br />
1<br />
u 1<br />
u 2<br />
1<br />
Jestliže h = q (čtvercová sít’), pak<br />
−U j i+1 − Uj i−1 − Uj+1 i<br />
− U j−1<br />
i<br />
+ 4U j i = h2 f j i .<br />
1<br />
u 3 u 4<br />
1<br />
V našem značení<br />
1 1 1 1<br />
−2 + 4u 1 − u 2 − u 3 = 3(1/3 + 2/3)/9,<br />
−2 − u 1 + 4u 2 − u 4 = 3(2/3 + 2/3)/9,<br />
−2 − u 1 + 4u 3 − u 4 = 3(1/3 + 1/3)/9,<br />
−2 − u 2 − u 3 + 4u 4 = 3(2/3 + 1/3)/9.<br />
Maticově (pak změna pořadí rovnic a změna znaménka)<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
4 −1 −1 0 | 7/3 1 0 −4 1 | −20/9<br />
⎜−1 4 0 −1 | 22/9<br />
⎟<br />
⎝−1 0 4 −1 | 20/9⎠ ∼ ... ∼ ⎜0 1 1 −4 | −7/3<br />
⎟<br />
⎝0 0 −4 8 | 43/9 ⎠ ;<br />
0 −1 −1 4 | 7/3 0 0 0 24 | 28<br />
řešení (u 1 , u 2 , u 3 , u 4 ) T = (7/6, 43/36, 41/36, 7/6) T .<br />
Příklad 15.4: Na obdélníku Ω = (0, 2) × (0, 1) s hranicí Γ řešte metodou sítí problém<br />
−∆u = 16(x + y) v Ω,<br />
u = 4xy na Γ.<br />
V obou směrech volte diskretizační krok h = 1/2. (Pozor: Obecná sít’ová rovnice se někdy uvádí<br />
pro operátor −∆, jindy pro ∆; při výpočtech vyjděte ze správné varianty.)<br />
Řešení:<br />
0<br />
2<br />
4<br />
6<br />
8<br />
0<br />
u 1 u 2 u 3 4 Správné hodnoty v uzlech na hranici.<br />
0 0 0 0 0<br />
Sít’ové rovnice v našem značení (pětibodové schéma)<br />
Odtud<br />
4u 1 − u 2 − 0 − 2 = 4,<br />
−u 1 + 4u 2 − u 3 − 0 − 4 = 6,<br />
−u 2 + 4u 3 − 4 − 6 − 0 = 8.<br />
u 1 = 37<br />
14 , u 2 = 32 7 , u 3 = 79<br />
14 .<br />
Příklad 15.5: Na obdélníku Ω = (−1, 3) × (−1, 1) s hranicí Γ řešte metodou sítí problém<br />
−∆u = x(y + 2) v Ω,<br />
u = x + 2y na Γ.<br />
72
V obou směrech volte diskretizační krok h = 1. (Pozor: Obecná sít’ová rovnice se někdy uvádí<br />
pro operátor −∆, jindy pro ∆; při výpočtech vyjděte ze správné varianty.)<br />
Řešení:<br />
1<br />
2<br />
3<br />
4<br />
5<br />
−1<br />
u 1 u 2 u 3 3 Správné hodnoty v uzlech na hranici.<br />
−3 −2 −1 0 1<br />
Sít’ové rovnice (pětibodové schéma) v našem značení<br />
4u 1 − u 2 − (−1) − (−2) − 2 = 0, tedy 4u 1 − u 2 = −1;<br />
−u 1 + 4u 2 − u 3 − (−1) − 3 = 2, tedy − u 1 + 4u 2 − u 3 = 4;<br />
−u 2 + 4u 3 − 3 − 0 − 4 = 4, tedy − u 2 + 4u 3 = 11.<br />
Odtud<br />
u 3 = 180<br />
56 = 45<br />
14 ,<br />
15u 2 = 15 + 4 45 105 + 90<br />
= = 195<br />
14 7 7 ⇒ u 2 = 13 7 ,<br />
4u 1 = −1 + 13 7 = 6 7 ⇒ u 1 = 3 14 .<br />
Příklad 15.6: Na obdélníku<br />
s hranicí Γ řešte metodou sítí problém<br />
Ω = {(x,y) ∈ R 2 : x ∈ (−1/4, 1/4), y ∈ (−1/2, 1/2)}<br />
−∆u(x,y) = 256y 2 − 15x 3 + 16 v Ω,<br />
u(x,y) = 48x 2 + 8y na Γ<br />
a vypočtěte přibližné řešení v bodě (0,1/4). V obou směrech volte diskretizační krok h = 1/4.<br />
(Upozornění: Vhodným očíslováním uzlů sítě se výpočet usnadní.)<br />
Řešení:<br />
5<br />
3<br />
1<br />
4<br />
u 3<br />
u 2<br />
u 1<br />
5<br />
3<br />
1<br />
V našem značení (pětibodové schéma)<br />
4u 1 − u 2 + 2 = 2,<br />
−u 1 + 4u 2 − u 3 − 6 = 1,<br />
−u 2 + 4u 3 − 14 = 2.<br />
−4<br />
Odtud u 3 = 268<br />
56 = 134<br />
28 = 67<br />
14 .<br />
Příklad 15.7: Necht’ Ω = {(x,y) ∈ R 2 : x ∈ (−1,1), y ∈ (−1,1)}. Níže uvedenou okrajovou<br />
úlohu pro Poissonovu rovnici řešte metodou sítí s krokem h = 2/3 v obou směrech. Neznámé<br />
73
zastupující přibližné hodnoty řešení označte dle schématu. Doporučení: Soustavu rovnic řešte<br />
Gaussovou eliminací, rovnice si nejdříve vhodně seřad’te, ušetříte si práci a počítání s velkými<br />
čísly.<br />
−∆u(x,y) = 27 4 x + 27<br />
2 y v Ω,<br />
u(x,y) = 3|x| + 3|y| − 4 pro (x,y) ∈ ∂Ω<br />
u 1<br />
u 2<br />
u 3 u 4<br />
Řešení:<br />
2<br />
0<br />
0 0<br />
u 1 u 2<br />
2<br />
0<br />
Hodnoty v uzlech na hranici (nejsou nutné hodnoty v rozích<br />
čtverce) – viz obr.<br />
Sít’ová rovnice v uzlu (x i ,y j ) (pětibodové schéma):<br />
0<br />
u 3 u 4<br />
0<br />
− Uj i+1 − 2Uj i + Uj i−1<br />
h 2<br />
− Uj+1 i<br />
Jestliže h = q (čtvercová sít’), pak<br />
− 2U j i + Uj−1 i<br />
q 2 = f j i .<br />
2 0 0 2<br />
−U j i+1 − Uj i−1 − Uj+1 i<br />
− U j−1<br />
i<br />
+ 4U j i = h2 f j i .<br />
V našem značení<br />
4u 1 − u 2 − u 3 = 4 ( 27 −1<br />
9 4 3 + 27 )<br />
1<br />
= 1,<br />
2 3<br />
−u 1 + 4u 2 − u 4 = 4 ( 27 1<br />
9 4 3 + 27 )<br />
1<br />
= 3,<br />
2 3<br />
−u 1 + 4u 3 − u 4 = 4 ( 27 −1<br />
9 4 3 + 27 )<br />
−1<br />
= −3,<br />
2 3<br />
−u 2 − u 3 + 4u 4 = 4 ( 27 1<br />
9 4 3 + 27 )<br />
−1<br />
= −1,<br />
2 3<br />
.<br />
Maticově (pak změna pořadí rovnic a změna znaménka)<br />
⎛<br />
⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
4 −1 −1 0 | 1 1 0 −4 1 | 3 1 0 −4 1 | 3<br />
⎜−1 4 0 −1 | 3<br />
⎟<br />
⎝−1 0 4 −1 | −3⎠ ∼ ⎜ 0 1 1 −4 | 1<br />
⎟<br />
⎝−1 4 0 −1 | 3⎠ ∼ ⎜0 1 1 −4 | 1<br />
⎟<br />
⎝0 4 −4 0 | 6 ⎠<br />
0 −1 −1 4 | −1 4 −1 −1 0 | 1 0 −1 15 −4 | −11<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 0 −4 1 | 3 1 0 −4 1 | 3<br />
∼ ⎜0 1 1 −4 | 1<br />
⎟<br />
⎝0 0 −8 16 | 2 ⎠ ∼ ⎜0 1 1 −4 | 1<br />
⎟<br />
⎝0 0 −8 16 | 2 ⎠ .<br />
0 0 16 −8 | −10 0 0 0 24 | −6<br />
Řešení (u 1 , u 2 , u 3 , u 4 ) T = (1/4, 3/4, −3/4, −1/4) T .<br />
74
16 Metoda sítí ve 2D: vlnová rovnice<br />
Příklad 16.1: Problém<br />
∂ 2 u<br />
∂t 2 = u<br />
4∂2 ∂x 2 v G = (0,2) × (0,5), (29)<br />
{<br />
x pro x ∈ (0,1),<br />
u(x,0) =<br />
(30)<br />
2 − x pro x ∈ (1,2)<br />
{<br />
∂u<br />
∂t (x,0) = x 2 pro x ∈ (0,1),<br />
(2 − x) 2 (31)<br />
pro x ∈ (1,2)<br />
u(0,t) = u(2,t) = 0, 0 ≤ t ≤ 5 (32)<br />
řešte metodou sítí s explicitním schématem a vypočtěte hodnotu přibližného řešení v bodech<br />
B 1 = (1, 1/2) a B 2 = (3/2, 1/2).<br />
Řešení: Nejsou předepsány diskretizační parametry h a τ, zvolíme je tedy tak, abychom snadno<br />
získali požadované hodnoty.<br />
Je patrné, že v prostorovém směru stačí zvolit h = 1/2. Pro diskretizaci proměnné t však<br />
nemůžeme zvolit τ = 1/2, protože body B 1 a B 2 by se sice staly uzly sítě, ale nebyla by splněna<br />
podmínka stability τ ≤ h/a (a 2 = 4, tj. a = 2). Proto volíme τ = 1/4.<br />
V uzlech sítě, jejichž prostorová souřadnice je rovna 0 nebo 2 je, podle (32), řešení rovno 0.<br />
Pro čas t 0 = 0 získáme hodnoty Ui 0 , i = 1,2,3, přibližného řešení z počáteční podmínky<br />
(30), viz obrázek níže; číselné hodnoty jsou připsány k uzlům.<br />
Pro čas t 1 = τ získáme hodnoty Ui 1 , i = 1,2,3, přibližného řešení z počátečních podmínek<br />
(30) a (31), tj. Ui 1 = Ui 0 + τ ∂u<br />
∂t (x i,0), viz [2, str. 79] nebo [5] a obrázek níže. (Hodnoty Ui 0 jsou<br />
již známy, τ = 1/4 a ∂u<br />
∂t (x i,0) je dáno předpisem (31).)<br />
Máme spočítat přibližné řešení v bodě B 1 , tj. hodnotu U2 2 . Použití pětibodového schématu<br />
vede k obecné diferenční rovnici<br />
Ui k+1 = 2<br />
(1 − a2 τ 2 )<br />
h 2 Ui k + a2 τ 2 ( )<br />
h 2 Ui+1 k + Ui−1<br />
k − Ui k−1 ,<br />
do níž dosadíme k = 1, i = 2, a = 2, h = 1/2, τ = 1/4, tím ji zjednodušíme. Dostaneme<br />
U2 2 = U1 3 + U1 1 − U0 2<br />
a vyčíslíme U2 2 = 9<br />
16 + 9 16 − 1 = 2 16 = 1 8 .<br />
Bodu B 2 odpovídá U3 2 . Stejným postupem zjistíme, že<br />
U3 2 = U1 4 + U1 2 − U0 3 = 0 + 5 4 − 1 2 = 3 4 ,<br />
protože z okrajové podmínky přímo dostáváme U 1 4 = 0 a hodnoty U1 2 a U0 2<br />
také známe.<br />
75
t 3<br />
0<br />
t 2<br />
U 2 2 U 2 3 0<br />
t 1<br />
0<br />
9<br />
16<br />
5<br />
4<br />
9<br />
16 0<br />
1<br />
2 1<br />
1<br />
2 0<br />
t 0 = 0<br />
x 0 = 0 x 1 x 2 x 3 x 4 = 2<br />
Příklad 16.2: Necht’ G = (0,2) × (0,1). Metodou sítí s explicitním pětibodovým schématem<br />
řešte úlohu s vlnovou rovnicí<br />
∂ 2 u<br />
∂t 2 = u<br />
4∂2 ∂x 2 v G,<br />
u(x,0) = 4x(2 − x) pro 0 < x < 2,<br />
∂u<br />
(x,0) = 0 pro 0 < x < 2<br />
∂t<br />
u(0,t) = u(2,t) = 0 pro 0 < t < 1.<br />
Proměnnou x diskretizujte s krokem h = 1/2. Krok τ pro diskretizaci proměnné t zvolte tak,<br />
abyste si výpočty pokud možno zjednodušili, ale aby zároveň metoda byla stabilní; svou volbu<br />
zdůvodněte. Vypočtěte přibližné řešení v čase t = 1.<br />
Řešení: Sít’ová rovnice v uzlu (x i ,t k ) (pětibodové schéma):<br />
U k+1<br />
i<br />
− 2U k i + U k−1<br />
i<br />
τ 2<br />
= a 2Uk i+1 − 2Uk i + U k i−1<br />
h 2 .<br />
Ze sít’ové rovnice plyne<br />
)<br />
Ui k+1 = 2<br />
(1 − τ 2 a2<br />
h 2 Ui k + τ 2 a2 ( )<br />
h 2 Ui+1 k + Uk i−1 − Ui k−1 .<br />
Zadání dává a 2 /h 2 = 4/(1/4) = 16. Volbou τ = 1/4 dostaneme 1 − τ 2 a2 = 0 při splnění<br />
h 2<br />
podmínky stability τ ≤ h/a = (1/2)/2 = 1/4.<br />
Použijeme tedy schéma<br />
U k+1<br />
i<br />
= U k i+1 + U k i−1 − U k−1<br />
i<br />
.<br />
76
Pro t = 1/4 (tj. k = 1) určíme uzlové hodnoty<br />
z počátečních podmínek. Protože počáteční<br />
rychlost je nulová, jest U 1 i = U 0 i = 4x i (2 − x i ),<br />
i = 0,1,2,3,4.<br />
Uzlové hodnoty pro t = 1/4: 0, 3, 4, 3, 0.<br />
Uzlové hodnoty pro t = 1/2: 0, 1, 2, 1, 0.<br />
Uzlové hodnoty pro t = 3/4: 0, −1, −2, −1, 0.<br />
Uzlové hodnoty pro t = 1: 0, −3, −4, −3, 0.<br />
0 −3 −4 −3 0<br />
0 −1 −2 −1 0<br />
0 1 2 1 0<br />
0 3 4 3 0<br />
0 3 4 3 0<br />
Příklad 16.3: Problém<br />
∂ 2 u<br />
∂t 2 = 1 ∂ 2 u<br />
4 ∂x 2 v Ω = (0,1) × (0,2),<br />
u(x,0) = 4x(1 − x) pro x ∈ (0,1),<br />
{<br />
∂u<br />
∂t (x,0) = 2x pro x ∈ (0,1/2],<br />
2(1 − x) pro x ∈ (1/2,1)<br />
u(0,t) = u(1,t) = 0, 0 < t < 2,<br />
řešte metodou sítí s explicitním schématem a vypočtěte hodnotu přibližného řešení v bodech<br />
B 0 = (0, 2), B 1 = (1/4, 2), B 2 = (1/2, 2), B 3 = (3/4, 2), B 4 = (1, 2) a Q = (3/4, 1/2).<br />
Diskretizační parametry h a τ si sami vhodně zvolte.<br />
Řešení: Vhodná volba je h = 1/4 a τ = 1/2, pak je splněna podmínka stability τ ≤ h/a, nebot’<br />
a = 1/2.<br />
Sít’ tedy bude mít pět uzlů v prostorovém směru a pět časových vrstev. Pro t = 0 jsou uzlové<br />
hodnoty dány počáteční podmínkou a jsou (od x 0 = 0 k x 4 = 1) tyto (0,3/4,1,3/4,0).<br />
Pro t = 1/2 z U 1 i = U 0 i + τ ∂u<br />
∂t (x i,0) dostaneme uzlové hodnoty (0,1,3/2,1,0), hodnota v<br />
bodě Q tedy je rovna 1.<br />
Explicitní schéma pro naši volbu h a τ jest<br />
U k+1<br />
i<br />
= U k i+1 + U k i−1 − U k−1<br />
i<br />
.<br />
Odtud snadno dostaneme hodnoty v dalších časových vrstvách.<br />
Pro t = 1: (0,3/4,1,3/4,0).<br />
Pro t = 3/2: (0,0,0,0,0).<br />
Pro t = 2: (0, −3/4, −1, −3/4,0), což jsou hodnoty v bodech B i .<br />
Příklad 16.4: Problém<br />
∂ 2 u<br />
∂t 2 = ∂2 u<br />
∂x 2 v Ω = (0,3) × (0,2),<br />
u(x,0) = 8x 2 (3 − x) pro x ∈ (0,3),<br />
{<br />
∂u<br />
∂t (x,0) = 8x pro x ∈ (0,1],<br />
(12 − 4x) pro x ∈ (1,3)<br />
u(0,t) = u(3,t) = 0, 0 < t < 2,<br />
77
řešte metodou sítí s explicitním schématem a vypočtěte hodnotu přibližného řešení v bodech<br />
B 1 = (5/2, 1) a B 2 = (3/2, 2). Diskretizační parametry h a τ si sami vhodně zvolte (vyberte<br />
výpočetně nejjednodušší možnost).<br />
Řešení:<br />
t = 2<br />
t = 1<br />
0 7 8 −3 −11 −7 0<br />
0 14 22 15 2 −2 0<br />
0 15 21 27 24 9 0<br />
0 7 20 30 34 26 0<br />
0 5 16 27 32 25 0<br />
x = 0<br />
1<br />
2<br />
1<br />
3<br />
2<br />
2<br />
5<br />
2<br />
x = 3<br />
Z prostorové souřadnice bodu B 1 je patrné, že<br />
h = 1/2. Z podmínky stability τ ≤ h/a pak<br />
plyne volba τ = 1/2, nebot’ a = 1.<br />
Sít’ — viz obr. vlevo. Pro t = 0 jsou uzlové<br />
hodnoty dány počáteční podmínkou a<br />
jsou tyto 0, 5, 16, 27, 32, 25, 0. Použitím<br />
Ui 1 = Ui 0 + τ ∂u<br />
∂t (x i,0) dostaneme uzlové hodnoty<br />
na další vrstvě: 0, 7, 20, 30, 34, 26, 0.<br />
V prvních dvou vrstvách k plnému zisku bodů stačí<br />
jen hodnoty tištěné kurzívou, viz předposlední odstavec<br />
řešení.<br />
Explicitní schéma pro naši volbu h a τ jest Ui<br />
k+1 = Ui+1 k + Uk i−1 − Uk−1 i<br />
.<br />
Odtud snadno dostaneme hodnoty v dalších časových vrstvách, viz obrázek. Hodnoty v bodech<br />
B 1 a B 2 jsou vyznačeny tučně, kurzívou jsou vysázeny hodnoty nutné ke zjištění hodnot v<br />
bodech B 1 a B 2 , není tedy nezbytné počítat hodnoty ve všech bodech sítě.<br />
Příklad 16.5: Problém<br />
∂ 2 u<br />
∂t 2 = u<br />
16∂2 ∂x 2 v Ω = (0,9) × (0,1),<br />
{<br />
2x 2 pro x ∈ [0,3],<br />
u(x,0) =<br />
27 − 3x pro x ∈ (3,9]<br />
{<br />
∂u<br />
∂t (x,0) = 4x pro x ∈ [0,6],<br />
72 − 8x pro x ∈ (6,9]<br />
u(0,t) = u(9,t) = 0, 0 ≤ t ≤ 1,<br />
řešte metodou sítí s explicitním pětibodovým schématem a vypočtěte hodnotu přibližného řešení<br />
v bodech B 1 = (4, 1) a B 2 = (6, 1). Diskretizační parametry h a τ si sami vhodně zvolte (vyberte<br />
výpočetně nejjednodušší vhodnou možnost).<br />
78
Řešení:<br />
t = 1<br />
19 21<br />
0 18 24 15 0<br />
t = 1 2<br />
t = 1 4<br />
0 16 11 23 22 18 14 7 0<br />
0 3 10 21 19 17 15 10 5 0<br />
0 2 8 18 15 12 9 6 3 0<br />
x = 0 1 2 3 4 5 6 7 8 x = 9<br />
Z prostorové souřadnice bodů B 1 , B 2 a z délky prostorového intervalu je patrné, že h = 1.<br />
Z podmínky stability τ ≤ h/a pak plyne volba τ = 1/4, nebot’ a = 4. 31<br />
Pro t = 0 jsou uzlové hodnoty dány počáteční podmínkou, viz obr.<br />
Použitím<br />
U 1 i = U 0 i + τ ∂u<br />
∂t (x i,0) =<br />
{<br />
U 0 i + 1 4 4x i = U 0 i + x i pro x i ∈ [0,6],<br />
U 0 i + 1 4 (72 − 8x) = U0 i + 18 − 2x i pro x i ∈ (6,9]<br />
dostaneme uzlové hodnoty pro t = 1/4, viz obr. (V prvních dvou vrstvách k plnému zisku bodů<br />
stačí jen hodnoty tištěné tučně, viz předposlední odstavec řešení.)<br />
Explicitní schéma pro naši volbu h a τ jest Ui<br />
k+1 = Ui+1 k + Uk i−1 − Uk−1 i<br />
.<br />
Odtud a z okrajových podmínek snadno dostaneme hodnoty v dalších časových vrstvách,<br />
viz obrázek. Tučně jsou vyznačeny hodnoty využité explicitním schématem ke zjištění hodnot v<br />
bodech B 1 a B 2 , není tedy nezbytné počítat hodnoty ve všech bodech sítě.<br />
Hodnota v bodě B 1 je 19, hodnota v bodě B 2 je 21.<br />
Příklad 16.6: Kmitání struny je modelováno matematickou úlohou<br />
∂ 2 u<br />
∂t 2 = u<br />
4∂2 ∂x 2 v Ω = {(x,t) ∈ R 2 : x ∈ (0,5), t ∈ (0,3)},<br />
u(x,0) = x(x − 5)(x − 6) pro 0 ≤ x ≤ 5,<br />
{<br />
∂u<br />
∂t (x,0) = 6x 2 pro x ∈ [0,2],<br />
40 − 8x pro x ∈ (2,5]<br />
u(0,t) = u(5,t) = 0, 0 ≤ t ≤ 3.<br />
Úlohu řešte přibližně metodou sítí s explicitním pětibodovým schématem a s prostorovým krokem<br />
h = 1. Časový krok τ vhodně vyberte z nabídky τ = 1/2, τ = 2/3 a τ = 1. Vypočtěte<br />
hodnotu přibližného řešení v bodě x = 2 v čase t = 3.<br />
31 Příliš velké τ v důsledku opomenutí podmínky stability přísně trestejte.<br />
79
Řešení:<br />
t = 3<br />
−38<br />
t = 5 2<br />
0 −8 −18 −24 −20 0<br />
t = 2<br />
t = 3 2<br />
t = 1<br />
t = 1 2<br />
0 −6 −6 −2 −1 0<br />
0 2 10 17 18 0<br />
0 16 25 30 18 0<br />
0 23 36 26 12 0<br />
Z podmínky stability τ ≤ h a<br />
plyne volba τ = 1/2, která<br />
vede na velmi jednoduchý výpočet<br />
uzlových hodnot. Volba τ = 1 nebo<br />
τ = 2/3 vede k nestabilitě, navíc<br />
τ = 2/3 ani nedává čas t = 3.<br />
Pro t = 0 jsou uzlové hodnoty<br />
dány počáteční podmínkou, viz obr.<br />
Stačí jen v bodech nutných pro<br />
další výpočet (vyznačeny tučně).<br />
0 20 24 18 8 0<br />
x = 0 1 2 3 4 x = 5<br />
Použitím<br />
U 1 i = U 0 i + τ ∂u<br />
∂t (x i,0) =<br />
{<br />
U 0 i + 1 2 6x2 i = U0 i + 3x2 i pro x i ∈ [0,2],<br />
U 0 i + 1 2 (40 − 8x) = U0 i + 20 − 4x i pro x i ∈ (2,4]<br />
dostaneme uzlové hodnoty pro t = 1/2, viz obr. (V prvních dvou vrstvách k plnému zisku bodů<br />
stačí jen hodnoty tištěné tučně, viz předposlední odstavec řešení.)<br />
Explicitní schéma pro naši volbu h a τ jest Ui<br />
k+1 = Ui+1 k + Uk i−1 − Uk−1 i<br />
.<br />
Odtud a z okrajových podmínek dostaneme hodnoty v dalších časových vrstvách a ve sledovaném<br />
bodě, viz obrázek.<br />
Tučně jsou vyznačeny hodnoty využité explicitním schématem ke zjištění hodnot ve vyšetřovaném<br />
bodě, není tedy nutné počítat hodnoty ve všech bodech sítě.<br />
Hodnota přibližného řešení v bodě x = 2 a v čase t = 3 je −38.<br />
17 Metoda sítí ve 2D: rovnice vedení tepla<br />
Příklad 17.1: Problém vedení tepla<br />
∂u<br />
∂t = 1 ∂ 2 u<br />
4 ∂x 2 v G = (0,2) × (0,1), (33)<br />
u(x,0) = 8 − 8(x − 1) 4 pro x ∈ [0,2], (34)<br />
u(0,t) = 2t pro t ∈ [0,1], (35)<br />
u(2,t) = 4t pro t ∈ [0,1], (36)<br />
řešte metodou sítí se čtyřbodovým implicitním schématem a vypočtěte hodnotu přibližného<br />
řešení v bodě x = 3/2 a v čase t = 1/2. Diskretizační parametry h a τ si sami vhodně zvolte<br />
(vyberte výpočetně nejjednodušší možnost).<br />
80
Řešení: Abychom mohli spočítat přibližné řešení v požadovaném bodě, musí tento bod být uzlem<br />
sítě. Schéma je nepodmíněně stabilní, takže volba délky kroku τ není omezena volbou hodnoty<br />
h. Vhodná volba je h = 1/2 a τ = 1/2, příslušná sít’ obsahuje zkoumaný bod (3/2,1/2), náleží<br />
mu označení U3 1.<br />
Sít’ tedy bude mít pět uzlů v prostorovém směru a tři časové vrstvy; nakreslete si obrázek.<br />
Počáteční podmínka (34) dává pro čas t = 0 tyto hodnoty řešení 0, 15/2, 8, 15/2, 0 (po řadě od<br />
x 0 = 0 k x 4 = 2).<br />
Pro t = 1/2 je u(0,1/2) = U0 1 = 2τ = 1 (viz (35)) a u(2,1/2) = U1 4 = 4τ = 2 (viz (36)).<br />
Implicitní schéma jest<br />
U k i − U k−1<br />
i<br />
τ<br />
První rovnice (x = 1/2, t = 1/2, a 2 = 1/4)<br />
Druhá rovnice (x = 1, t = 1/2)<br />
Třetí rovnice (x = 3/2, t = 1/2)<br />
= a 2Uk i−1 − 2Uk i + U k i+1<br />
h 2 .<br />
U1 1 − 15/2<br />
1<br />
= 1 1 − 2U1 1 + U1 2<br />
4<br />
1<br />
,<br />
2<br />
4<br />
4U1 1 − U1 2 = 16.<br />
U2 1 − 8<br />
1<br />
= 1 U1 1 − 2U1 2 + U1 3<br />
4<br />
1<br />
,<br />
2<br />
4<br />
−U1 1 + 4U2 1 − U3 1 = 16.<br />
U3 1 − 15/2<br />
1<br />
= 1 U2 1 − 2U1 3 + 2<br />
4<br />
1<br />
,<br />
2<br />
4<br />
−U2 1 + 4U1 3 = 17.<br />
Maticově<br />
⎛<br />
⎞ ⎛<br />
⎞ ⎛<br />
⎞<br />
4 −1 0 | 16 1 −4 1 | −16 1 −4 1 | −16<br />
⎝−1 4 −1 | 16⎠ ∼ ⎝−4 1 0 | −16⎠ ∼ ⎝0 −15 4 | −80⎠<br />
0 −1 4 | 17 0 −1 4 | 17 0 −1 4 | 17<br />
⎛<br />
⎞ ⎛<br />
⎞<br />
1 −4 1 | −16 1 −4 1 | −16<br />
∼ ⎝0 1 −4 | −17⎠ ∼ ⎝0 1 −4 | −17 ⎠ ,<br />
0 −15 4 | −80 0 0 −56 | −335<br />
odtud U 1 3 = 335<br />
56 .<br />
Poznámka: Rovnici vedení tepla je možné řešit i explicitním schématem, viz text Metoda sítí<br />
— základní schémata. Pak je ovšem nutné zvolit h a τ tak, aby byla splněna podmínka stability.<br />
Poté místo sestavování rovnic postupujeme analogicky jako například v příkladech s vlnovou<br />
rovnicí řešenou explicitním schématem: po stanovení uzlových hodnot z počáteční a okrajové<br />
podmínky vypočítáváme hodnoty ve vnitřních uzlech sítě podle explicitního schématu.<br />
Příklad 17.2: Problém vedení tepla<br />
∂u<br />
∂t = u<br />
a2∂2<br />
∂x 2 v G = (0,2) × (0,30),<br />
u(x,0) = 4 − 2x pro x ∈ (0,2),<br />
u(0,t) = 4 pro t ∈ (0,30),<br />
u(2,t) = 0 pro t ∈ (0,30),<br />
81
kde a 2 = 1, řešte přibližně metodou sítí. Prostorovou proměnnou x diskretizujte s krokem<br />
h = 1/2 a časovou proměnnou t diskretizujte s krokem τ = 1/4. Použijte implicitní čtyřbodové<br />
schéma. Úkoly:<br />
a) Sestavte soustavu sít’ových rovnic a vypočtěte přibližné řešení v čase t = 1/4.<br />
b) Určete přibližné řešení v čase t = 2/4. (Zdůvodněte.)<br />
c) Určete přibližné řešení v čase t = i/4, kde i = 3,4,5,... ,120. (Zdůvodněte.)<br />
d) Na základě přibližného řešení vyslovte hypotézu o vlastnostech funkce u a její parciální<br />
derivace ∂u/∂t na oblasti G. (Nápověda: Zvolte pevně ˆx ∈ (0,2) tak, aby (ˆx,mτ), kde m =<br />
0,1,2,... ,120, byly body sítě, a vyslovte hypotézu o průběhu funkce ω(t) ≡ u(ˆx,t). Pak hypotézu<br />
rozšiřte na průběh funkce ω(t) ≡ u(ˆx,t) pro libovolné ˆx ∈ (0,2), a nakonec na funkci u<br />
na oblasti G.)<br />
e) Předpokládejte platnost hypotézy a odpovídajícím způsobem přeformulujte (zjednodušte)<br />
výchozí problém vedení tepla; jinými slovy – napište okrajovou úlohu zohledňující vlastnosti<br />
tepelného pole odvozené z hypotézy.<br />
f) Najděte přesné řešení nové okrajové úlohy z bodu e) (tj. nikoliv přibližné získané numerickými<br />
metodami) a porovnejte je s počáteční podmínkou původní úlohy a s přibližným řešením<br />
z bodů a) – c).<br />
Řešení: a) Z počáteční podmínky: U 0 0 = 4, U0 1 = 3, U0 2 = 2, U0 3 = 1 a U0 4 = 0.<br />
Na další časové vrstvě: U 1 0 = 4 a U1 4 = 0.<br />
Obecná sít’ová rovnice<br />
U k i − U k−1<br />
i<br />
τ<br />
s využitím τ = 1/4, a 2 = 1 a h = 1/2 dává<br />
Odtud dostáváme soustavu<br />
Po dosazení<br />
tedy<br />
Maticově<br />
⎛<br />
⎝ 3 −1 0 | 7 ⎞<br />
−1 3 −1 | 2⎠ ∼<br />
0 −1 3 | 1<br />
řešení (3, 2, 1) T pro čas t = 1/4.<br />
= a 2Uk i+1 − 2Uk i + U k i−1<br />
h 2<br />
−U k i−1 + 3U k i − U k i+1 = U k−1<br />
i<br />
.<br />
−U 1 0 + 3U 1 1 − U 1 2 = U 0 1,<br />
−U 1 1 + 3U1 2 − U1 3 = U0 2 ,<br />
−U 1 2 + 3U 1 3 − U 1 4 = U 0 3.<br />
−4 + 3U 1 1 − U 1 2 = 3,<br />
−U 1 1 + 3U1 2 − U1 3 = 2,<br />
−U 1 2 + 3U 1 3 − 0 = 1,<br />
3U 1 1 − U 1 2 = 7,<br />
−U 1 1 + 3U1 2 − U1 3 = 2,<br />
−U 1 2 + 3U 1 3 = 1.<br />
⎛<br />
⎝ 3 −1 0 | 7 ⎞ ⎛<br />
0 8 −3 | 13⎠ ∼ ⎝ 3 −1 0 | 7 ⎞ ⎛<br />
0 8 −3 | 13⎠ ∼ ⎝ 3 −1 0 | 7 ⎞<br />
0 8 −3 | 13⎠;<br />
0 −1 3 | 1 0 −8 24 | 8 0 0 21 | 21<br />
82
) Vidíme, že pro čas t = 1/4 jsou uzlové hodnoty stejné jako pro čas t = 0. Při přechodu<br />
na další časovou vrstvu bychom museli sestavit a řešit stejnou soustavu rovnic, tudíž i pro čas<br />
t = 1/2 bude přibližné řešení (ve vnitřních uzlech odleva) (3, 2, 1) T .<br />
c) Stejná úvaha vede k závěru, že na všech časových vrstvách bude přibližné řešení stejné,<br />
tj. (4, 3, 2, 1, 0) T (zde psáno včetně hodnot v krajních uzlech, ale to není pro hodnocení studenta<br />
podstatné).<br />
d) Hypotéza: funkce u nezávisí na proměnné t, její parciální derivace ∂u/∂t je nulová.<br />
e) u ′′ = 0, u(0) = 4, u(2) = 0.<br />
f) u = c 1 x + c 2 , z okrajových podmínek c 2 = 4 a c 1 = −2, tedy u = 4 − 2x. Řešení se<br />
shoduje s počáteční podmínkou a v bodech x i = ih, kde i = 0,1,2,3,4, má stejnou hodnotu<br />
jako přibližné řešení v bodech (x i ,kτ), kde k = 1,2,... 120.<br />
Příklad 17.3: Problém<br />
∂u<br />
∂t = u<br />
2∂2 ∂x 2 v Ω = (0,9) × (0,1),<br />
u(x,0) = −x 2 + 8x + 9 pro 0 ≤ x ≤ 9,<br />
u(0,t) = 9 − 4t pro 0 ≤ t ≤ 1,<br />
u(9,t) = 8t pro 0 ≤ t ≤ 1<br />
řešte metodou sítí s explicitním čtyřbodovým schématem a vypočtěte hodnotu přibližného řešení<br />
v bodech B 1 = (5, 1) a B 2 = (6, 1). Diskretizační parametry h a τ si sami vhodně zvolte (vyberte<br />
výpočetně nejjednodušší vhodnou možnost).<br />
Řešení:<br />
t = 1<br />
20<br />
139<br />
8<br />
6 22 21 18<br />
55<br />
4 6<br />
t = 1 2<br />
7 22 23 22 19 14<br />
17<br />
2 4<br />
t = 1 4<br />
8 15 20 23 24 23 20 15 8 2<br />
9 16 21 24 25 24 21 16 9 0<br />
x = 0 1 2 3 4 5 6 7 8 x = 9<br />
Z prostorové souřadnice bodů B 1 , B 2 a z délky prostorového intervalu je patrné, že h = 1.<br />
Z podmínky stability τ ≤ h 2 /(2a 2 ) pak plyne volba τ = 1/4, nebot’ a 2 = 2. 32<br />
Pro t = 0 jsou uzlové hodnoty dány počáteční podmínkou, viz obr.<br />
Explicitní schéma pro naši volbu h a τ jest Ui k+1 = 1 (<br />
2 U<br />
k<br />
i+1 + Ui−1<br />
k )<br />
.<br />
Odtud a z okrajových podmínek snadno dostaneme hodnoty v dalších časových vrstvách,<br />
viz obrázek. Hodnoty využité explicitním schématem ke zjištění hodnot v bodech B 1 a B 2 jsou<br />
graficky odlišeny, není nezbytné počítat hodnoty ve všech bodech sítě.<br />
Hodnota v bodě B 1 je 20, hodnota v bodě B 2 je 139/8.<br />
32 Příliš velké τ v důsledku opomenutí podmínky stability přísně trestejte.<br />
83
Příklad 17.4: V pokusu zaměřeném na vedení tepla v kovové tyčce můžeme pomocí parametrů<br />
α a β ovlivňovat počáteční rozložení teploty a teplotu konců tyčky, viz matematický model:<br />
∂u<br />
∂t = 1 ∂ 2 u<br />
2 ∂x 2 v Ω = {(x,t) ∈ R 2 : x ∈ (0,5), t ∈ (0,8)}<br />
u(x,0) = α(5x − x 2 ) pro 0 ≤ x ≤ 5,<br />
u(0,t) = αt pro 0 ≤ t ≤ 8,<br />
u(5,t) = βt pro 0 ≤ t ≤ 8.<br />
Výpočtem nalezněte takové hodnoty α,β ∈ R, aby při výpočtu metodou sítí s explicitním<br />
čtyřbodovým schématem vycházela v čase t = 4 v bodě x = 1 teplota 26 jednotek a v bodě<br />
x = 3 teplota 15 jednotek. Prostorový krok h i časový krok τ vhodně zvolte.<br />
Řešení:<br />
t = 4<br />
13α<br />
2<br />
2<br />
11α<br />
2 +β<br />
2<br />
t = 3<br />
3α<br />
7<br />
2 α 2α + β<br />
t = 2<br />
3α 4α 2β<br />
t = 1<br />
α 5α 3α β<br />
0 4α 6α 0<br />
x = 0 1 2 3 4 x = 5<br />
Z prostorové souřadnice sledovaných bodů a z délky prostorového intervalu je patrné, že<br />
h = 1 je vhodná volba. Z podmínky stability τ ≤ h 2 /(2a 2 ) pak plyne volba τ = 1, nebot’ a 2 = 1 2 .<br />
Pro t = 0 jsou uzlové hodnoty dány počáteční podmínkou, viz obr. Stačí jen v bodech<br />
nutných pro další výpočet.<br />
Explicitní schéma pro naši volbu h a τ jest Ui k+1 = 1 (<br />
2 U<br />
k<br />
i+1 + Ui−1<br />
k )<br />
.<br />
Odtud a z okrajových podmínek snadno dostaneme hodnoty v dalších časových vrstvách,<br />
viz obrázek.<br />
13α<br />
2<br />
Má být = 26, odtud α = 8. Dále požadujeme<br />
2<br />
dostáváme 44 + β = 30, tudíž β = −14.<br />
11α<br />
2<br />
+ β<br />
2<br />
Příklad 17.5: Vedení tepla v kovové tyčce je modelováno matematickou úlohou<br />
∂u<br />
∂t = ∂2 u<br />
∂x 2 v Ω = {(x,t) ∈ R 2 : x ∈ (−2,3), t ∈ (0,2)}<br />
u(x,0) = 2x(x − 1) pro − 2 ≤ x ≤ 3,<br />
u(−2,t) = 12 + 4t pro 0 ≤ t ≤ 2,<br />
u(3,t) = 12 + 8t pro 0 ≤ t ≤ 2.<br />
= 15. Po dosazení α = 8<br />
Úlohu řešte přibližně metodou sítí s explicitním čtyřbodovým schématem a s prostorovým krokem<br />
h = 1. Časový krok τ vhodně vyberte z nabídky τ = 1/4, τ = 1/2 a τ = 1. Odpovězte na<br />
otázku, jaká je přibližná teplota v bodech x = −1 a x = 1, a to v čase t = 2.<br />
84
Řešení:<br />
t = 2<br />
t = 3 2<br />
t = 1<br />
t = 1 2<br />
12 9<br />
18 6 12<br />
8 4 20<br />
14 2 6<br />
12 4 0 12<br />
x = −2 −1 0 1 2 x = 3<br />
Z podmínky stability τ ≤ h2<br />
2a 2<br />
plyne volba τ = 1/2, která<br />
vede na velmi jednoduchý výpočet<br />
uzlových hodnot. Volba τ = 1/4<br />
je také možná, výsledná explicitní<br />
formule je však komplikovanější<br />
(doufám, že tato komplikovanost<br />
odradí od volby τ = 1/4, jinak<br />
to budeme muset přepočítat). Volba<br />
τ = 1 vede k nestabilitě.<br />
Pro t = 0 jsou uzlové hodnoty<br />
dány počáteční podmínkou, viz obr.<br />
Stačí jen v bodech nutných pro další<br />
výpočet.<br />
Explicitní schéma pro naši volbu h a τ jest Ui k+1 = 1 (<br />
2 U<br />
k<br />
i+1 + Ui−1<br />
k )<br />
.<br />
Odtud a z okrajových podmínek snadno dostaneme hodnoty v dalších časových vrstvách a<br />
ve sledovaných bodech, viz obrázek.<br />
Poznámka: Další řešené příklady předvádějící použití metody sítí k přibližnému řešení parciálních<br />
diferenciálních rovnic naleznete v [2].<br />
Literatura<br />
[1] K. Rektorys: Variační metody v inženýrských problémech a v problémech matematické fyziky,<br />
SNTL, Praha, 1974.<br />
[2] K. Rektorys: <strong>Matematika</strong> 43. Obyčejné a parciální diferenciální rovnice s okrajovými<br />
podmínkami 2. Vydavatelství ČVUT, 3. vydání, Praha, 2001.<br />
[3] O. Zindulka: <strong>Matematika</strong> 3. Česká technika – nakladatelství ČVUT, 1. vydání, Praha, 2007.<br />
[4] <strong>Matematika</strong> 4: Příručka přežití. Ke stažení na webových stránkách vyučujícícho.<br />
[5] Text k metodě sítí na webové stránce přednášejícího.<br />
85