Water and Solute Permeability of Plant Cuticles: Measurement and ...

246 8 Effects of Temperature on Sorption and Diffusion of Solutes and Penetration of Water
log k ∗
infinite
20
15
10
5
0
- 5
log k ∗
infinite = - 3.27 + (1.44E D 10 -3 /R)
MX
-10
0 2 4 6 8 10 12 14 16 18
CM
log k ∗
infinite = - 5.24 +(1.37E D 10 -3 /R)
Hedera helix/IAA
Enthalpy of diffusion x 10 -3 x R -1
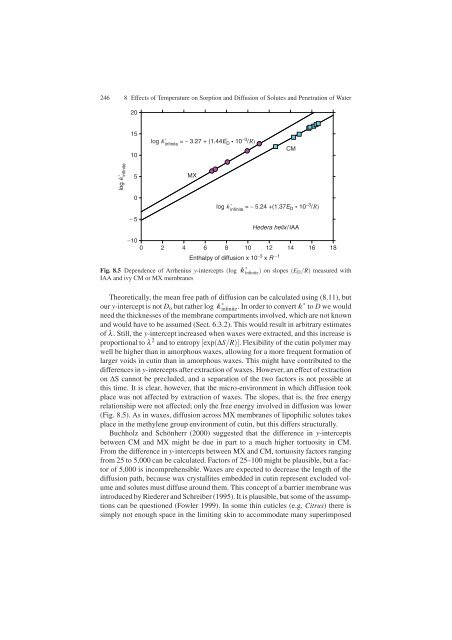
Fig. 8.5 Dependence of Arrhenius y-intercepts (log k ∗
infinite ) on slopes (ED/R) measured with
IAA and ivy CM or MX membranes
Theoretically, the mean free path of diffusion can be calculated using (8.11), but
our y-intercept is not Do but rather log k ∗ infinite. In order to convert k ∗ to D we would
need the thicknesses of the membrane compartments involved, which are not known
and would have to be assumed (Sect. 6.3.2). This would result in arbitrary estimates
of λ . Still, the y-intercept increased when waxes were extracted, and this increase is
proportional to λ 2 and to entropy [exp(∆S/R)]. Flexibility of the cutin polymer may
well be higher than in amorphous waxes, allowing for a more frequent formation of
larger voids in cutin than in amorphous waxes. This might have contributed to the
differences in y-intercepts after extraction of waxes. However, an effect of extraction
on ∆S cannot be precluded, and a separation of the two factors is not possible at
this time. It is clear, however, that the micro-environment in which diffusion took
place was not affected by extraction of waxes. The slopes, that is, the free energy
relationship were not affected; only the free energy involved in diffusion was lower
(Fig. 8.5). As in waxes, diffusion across MX membranes of lipophilic solutes takes
place in the methylene group environment of cutin, but this differs structurally.
Buchholz and Schönherr (2000) suggested that the difference in y-intercepts
between CM and MX might be due in part to a much higher tortuosity in CM.
From the difference in y-intercepts between MX and CM, tortuosity factors ranging
from 25 to 5,000 can be calculated. Factors of 25–100 might be plausible, but a factor
of 5,000 is incomprehensible. Waxes are expected to decrease the length of the
diffusion path, because wax crystallites embedded in cutin represent excluded volume
and solutes must diffuse around them. This concept of a barrier membrane was
introduced by Riederer and Schreiber (1995). It is plausible, but some of the assumptions
can be questioned (Fowler 1999). In some thin cuticles (e.g. Citrus) there is
simply not enough space in the limiting skin to accommodate many superimposed