2 - SAM - ETH Zürich

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
1.4
Anwendung auf kleine Zeitintervalle [t 0 ,t 1 ], [t 1 ,t 2 ], ..., [t N−1 , t N ] ➤ implizites Euler-Verfahren
y
1.2
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
exact solution
explicit Euler
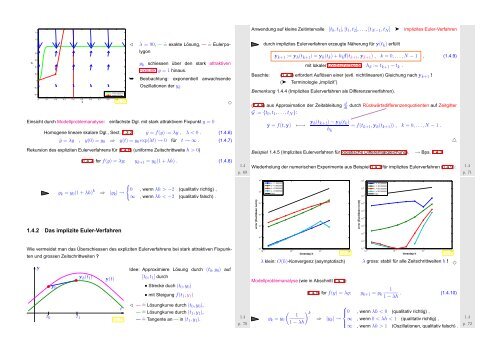
✁ λ = 90, — ˆ= exakte Lösung, — ˆ= Eulerpolygon
y k schiessen über den stark attraktiven
Fixpunkt y = 1 hinaus.
➥ Beobachtung: exponentiell anwachsende
Oszillationen der y k
durch implizites Eulerverfahren erzeugte Näherung für y(t k ) erfüllt
y k+1 := y h (t k+1 ) = y h (t k ) + h k f(t k+1 ,y k+1 ) , k = 0,...,N − 1 , (1.4.9)
mit lokaler (Zeit)schrittweite h k := t k+1 − t k .
Beachte: (1.4.9) erfordert Auflösen einer (evtl. nichtlinearen) Gleichung nach y k+1 !
(➤ Terminologie ”
implizit”)
Bemerkung 1.4.4 (Implizites Eulerverfahren als Differenzenverfahren).
t
Fig. 32
✸
(1.4.9) aus Approximation der Zeitableitung
dt d durch Rückwärtsdifferenzenquotienten auf Zeitgitter
G := {t 0 , t 1 ,...,t N }:
Einsicht durch Modellproblemanalyse: einfachste Dgl. mit stark attraktivem Fixpunkt y = 0
Homogene lineare skalare Dgl., Sect. 1.3.2 : ẏ = f(y) := λy , λ < 0 . (1.4.6)
ẏ = λy , y(0) = y 0 ⇒ y(t) = y 0 exp(λt) → 0 für t → ∞ . (1.4.7)
ẏ = f(t,y) ←→ y h(t k+1 ) − y h (t k )
h k
= f(t k+1 ,y h (t k+1 )) , k = 0,...,N − 1 .
△
Rekursion des expliziten Eulerverfahrens für (1.4.6) (uniforme Zeitschrittweite h > 0)
Beispiel 1.4.5 (Implizites Eulerverfahren für logistische Differentialgleichung). → Bps. 1.4.3
(1.4.2) for f(y) = λy: y k+1 = y k (1 + λh) . (1.4.8)
1.4
p. 69
Wiederholung der numerischen Experimente aus Beispiel 1.4.3 für implizites Eulerverfahren (1.4.9):
1.4
p. 71
y k = y 0 (1 + λh) k ⇒ |y k | →
{
0 , wenn λh > −2 (qualitativ richtig) ,
∞ , wenn λh < −2 (qualitativ falsch) .
10 0
λ = 1.000000
λ = 3.000000
λ = 6.000000
λ = 9.000000
O(h)
10 0
10 −2
λ = 10.000000
λ = 30.000000
λ = 60.000000
λ = 90.000000
O(h)
1.4.2 Das implizite Euler-Verfahren
error (Euclidean norm)
10 −1
10 −2
10 −3
error (Euclidean norm)
10 −4
10 −6
10 −8
10 −10
10 −12
10 −4
10 −14
Wie vermeidet man das Überschiessen des expliziten Eulerverfahrens bei stark attraktiven Fixpunkten
und grossen Zeitschrittweiten ?
y
y h (t 1 ) y(t)
y 0
t
t 0 t 1 Fig. 33
Idee: Approximiere Lösung durch (t 0 , y 0 ) auf
[t 0 ,t 1 ] durch
• Strecke duch (t 0 , y 0 )
• mit Steigung f(t 1 , y 1 )
✁ — ˆ= Lösungkurve durch (t 0 , y 0 ),
— ˆ= Lösungkurve durch (t 1 , y 1 ),
— ˆ= Tangente an — in (t 1 ,y 1 ).
1.4
p. 70
10 1 timestep h
10 −5
10 −3 10 −2 10 −1 10 0
λ klein: O(h)-Konvergenz (asymptotisch)
Fig. 34
Modellproblemanalyse (wie in Abschnitt 1.4.1):
( ) 1 k
y k = y 0 ⇒ |y
1 − λh k | →
10 2 timestep h
10 −16
10 −3 10 −2 10 −1 10 0
Fig. 35
λ gross: stabil für alle Zeitschrittweiten h !
(1.4.9) for f(y) = λy: y k+1 = y k
1
1 − λh . (1.4.10)
⎧
⎪⎨ 0 , wenn λh < 0 (qualitativ richtig) ,
∞ , wenn 0 < λh < 1 (qualitativ richtig) ,
⎪⎩
∞ , wenn λh > 1 (Oszillationen, qualitativ falsch) .
✸
1.4
p. 72