2 - SAM - ETH Zürich

Beobachtung aus Bsp. 2.4.7 einfach zu erklären, falls
y h (T) = y(T) + α 1 h 2 + α 2 h 4 + α 6 h 6 + · · · .
➣ DIFEX-Algorithmus [5, Sect. 4.3.3]
△
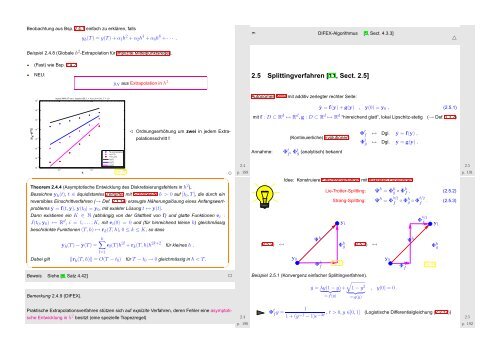
Beispiel 2.4.8 (Globale h 2 -Extrapolation für implizite Mittelpunktsregel).
(Fast) wie Bsp. 2.4.7
NEU:
y N aus Extrapolation in h 2
2.5 Splittingverfahren [11, Sect. 2.5]
Implicit MPR (h 2 extr.), logistic ODE, λ = 10.0, y0 = 0.01, T = 1.0
Autonomes AWP mit additiv zerlegter rechter Seite:
10 −2
10 −4
ẏ = f(y) + g(y) , y(0) = y 0 , (2.5.1)
mit f : D ⊂ R d ↦→ R d , g : D ⊂ R d ↦→ R d “hinreichend glatt”, lokal Lipschitz-stetig (→ Def. 1.3.2)
|y N
−y(T)|
10 0 h
10 −6
10 −8
✁ Ordnungserhöhung um zwei in jedem Extrapolationsschritt
!
(Kontinuierliche) Evolutionen:
Φ t f ↔ Dgl. ẏ = f(y) ,
Φ t g ↔ Dgl. ẏ = g(y) .
10 −10
✬
✫
10 −12
10 −14
No extrapolation
n=(1,2)
n=(1,2,3)
O(h 2 )
O(h 4 )
O(h 6 )
10 −2 10 −1 10 0
Fig. 66
Theorem 2.4.4 (Asymptotische Entwicklung des Diskretisierungsfehlers in h 2 ).
Bezeichne y h (t), t ∈ äquidistantes Zeitgitter mit Schrittweite h > 0 auf [t 0 , T], die durch ein
reversibles Einschrittverfahren (→ Def. 2.1.14) erzeugte Näherungslösung eines Anfangswertproblems
ẏ = f(t,y), y(t 0 ) = y 0 , mit exakter Lösung t ↦→ y(t).
Dann existieren ein K ∈ N (abhängig von der Glattheit von f) und glatte Funktionen e i :
J(t 0 ,y 0 ) ↦→ R d , i = 1,...,K, mit e i (0) = 0 und (für hinreichend kleine h) gleichmässig
beschränkte Funktionen (T,h) ↦→ r k (T, h), 0 ≤ k ≤ K, so dass
y h (T) − y(T) =
k∑
e l (T)h 2l + r k (T,h)h 2k+2 für kleines h .
l=1
Dabei gilt ‖r k (T, h)‖ = O(T − t 0 ) für T − t 0 → 0 gleichmässig in h < T .
Beweis. Siehe [5, Satz 4.42] ✷
Bemerkung 2.4.9 (DIFEX).
✸
✩
✪
2.4
p. 189
2.5
Annahme: Φ t f , Φt g (analytisch) bekannt p. 191
(2.5.2) ↔
Idee: Konstruiere Einschrittverfahren mit diskreten Evolutionen
y 1
Ψ h
Φ h g
y 0
Φ h f
Lie-Trotter-Splitting: Ψ h = Φ h g ◦ Φ h f , (2.5.2)
Strang-Splitting: Ψ h = Φ h/2
f ◦ Φ h g ◦ Φ h/2
f . (2.5.3)
Fig. 67
(2.5.3) ↔
Beispiel 2.5.1 (Konvergenz einfacher Splittingverfahren).
√
1 − y 2
ẏ = λy(1 − y) +
} {{ }
=:f(y)
} {{ }
=:g(y)
Φ h/2
f y 1
Ψ h Φ h g
y 0
, y(0) = 0 .
Φ h/2
f
Fig. 68
Praktische Extrapolationsverfahren stützen sich auf explizite Verfahren, deren Fehler eine asymptotische
Entwicklung in h 2 besitzt (eine spezielle Trapezregel)
2.4
p. 190
Φ t f y = 1
1 + (y −1 − 1)e −λt , t > 0,y ∈]0, 1] (Logistische Differentialgleichung (2.2.12)) 2.5
p. 192