2 - SAM - ETH Zürich

Da y, z beliebig, folgt die Behauptung.
Bemerkung 2.2.3 (Kollokationsverfahren und numerische Quadratur).
f(t,y) = f(t) & y 0 = 0 ➤ Numerische Quadratur (→ Vorlesung Numerische Methoden”)
”
t 1
∫
y(t 1 ) = f(t) dt ≈ h ∑ s
i=1 b jf(t 0 + c j h) = Quadraturformel
t 0
➞ c 1 ,...,c s ↔ Knoten (engl. nodes) einer Quadraturformel (z.B. Gauss-Punkte auf [0, 1]
b 1 ,...,b s ↔ Gewichte (engl. weights) einer Quadraturformel
✷
△
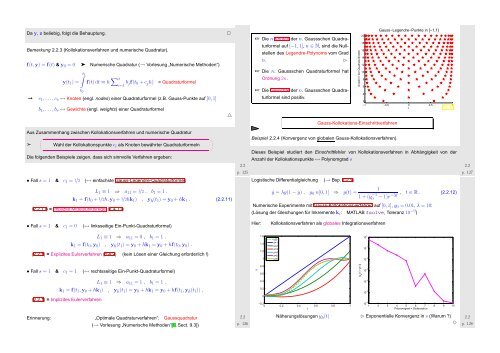
☞ Die n Knoten der n. Gaussschen Quadraturformel
auf [−1, 1], n ∈ N, sind die Nullstellen
des Legendre-Polynoms vom Grad
n. ✄
☞ Die n. Gaussschen Quadraturformel hat
Ordnung 2n.
☞ Die Gewichte der n. Gaussschen Quadraturformel
sind positiv.
Anzahl n der Quadraturknoten
Gauss-Kollokations-Einschrittverfahren
20
18
16
14
12
10
8
6
4
Gauss−Legendre−Punkte in [−1,1]
2
−1 −0.5 0 0.5 1
t
Fig. 57
Aus Zusammenhang zwischen Kollokationsverfahren und numerische Quadratur
✗
✔
➣ Wahl der Kollokationspunkte c i als Knoten bewährter Quadraturformeln
✖
✕
Die folgenden Beispiele zeigen, dass sich sinnvolle Verfahren ergeben:
• Fall s = 1 & c 1 = 1/2 (↔ einfachste Gauss-Legendre-Quadraturformel)
L 1 ≡ 1 ⇒ a 11 = 1/2 , b 1 = 1 .
k 1 = f(t 0 + 1/2h,y 0 + 1/2hk 1 ) , y h (t 1 ) = y 0 + hk 1 . (2.2.11)
(2.2.11) = Implizite Mittelpunktsregel (1.4.11)
2.2
p. 125
Beispiel 2.2.4 (Konvergenz von globalen Gauss-Kollokationsverfahren).
Dieses Beispiel studiert den Einschrittfehler von Kollokationsverfahren in Abhängigkeit von der
Anzahl der Kollokationspunkte ↔ Polynomgrad s
Logistische Differentialgleichung (→ Bsp. 1.2.1)
ẏ = λy(1 − y) , y 0 ∈]0, 1[ ⇒ y(t) =
1
1 + (y0 −1 , t ∈ R . (2.2.12)
− 1)e−λt Numerische Experimente mit Gauss-Kollokationsverfahren auf [0, 1], y 0 = 0.01, λ = 10:
(Lösung der Gleichungen für Inkremente k i : MATLAB fsolve, Toleranz 10 −9 )
2.2
p. 127
• Fall s = 1 & c 1 = 0 (↔ linksseitige Ein-Punkt-Quadraturformel)
Hier:
Kollokationsverfahren als globales Integrationsverfahren
L 1 ≡ 1 ⇒ a 11 = 0 , b 1 = 1 .
k 1 = f(t 0 ,y 0 ) , y h (t 1 ) = y 0 + hk 1 = y 0 + hf(t 0 ,y 0 ) .
(2.2.1) = Explizites Eulerverfahren (1.4.2) (kein Lösen einer Gleichung erforderlich !)
1.6
1.4
1.2
1
y(t)
s=1
s=2
s=3
s=4
s=5
s=6
10 0 Polynomgrad = Stufenzahl s
10 −1
10 −2
• Fall s = 1 & c 1 = 1 (↔ rechtsseitige Ein-Punkt-Quadraturformel)
L 1 ≡ 1 ⇒ a 11 = 1 , b 1 = 1 .
k 1 = f(t 1 ,y 0 + hk 1 ) , y h (t 1 ) = y 0 + hk 1 = y 0 + hf(t 1 ,y h (t 1 )) .
(2.2.1) = Implizites Eulerverfahren
Erinnerung:
Optimale Quadraturverfahren”: Gaussquadratur
2.2
”
(→ Vorlesung Numerische Methoden”[6, Sect. 9.3]) p. 126
”
y
0.8
0.6
0.4
0.2
0
−0.2
0 0.2 0.4 0.6 0.8 1
t
Näherungslösungen y h (t)
|y h
(1)−y(1)|
10 −3
10 −4
10 −5
10 −6
1 2 3 4 5 6 7 8 9 10
✄ Exponentielle Konvergenz in s (Warum ?)
2.2
✸ p. 128