2 - SAM - ETH Zürich
2 - SAM - ETH Zürich
2 - SAM - ETH Zürich
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
1.5<br />
1.5<br />
Verallgemeinerung: Eine gewöhnliche Differentialgleichung n-ter Ordnung, n ∈ N:<br />
y (n) = f(t,y,ẏ,...,y (n−1) ) . (1.1.4)<br />
y<br />
1<br />
y<br />
1<br />
✎ Notation: Superscript<br />
(n) ˆ= n. Ableitung nach der Zeit t<br />
0.5<br />
0<br />
0 0.5 1 1.5<br />
t<br />
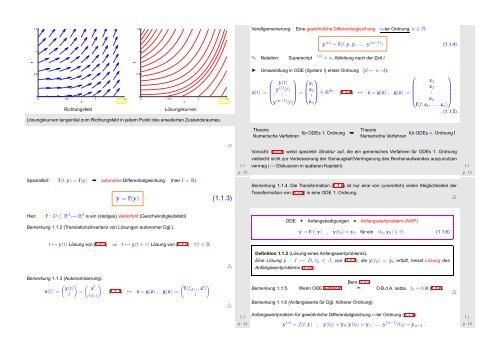
Fig. 1<br />
Richtungsfeld<br />
0.5<br />
0<br />
0 0.5 1 1.5<br />
t<br />
Fig. 2<br />
Lösungskurven<br />
Lösungskurven tangential zum Richtungsfeld in jedem Punkt des erweiterten Zustandsraumes.<br />
➤ Umwandlung in ODE (System !) erster Ordnung (d ← n · d):<br />
⎛ ⎞<br />
⎛ ⎞ ⎛ ⎞<br />
y(t)<br />
z<br />
z 2<br />
1<br />
z(t) := ⎜ y (1) (t)<br />
⎟<br />
⎝ . ⎠ = ⎜z 2<br />
⎟<br />
⎝ . ⎠ ∈ z 3<br />
Rdn : (1.1.4) ↔ ż = g(z) , g(z) :=<br />
⎜ .<br />
⎟<br />
y (n−1) ⎝ z<br />
(t) z n ⎠ .<br />
n<br />
f(t,z 1 , ...,z n )<br />
(1.1.5)<br />
Theorie<br />
Theorie<br />
für ODEs 1. Ordnung ➥ für ODEs n. Ordnung !<br />
Numerische Verfahren Numerische Verfahren<br />
✸<br />
1.1<br />
p. 13<br />
Vorsicht: (1.1.5) weist spezielle Struktur auf, die ein generisches Verfahren für ODEs 1. Ordnung<br />
vielleicht nicht zur Verbesserung der Genauigkeit/Verringerung des Rechenaufwandes auszunutzen<br />
vermag (→ Diskussion in späteren Kapiteln)<br />
1.1<br />
p. 15<br />
Spezialfall: f(t,y) = f(y) ➡ autonome Differentialgleichung (hier I = R)<br />
ẏ = f(y) . (1.1.3)<br />
Bemerkung 1.1.4. Die Transformation (1.1.5) ist nur eine von (unendlich) vielen Möglichkeiten der<br />
Transformation von (1.1.4) in eine ODE 1. Ordnung.<br />
△<br />
Hier: f : D ⊂ R d ↦→ R d is ein (stetiges) Vektorfeld (Geschwindigkeitsfeld)<br />
Bemerkung 1.1.2 (Translationsinvarianz von Lösungen autonomer Dgl.).<br />
ODE + Anfangsbedigungen = Anfangswertproblem (AWP)<br />
ẏ = f(t,y) , y(t 0 ) = y 0 für ein (t 0 ,y 0 ) ∈ Ω . (1.1.6)<br />
t ↦→ y(t) Lösung von (1.1.3) ⇒ t ↦→ y(t + τ) Lösung von (1.1.3) ∀τ ∈ R<br />
△<br />
Definition 1.1.2 (Lösung eines Anfangswertproblems).<br />
Eine Lösung y : J ↦→ D, t 0 ∈ J, von (1.1.1), die y(t 0 ) = y 0 erfüllt, heisst Lösung des<br />
Anfangswertproblems (1.1.6).<br />
Bemerkung 1.1.3 (Autonomisierung).<br />
( )<br />
y(t)<br />
z(t) := =<br />
t<br />
(<br />
z ′<br />
z d+1<br />
)<br />
: (1.1.1) ↔ ż = g(z) , g(z) :=<br />
(<br />
f(zd+1 ,z ′ )<br />
)<br />
.<br />
1<br />
Bemerkung 1.1.5.<br />
Wenn ODE autonom<br />
Bem. 1.1.2<br />
➣ O.B.d.A. setze t 0 = 0 in (1.1.6)<br />
△<br />
△<br />
Bemerkung 1.1.6 (Anfangswerte für Dgl. höherer Ordnung).<br />
1.1<br />
p. 14<br />
Anfangswertproblem für gewöhnliche Differentialgleichung n-ter Ordnung (1.1.4):<br />
y (n) = f(t,y) , y(t 0 ) = y 0 ,ẏ(t 0 ) = y 1 , . ..,y (n−1) (t 0 ) = y n−1 . p. 16<br />
1.1