2 - SAM - ETH Zürich

2.4.2 Extrapolationsidee
Erinnerung (→ Vorlesung ”
Numerische Methoden”): Romberg-Quadratur (→ [6, Sect. 9.4])
Abstrakter Rahmen:
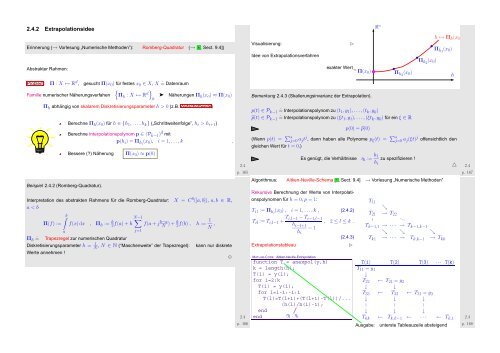
Visualisierung:
Idee von Extrapolationsverfahren
✄
exakter Wert
Π(x 0 )
R d
Π h3 (x 0 )
h ↦→ Π h (x 0 )
Π h1 (x 0 )
Π h2 (x 0 )
h
Problem: Π : X ↦→ R d , gesucht Π(x 0 ) für festes x 0 ∈ X, X ˆ= Datenraum
{
Familie numerischer Näherungsverfahen Π h : X ↦→ R d} h ➤ Näherungen Π h(x o ) ≈ Π(x 0 )
Bemerkung 2.4.3 (Skalierungsinvarianz der Extrapolation).
Π h abhängig von skalarem Diskretisierungsparameter h > 0 (z.B. Zeitschrittweite)
Berechne Π h (x 0 ) für h ∈ {h 1 , . ..,h k } ( ”
Schrittweitenfolge”, h i > h i+1 )
Berechne Interpolationspolynom p ∈ (P k−1 ) d mit
p(h i ) = Π hi (x 0 ), i = 1,...,k .
Bessere (?) Näherung
Beispiel 2.4.2 (Romberg-Quadratur).
Π(x 0 ) ≈ p(0)
Interpretation des abstrakten Rahmens für die Romberg-Quadratur: X = C 0 ([a,b]), a,b ∈ R,
a < b
Π h ˆ=
∫b
Π(f) :=
a
N−1
f(x) dx , Π h := h 2 f(a) + h ∑
Trapezregel zur numerischen Quadratur
j=1
f(a + j b−a
N ) + h 2 f(b) , h := 1 N ,
Diskretisierungsparameter h = N 1 , N ∈ N (“Maschenweite” der Trapezregel):
Werte annehmen !
kann nur diskrete
✸
2.4
p. 165
2.4
p. 166
p(t) ∈ P k−1 ˆ= Interpolationspolynom zu (t 1 ,y 1 ), ...,(t k ,y k )
˜p(t) ∈ P k−1 ˆ= Interpolationspolynom zu (ξt 1 ,y 1 ), ...,(ξt k ,y k ) für ein ξ ∈ R
p(0) = ˜p(0)
(Wenn p(t) = ∑ s
j=0 a j t j , dann haben alle Polynome p ξ (t) = ∑ s
j=0 a j (ξt) j offensichtlich den
gleichen Wert für t = 0.)
Es genügt, die Verhältnisse η i := h 1
h i
zu spezifizieren !
Algorithmus: Aitken-Neville-Schema [6, Sect. 9.4] → Vorlesung ”
Numerische Methoden”
Rekursive Berechnung der Werte von Interpolationspolynomen
für h = 0, p = 1:
T i1 := Π hi (x 0 ) , i = 1, ...,k , (2.4.2)
T il := T i,l−1 + T i,l−1 − T i−1,l−1
h i−l+1
h i
− 1
Extrapolationstableau
, 2 ≤ l ≤ k .
(2.4.3)
MATLAB-CODE : Aitken-Neville-Extrapolation
function T = anexpol(y,h)
k = length(h);
T(1) = y(1);
for i=2:k
T(i) = y(i);
for l=i-1:-1:1
T(l)=T(l+1)+(T(l+1)-T(l))/...
end
end
(h(l)/h(i)-1);
η l : η i
✄
T 11
ց
T 21
.
→ T 22
. ..
T k−1,1 → · · · → T k−1,k−1
ց ց ց
T k1 → · · · → T k,k−1 → T kk
△
2.4
p. 167
T(1) T(2) T(3) · · · T(k)
T 11 = y 1
↓
T 22 ← T 21 = y 2
↓ ↓
T 33 ← T 32 ← T 31 = y 3
↓ ↓ ↓
.
.
.
↓ ↓ ↓
T kk ← T k,k−1 ← · · · ← T k,1 2.4
Ausgabe: unterste Tableauzeile absteigend p. 168