2 - SAM - ETH Zürich

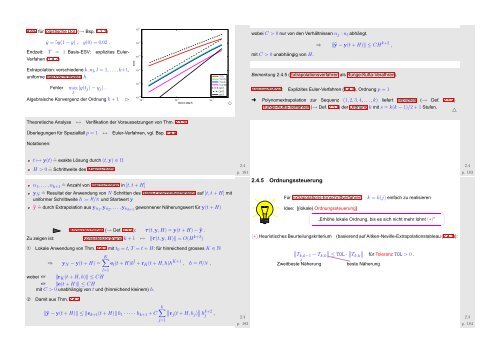
AWP für logistische Dgl. (→ Bsp. 1.2.1)
ẏ = 5y(1 − y) , y(0) = 0.02 .
Endzeit: T = 1 Basis-ESV: explizites Euler-
Verfahen (1.4.2)
Extrapolation: verschiedene k,n l , l = 1, ...,k+1,
uniforme Makroschrittweite h
Fehler
max |y(t j ) − y j | .
j
10 0
10 −2
10 −4
10 −6
10 −8
macro step h
10
Algebraische Konvergenz der Ordnung k + 1 ✄ −10
10 −3 10 −2 10 −1
error
(1,2)
(1,2,3)
(1,2,4)
(1,4,16)
O(h 2 )
O(h 3 )
O(h 4 )
✸
wobei C > 0 nur von den Verhältnissen n j : n l abhängt.
⇒ ‖ŷ − y(t + H)‖ ≤ CH k+2 ,
mit C > 0 unabhängig von H.
Bemerkung 2.4.5 (Extrapolationsverfahren als Runge-Kutta-Verafhren).
Basisverfahren: Explizites Euler-Verfahren (1.4.2), Ordnung p = 1
➜ Polynomextrapolation zur Sequenz (1, 2, 3, 4, ...,k) liefert explizites (→ Def. 2.1.2)
Runge-Kutta-Verfahren (→ Def. 2.3.1) der Ordnung k mit s = k(k − 1)/2 + 1 Stufen.
△
Theoretische Analyse ↔ Verifikation der Voraussetzungen von Thm. 2.1.10
Überlegungen für Spezialfall p = 1 ↔ Euler-Verfahren, vgl. Bsp. 2.4.4
Notationen:
t ↦→ y(t) ˆ= exakte Lösung durch (t,y) ∈ Ω
H > 0 ˆ= Schrittweite des Makroschritts
n 1 , ...,n k+1 ˆ= Anzahl von Mikroschritten in [t, t + H]
2.4
p. 181
2.4.5 Ordnungssteuerung
2.4
p. 183
y N ˆ= Resultat der Anwendung von N Schritten des Basis-Einschrittverfahrens auf [t,t + H] mit
uniformer Schrittweite h := H/N und Startwert y
Für Extrapolations-Einschrittverfahren:
k = k(j) einfach zu realisieren
ŷ ˆ= durch Extrapolation aus y n1 ,y n2 ,...,y nk+1 gewonnener Näherungswert für y(t + H)
Idee: [(lokale) Ordnungssteuerung]
✗
✔
Konsistenzfehler (→ Def. 2.1.7): τ(t,y,H) = y(t + H) − ŷ .
Zu zeigen ist: Konsistenzordnung k + 1 ↔ ‖τ(t,y, H)‖ = O(H k+2 )
✖
Erhöhe lokale Ordnung, bis es sich nicht mehr lohnt (∗)”
”
(∗) Heuristisches Beurteilungskriterium (basierend auf Aitken-Neville-Extrapolationstableau (2.4.3)):
✕
➀
Lokale Anwendung von Thm. 2.4.3 mit t 0 = t, T = t + H: für hinreichend grosses K ∈ N
⇒ y N − y(t + H) =
l=1
wobei ☞ ‖r K (t + H,h)‖ ≤ CH
☞ ‖e(t + H)‖ ≤ CH
mit C > 0 unabhängig von t und (hinreichend kleinem) h.
K∑
e l (t + H)h l + r K (t + H,h)h K+1 , h = H/N ,
∥
∥T k,k−1 − T k,k
∥ ∥ ≤ TOL · ∥∥T k,k
∥ ∥ für ToleranzTOL > 0 .
Zweitbeste Näherung
beste Näherung
➁ Damit aus Thm. 2.4.2
k∑ ∥
‖ŷ − y(t + H)‖ ≤ ‖e k+1 (t + H)‖ h 1 · · · · · h k+1 + C ∥r j (t + H, h j ) ∥ ∥h k+2
j ,
j=1
2.4
p. 182
2.4
p. 184