2 - SAM - ETH Zürich

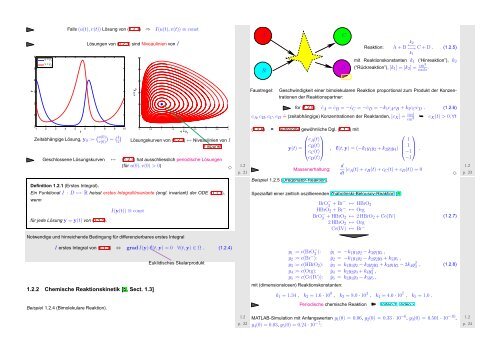
Falls (u(t), v(t)) Lösung von (1.2.3) ⇒ I(u(t),v(t)) ≡ const
Lösungen von (1.2.3) sind Niveaulinien von I
A
C
Reaktion:
k 2
A + B
←−
−→ C + D . (1.2.5)
k1
6
5
4
u = y 1
v = y 2
6
5
4
B
D
Fig. 5
mit Reaktionskonstanten k 1 (‘Hinreaktion”), k 2
(“Rückreaktion”), [k 1 ] = [k 2 ] = cm3
mol s .
y
3
v = y 2
3
Faustregel:
Geschwindigkeit einer bimolekularen Reaktion proportional zum Produkt der Konzentrationen
der Reaktionspartner:
2
1
2
1
for (1.2.5): ċ A = ċ B = −ċ C = −ċ D = −k 1 c A c B + k 2 c C c D . (1.2.6)
c A , c B , c C ,c D ˆ= (zeitabhängige) Konzentrationen der Reaktanden, [c X ] = mol
cm 3 ➥ c X (t) > 0; ∀t
0
1 2 3 4 5 6 7 8 9 10
t
Zeitabhängige Lösung, y 0 := ( u(0)
v(0)
)
=
( 42 )
0
0 0.5 1 1.5 2 2.5 3 3.5 4
u = y 1
Lösungskurven von (1.2.3) ↔ Niveaulinien von I
Fixpunkt
Geschlossene Lösungskurven ↔ (1.2.3) hat ausschliesslich periodische Lösungen
(für u(0),v(0) > 0)
Definition 1.2.1 (Erstes Integral).
Ein Funktional I : D ↦→ R heisst erstes Integral/Invariante (engl. invariant) der ODE (1.1.1),
wenn
für jede Lösung y = y(t) von (1.1.1).
I(y(t)) ≡ const
Notwendige und hinreichende Bedingung für differenzierbares erstes Integral
1.2
✸
p. 21
(1.2.6) = autonome gewöhnliche Dgl. (1.1.3) mit
⎛ ⎞
⎛ ⎞
c A (t)
1
y(t) = ⎜c B (t)
⎟
⎝c C (t) ⎠ , f(t,y) = (−k 1y 1 y 2 + k 2 y 3 y 4 ) ⎜ 1
⎟
⎝−1⎠ c D (t)
−1
Massenerhaltung:
Beispiel 1.2.5 (Oregonator-Reaktion).
d
dt (c A(t) + c B (t) + c C (t) + c D (t)) = 0
Spezialfall einer zeitlich oszillierenden Zhabotinski-Belousov-Reaktion [8]:
BrO − 3 + Br− ↦→ HBrO 2
HBrO 2 + Br − ↦→ Org
BrO − 3 + HBrO 2 ↦→ 2 HBrO 2 + Ce(IV)
(1.2.7)
2 HBrO 2 ↦→ Org
Ce(IV) ↦→ Br −
✸
1.2
p. 23
I erstes Integral von (1.1.1) ⇔ grad I(y) ·f(t,y) = 0 ∀(t,y) ∈ Ω . (1.2.4)
Euklidisches Skalarprodukt
1.2.2 Chemische Reaktionskinetik [5, Sect. 1.3]
Beispiel 1.2.4 (Bimolekulare Reaktion).
1.2
p. 22
y 1 := c(BrO − 3 ): ẏ 1 = −k 1 y 1 y 2 − k 3 y 1 y 3 ,
y 2 := c(Br − ): ẏ 2 = −k 1 y 1 y 2 − k 2 y 2 y 3 + k 5 y 5 ,
y 3 := c(HBrO 2 ): ẏ 3 = k 1 y 1 y 2 − k 2 y 2 y 3 + k 3 y 1 y 3 − 2k 4 y3 2 ,
y 4 := c(Org): ẏ 4 = k 2 y 2 y 3 + k 4 y3 2 ,
y 5 := c(Ce(IV)): ẏ 5 = k 3 y 1 y 3 − k 5 y 5 ,
mit (dimensionslosen) Reaktionskonstanten:
k 1 = 1.34 , k 2 = 1.6 · 10 9 , k 3 = 8.0 · 10 3 , k 4 = 4.0 · 10 7 , k 5 = 1.0 .
Periodische chemische Reaktion ➽ Video 1, Video 2
(1.2.8)
MATLAB-Simulation mit Anfangswerten y 1 (0) = 0.06, y 2 (0) = 0.33 · 10 −6 , y 3 (0) = 0.501 · 10 −10 , 1.2
y 4 (0) = 0.03, y 5 (0) = 0.24 · 10 −7 : p. 24