Bose-Einstein Condensates in Rotating Traps and Optical ... - BEC

72 Stationary states of a BEC in an optical lattice
which follows from µ(k) =∂(nε(k))/∂n. The two effective masses are in general different
from each other reflecting the difference in the Bloch band spectra. To give an example, for
s =10,gn=0.5ER one finds that m ∗ is about 28% larger than m ∗ µ.
Even though the expressions (6.17,6.18,6.19) are the same as for a single particle, the
results obtained are generally different since the energy Bloch bands do change in the presence
of interactions. Consequently, current, group velocity and effective mass not only depend on
lattice depth, but also on density.
2m¯v/qB
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
¯hk/qB
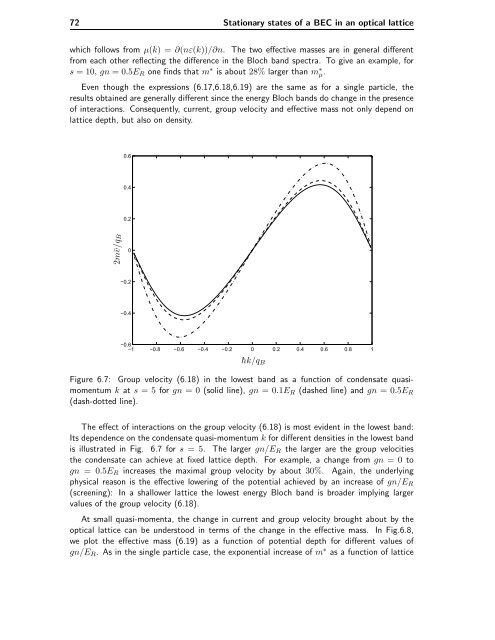
Figure 6.7: Group velocity (6.18) in the lowest band as a function of condensate quasimomentum
k at s =5for gn =0(solid line), gn =0.1ER (dashed line) and gn =0.5ER
(dash-dotted line).
The effect of interactions on the group velocity (6.18) is most evident in the lowest band:
Its dependence on the condensate quasi-momentum k for different densities in the lowest band
is illustrated in Fig. 6.7 for s =5. The larger gn/ER the larger are the group velocities
the condensate can achieve at fixed lattice depth. For example, a change from gn =0to
gn = 0.5ER increases the maximal group velocity by about 30%. Again, the underlying
physical reason is the effective lowering of the potential achieved by an increase of gn/ER
(screening): In a shallower lattice the lowest energy Bloch band is broader implying larger
values of the group velocity (6.18).
At small quasi-momenta, the change in current and group velocity brought about by the
optical lattice can be understood in terms of the change in the effective mass. In Fig.6.8,
we plot the effective mass (6.19) as a function of potential depth for different values of
gn/ER. As in the single particle case, the exponential increase of m ∗ as a function of lattice