Bose-Einstein Condensates in Rotating Traps and Optical ... - BEC
Bose-Einstein Condensates in Rotating Traps and Optical ... - BEC
Bose-Einstein Condensates in Rotating Traps and Optical ... - BEC
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
88 Bogoliubov excitations of Bloch state condensates<br />
¯hω/ER<br />
1.2<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1<br />
¯hq/qB<br />
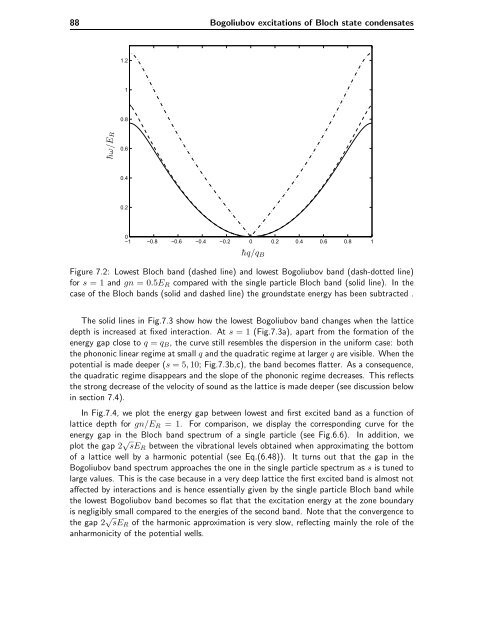
Figure 7.2: Lowest Bloch b<strong>and</strong> (dashed l<strong>in</strong>e) <strong>and</strong> lowest Bogoliubov b<strong>and</strong> (dash-dotted l<strong>in</strong>e)<br />
for s =1<strong>and</strong> gn =0.5ER compared with the s<strong>in</strong>gle particle Bloch b<strong>and</strong> (solid l<strong>in</strong>e). In the<br />
case of the Bloch b<strong>and</strong>s (solid <strong>and</strong> dashed l<strong>in</strong>e) the groundstate energy has been subtracted .<br />
The solid l<strong>in</strong>es <strong>in</strong> Fig.7.3 show how the lowest Bogoliubov b<strong>and</strong> changes when the lattice<br />
depth is <strong>in</strong>creased at fixed <strong>in</strong>teraction. At s =1(Fig.7.3a), apart from the formation of the<br />
energy gap close to q = qB, the curve still resembles the dispersion <strong>in</strong> the uniform case: both<br />
the phononic l<strong>in</strong>ear regime at small q <strong>and</strong> the quadratic regime at larger q are visible. When the<br />
potential is made deeper (s =5, 10; Fig.7.3b,c), the b<strong>and</strong> becomes flatter. As a consequence,<br />
the quadratic regime disappears <strong>and</strong> the slope of the phononic regime decreases. This reflects<br />
the strong decrease of the velocity of sound as the lattice is made deeper (see discussion below<br />
<strong>in</strong> section 7.4).<br />
In Fig.7.4, we plot the energy gap between lowest <strong>and</strong> first excited b<strong>and</strong> as a function of<br />
lattice depth for gn/ER =1. For comparison, we display the correspond<strong>in</strong>g curve for the<br />
energy gap <strong>in</strong> the Bloch b<strong>and</strong> spectrum of a s<strong>in</strong>gle particle (see Fig.6.6). In addition, we<br />
plot the gap 2 √ sER between the vibrational levels obta<strong>in</strong>ed when approximat<strong>in</strong>g the bottom<br />
of a lattice well by a harmonic potential (see Eq.(6.48)). It turns out that the gap <strong>in</strong> the<br />
Bogoliubov b<strong>and</strong> spectrum approaches the one <strong>in</strong> the s<strong>in</strong>gle particle spectrum as s is tuned to<br />
large values. This is the case because <strong>in</strong> a very deep lattice the first excited b<strong>and</strong> is almost not<br />
affected by <strong>in</strong>teractions <strong>and</strong> is hence essentially given by the s<strong>in</strong>gle particle Bloch b<strong>and</strong> while<br />
the lowest Bogoliubov b<strong>and</strong> becomes so flat that the excitation energy at the zone boundary<br />
is negligibly small compared to the energies of the second b<strong>and</strong>. Note that the convergence to<br />
the gap 2 √ sER of the harmonic approximation is very slow, reflect<strong>in</strong>g ma<strong>in</strong>ly the role of the<br />
anharmonicity of the potential wells.