Linear Programming Lecture Notes - Penn State Personal Web Server

4. Rays and Directions
Recall the definition of a line (Definition 1.10 from Chapter 1. A ray is a one sided line.
Definition 4.18 (Ray). Let x0 ∈ R n be a point and and let d ∈ R n be a vector
called the direction. Then the ray with vertex x0 and direction d is the collection of points
{x|x = x0 + λd, λ ≥ 0}.
Example 4.19. We will use the same point and direction as we did for a line in Chapter
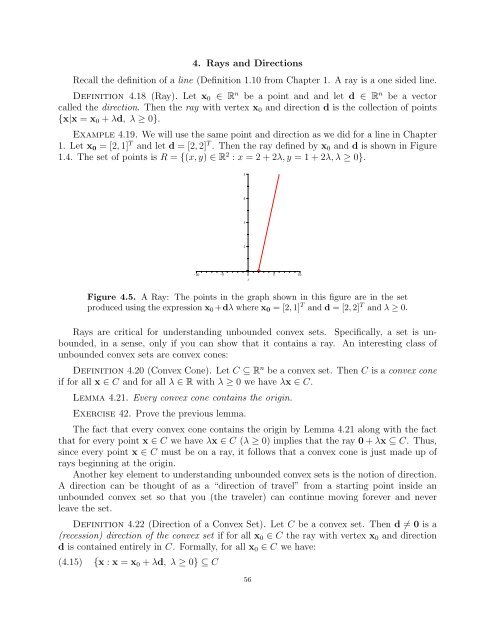
1. Let x0 = [2, 1] T and let d = [2, 2] T . Then the ray defined by x0 and d is shown in Figure
1.4. The set of points is R = {(x, y) ∈ R 2 : x = 2 + 2λ, y = 1 + 2λ, λ ≥ 0}.
Figure 4.5. A Ray: The points in the graph shown in this figure are in the set
produced using the expression x0 +dλ where x0 = [2, 1] T and d = [2, 2] T and λ ≥ 0.
Rays are critical for understanding unbounded convex sets. Specifically, a set is unbounded,
in a sense, only if you can show that it contains a ray. An interesting class of
unbounded convex sets are convex cones:
Definition 4.20 (Convex Cone). Let C ⊆ R n be a convex set. Then C is a convex cone
if for all x ∈ C and for all λ ∈ R with λ ≥ 0 we have λx ∈ C.
Lemma 4.21. Every convex cone contains the origin.
Exercise 42. Prove the previous lemma.
The fact that every convex cone contains the origin by Lemma 4.21 along with the fact
that for every point x ∈ C we have λx ∈ C (λ ≥ 0) implies that the ray 0 + λx ⊆ C. Thus,
since every point x ∈ C must be on a ray, it follows that a convex cone is just made up of
rays beginning at the origin.
Another key element to understanding unbounded convex sets is the notion of direction.
A direction can be thought of as a “direction of travel” from a starting point inside an
unbounded convex set so that you (the traveler) can continue moving forever and never
leave the set.
Definition 4.22 (Direction of a Convex Set). Let C be a convex set. Then d = 0 is a
(recession) direction of the convex set if for all x0 ∈ C the ray with vertex x0 and direction
d is contained entirely in C. Formally, for all x0 ∈ C we have:
(4.15) {x : x = x0 + λd, λ ≥ 0} ⊆ C
56