Linear Programming Lecture Notes - Penn State Personal Web Server

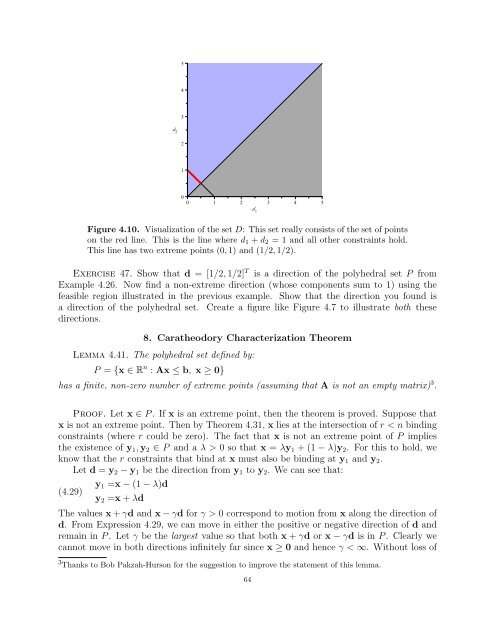
Figure 4.10. Visualization of the set D: This set really consists of the set of points
on the red line. This is the line where d1 + d2 = 1 and all other constraints hold.
This line has two extreme points (0, 1) and (1/2, 1/2).
Exercise 47. Show that d = [1/2, 1/2] T is a direction of the polyhedral set P from
Example 4.26. Now find a non-extreme direction (whose components sum to 1) using the
feasible region illustrated in the previous example. Show that the direction you found is
a direction of the polyhedral set. Create a figure like Figure 4.7 to illustrate both these
directions.
8. Caratheodory Characterization Theorem
Lemma 4.41. The polyhedral set defined by:
P = {x ∈ R n : Ax ≤ b, x ≥ 0}
has a finite, non-zero number of extreme points (assuming that A is not an empty matrix) 3 .
Proof. Let x ∈ P . If x is an extreme point, then the theorem is proved. Suppose that
x is not an extreme point. Then by Theorem 4.31, x lies at the intersection of r < n binding
constraints (where r could be zero). The fact that x is not an extreme point of P implies
the existence of y1, y2 ∈ P and a λ > 0 so that x = λy1 + (1 − λ)y2. For this to hold, we
know that the r constraints that bind at x must also be binding at y1 and y2.
Let d = y2 − y1 be the direction from y1 to y2. We can see that:
(4.29)
y1 =x − (1 − λ)d
y2 =x + λd
The values x + γd and x − γd for γ > 0 correspond to motion from x along the direction of
d. From Expression 4.29, we can move in either the positive or negative direction of d and
remain in P . Let γ be the largest value so that both x + γd or x − γd is in P . Clearly we
cannot move in both directions infinitely far since x ≥ 0 and hence γ < ∞. Without loss of
3 Thanks to Bob Pakzah-Hurson for the suggestion to improve the statement of this lemma.
64