DIFFERENTIAL GEOMETRY: A First Course in Curves and Surfaces

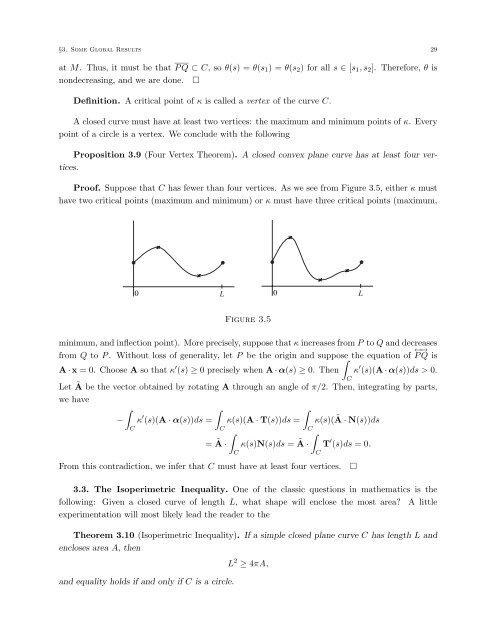
§3. Some Global Results 29at M. Thus, it must be that PQ ⊂ C, soθ(s) =θ(s 1 )=θ(s 2 ) for all s ∈ [s 1 ,s 2 ]. Therefore, θ isnondecreasing, and we are done. □Definition. A critical point of κ is called a vertex of the curve C.A closed curve must have at least two vertices: the maximum and minimum points of κ. Everypoint of a circle is a vertex. We conclude with the followingProposition 3.9 (Four Vertex Theorem). A closed convex plane curve has at least four vertices.Proof. Suppose that C has fewer than four vertices. As we see from Figure 3.5, either κ musthave two critical points (maximum and minimum) or κ must have three critical points (maximum,0 L 0 LFigure 3.5minimum, and inflection point). More precisely, suppose that κ increases from P to Q and decreasesfrom Q to P . Without loss of generality, let P be the origin and suppose ∫ the equation of PQ ←→ isA · x =0. Choose A so that κ ′ (s) ≥ 0 precisely when A · α(s) ≥ 0. Then κ ′ (s)(A · α(s))ds > 0.Let à be the vector obtained by rotating A through an angle of π/2. Then, integrating by parts,we have∫∫∫− κ ′ (s)(A · α(s))ds = κ(s)(A · T(s))ds = κ(s)(à · N(s))dsCCC∫∫= à · κ(s)N(s)ds = à · T ′ (s)ds =0.From this contradiction, we infer that C must have at least four vertices.C3.3. The Isoperimetric Inequality. One of the classic questions in mathematics is thefollowing: Given a closed curve of length L, what shape will enclose the most area? A littleexperimentation will most likely lead the reader to theTheorem 3.10 (Isoperimetric Inequality). If a simple closed plane curve C has length L andencloses area A, thenand equality holds if and only if C is a circle.L 2 ≥ 4πA,CC□