Transformada de Fourier

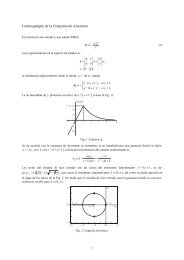
2.3. La transformada de Fourier 91Esta integral se puede calcular como la integral de contornoZ1z e−j2π f z dz,Cdonde el contorno de integración C es el borde del semidisco de radio R con una pequeña indentaciónde radio ε en el origen, donde R se hace tender a infinito, y ε a cero. Bajo estas condiciones, laintegral coincide con la transformada que se desea calcular si Im{z} = 0. En este caso, la funciónf (z) = 1/z tiene un polo en el eje real, en z = 0.El semiplano donde yace C se elige de modo que el integrando tienda a cero cuando R → ∞, yesto impone condiciones sobre f , de manera de satisfacer las condiciones de los lemas de Jordan. Encualquier caso la región de integración debe elegirse de modo que e −j2π f z → 0 cuando R → ∞.Si f > 0, esta región está dada por Im{z} < 0, y si f < 0, la región de analiticidad es Im{z} > 0.Para una curva C contenida en la región Im{z} > 0, que corresponde a f < 0, donde C estáformada por la unión de las curvas γ R = R e jθ , 0 ≤ θ ≤ π, el segmento de recta [−R, −ε], la curvaγ ε = εe jθ , con −π ≤ θ ≤ 0, y el segmento de recta [ε, R], como se muestra en Fig. 2.16(a) , laintegral de contorno es nula porque la curva no encierra ningún polo. Se tiene entonces queZ0 =C1z e−j2π f z dz =Z −ε−RZ Rε1t e−j2π f t dt +1t e−j2π f t dt +ZZγ ε1z e−j2π f z dz +γ R1z e−j2π f z dz,donde se efectuó el cambio de variable z ↦→ t = Re{z} sobre las rectas.Sobre la curva γ R se hace la sustitución z ↦→ Re jθ , dz = jRe jθ dθ, resultandoZZ1πZγ Rz e−j2π f z 1πdz =0 R e jθ e−j2π f (R ejθ) jR e jθ dθ = j e −j2π f R(cos θ+j sen θ) dθ.0Teniendo en cuenta quelímR→+∞e −j2π f R(cos θ+j sen θ) =límR→+∞e f R sen θ Como para esta región sen θ ≥ 0, la única manera que el integrando se anule para R → ∞ es quef < 0. Entonces,Z1límR→0 γ Rz e−j2π f z dz = 0 para f < 0.Sobre la curva γ ε se tiene que z = εe jθ , dz = jεe jθ dθ, y por lo tanto,ZZ10Zγ εz e−j2π f z 10dz =−π εe jθ e−j2π f (εejθ) jεe jθ (−dθ) = −j e −j2π f ε(cos θ+j sen θ) dθ.−πEl signo del dθ tiene en cuenta que la curva γ ε está orientada en sentido horario. Cuando ε → 0, elargumento de la integral tiende a 1, y entoncesZ1límε→0 γ εz e−j2π f z dz = −jπ.A partir de estos resultados se encuentra que Z −εZ1∞0 = límε→0 −∞ t e−j2π f t 1dt +ε t e−j2π f t dt − jπ,| {z }X( f )de modo queX( f ) = jπ si f < 0.Si f > 0, el contorno de integración que se elige es el que se representa en la Fig. 2.16(b) . Eldesarrollo es idéntico, con un par de salvedades:Procesamiento Digital de Señales U.N.S. 2011