Transformada de Fourier

More documents

Recommendations

Info

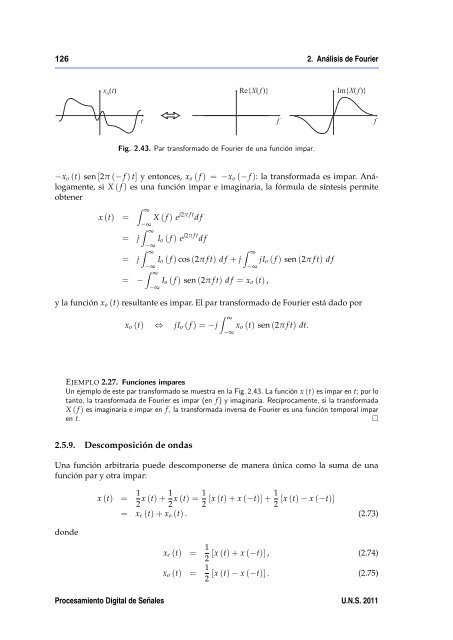
2.5. Propiedades de la transformada de Fourier 125Fig. 2.42. Par transformado de Fourier de una función par.El par transformado se obtiene de manera trivial:X ( f ) ===Z ∞−∞Z ∞−∞Z ∞−∞x (t) e −j2π f t dtx e (t) cos (2π f t) dt − jZ ∞−∞x e (t) cos (2π f t) dt = R e ( f ) .x e (t) sen (2π f t) dtLa parte imaginaria se anula ya que el integrando es una función impar. Como cos (2π f t)es una función par, x e (t) cos (2π f t) = x e (t) cos [2π (− f ) t] y entonces, X e ( f ) = X e (− f ):la transformada es par. De manera similar, si X ( f ) es una función real y par de la frecuencia,la fórmula de síntesis permite obtenerx (t) ===Z ∞−∞Z ∞−∞Z ∞−∞X e ( f ) e j2π f t d f =Z ∞−∞R e ( f ) cos (2π f t) d f + jR e ( f ) e j2π f t d fZ ∞−∞R e ( f ) cos (2π f t) d f = x e (t) .R e ( f ) sen (2π f t) d fEJEMPLO 2.26. Funciones paresComo se muestra en la Fig. 2.42, la transformada de Fourier de una función par es una función realy par de la frecuencia; recíprocamente, la transformada inversa de Fourier de una función real y parde la frecuencia es una función par del tiempo.2.5.8. Funciones imparesSi x o (t) = −x o (−t), entonces x o (t) es una función impar del tiempo, y su transformadade Fourier es una función impar e imaginaria:X ( f ) ==Z ∞−∞Z ∞= −j−∞Z ∞x o (t) e −j2π f t dtx o (t) cos (2π f t) dt − j−∞Z ∞−∞x o (t) sen (2π f t) dt = jI o ( f ) .x o (t) sen (2π f t) dtEl integrando real es nulo ya que la multiplicación de una función par por una impares una función impar. Como sen (2π f t) es una función impar, x o (t) sen (2π f t) =Procesamiento Digital de Señales U.N.S. 2011
126 2. Análisis de FourierFig. 2.43. Par transformado de Fourier de una función impar.−x o (t) sen [2π (− f ) t] y entonces, x o ( f ) = −x o (− f ): la transformada es impar. Análogamente,si X ( f ) es una función impar e imaginaria, la fórmula de síntesis permiteobtenerx (t) == j= jZ ∞= −−∞Z ∞−∞Z ∞−∞Z ∞X ( f ) e j2π f t d f−∞I o ( f ) e j2π f t d fI o ( f ) cos (2π f t) d f + jZ ∞−∞I o ( f ) sen (2π f t) d f = x o (t) ,jI o ( f ) sen (2π f t) d fy la función x o (t) resultante es impar. El par transformado de Fourier está dado porZ ∞x o (t) ⇔ jI o ( f ) = −j x o (t) sen (2π f t) dt.−∞EJEMPLO 2.27. Funciones imparesUn ejemplo de este par transformado se muestra en la Fig. 2.43. La función x (t) es impar en t; por lotanto, la transformada de Fourier es impar (en f ) y imaginaria. Recíprocamente, si la transformadaX ( f ) es imaginaria e impar en f , la transformada inversa de Fourier es una función temporal imparen t.2.5.9. Descomposición de ondasUna función arbitraria puede descomponerse de manera única como la suma de unafunción par y otra impar:dondex (t) = 1 2 x (t) + 1 2 x (t) = 1 2 [x (t) + x (−t)] + 1 [x (t) − x (−t)]2= x e (t) + x o (t) . (2.73)x e (t) = 1 [x (t) + x (−t)] , (2.74)2x o (t) = 1 [x (t) − x (−t)] . (2.75)2Procesamiento Digital de Señales U.N.S. 2011
Page 1 and 2: 82 2. Análisis de FourierFig. 2.9.
Page 3 and 4: 84 2. Análisis de FourierFig. 2.11
Page 13 and 14: 94 2. Análisis de Fourierfunción
Page 25: 106 2. Análisis de FourierHaciendo
Page 28 and 29: 2.4. Señales periódicas y la tran
Page 36 and 37: 2.5. Propiedades de la transformada

Transformada de Fourier

Create successful ePaper yourself

Delete template?

Save as template?