Capítulo 3: APLICACIONES DE LAS DERIVADAS

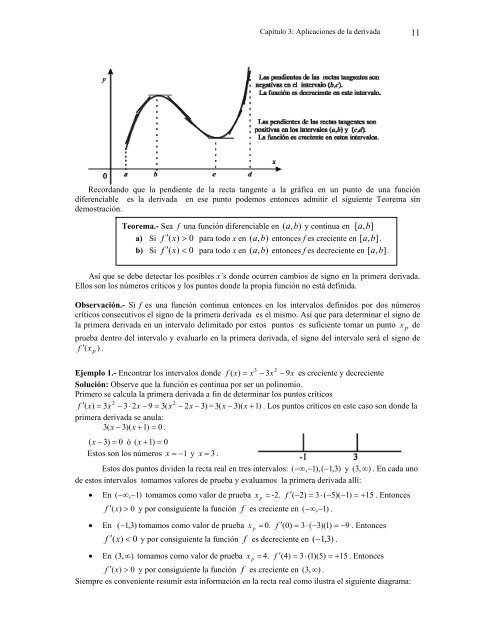
Capítulo 3: Aplicaciones de la derivada 11Recordando que la pendiente de la recta tangente a la gráfica en un punto de una funcióndiferenciable es la derivada en ese punto podemos entonces admitir el siguiente Teorema sindemostración.Teorema.- Sea f una función diferenciable en ( a , b)y continua en [ a , b]a) Si f ( x) 0 para todo x en ( a , b)entonces f es creciente en [ a , b].b) Si f ( x) 0 para todo x en ( a , b)entonces f es decreciente en [ a , b].Así que se debe detectar los posibles x´s donde ocurren cambios de signo en la primera derivada.Ellos son los números críticos y los puntos donde la propia función no está definida.Observación.- Si f es una función continua entonces en los intervalos definidos por dos númeroscríticos consecutivos el signo de la primera derivada es el mismo. Así que para determinar el signo dela primera derivada en un intervalo delimitado por estos puntos es suficiente tomar un punto x p deprueba dentro del intervalo y evaluarlo en la primera derivada, el signo del intervalo será el signo def ( x p ) .Ejemplo 1.- Encontrar los intervalos donde f ( x) x 3x 9xes creciente y decrecienteSolución: Observe que la función es continua por ser un polinomio.Primero se calcula la primera derivada a fin de determinar los puntos críticos22f (x) 3x 32x 9 3( x 2x 3) = 3(x 3)( x 1). Los puntos críticos en este caso son donde laprimera derivada se anula:3(x 3)( x 1) 0 .( x 3) 0 ó ( x 1) 0Estos son los números x 1y x 3 .Estos dos puntos dividen la recta real en tres intervalos: ( , 1),(1,3)y ( 3, ) . En cada unode estos intervalos tomamos valores de prueba y evaluamos la primera derivada allí: En ( , 1)tomamos como valor de prueba x p -2. f ( 2) 3( 5)(1) 15. Entoncesf ( x) 0 y por consiguiente la función f es creciente en ( , 1). En (1,3)tomamos como valor de prueba x 0. f ( 0) 3( 3)(1) 9f ( x) 0 y por consiguiente la función f es decreciente en ( 1,3).p32. Entonces En ( 3, ) tomamos como valor de prueba x p 4. f ( 4) 3(1)(5) 15. Entoncesf ( x) 0 y por consiguiente la función f es creciente en ( 3, ) .Siempre es conveniente resumir esta información en la recta real como ilustra el siguiente diagrama: