Молодой учёный

“Young Scientist” . #3 (50) . March 2013 Technical Sciences
тодов удаётся установить аналитическую связь параметров
прочности, жесткости и устойчивости от отдельных
геометрических характеристик конструкций и физико-механических
свойств материала. Это способствует более
правильному представлению о силовых схемах в исследуемых
конструкциях. Одним из таких методов расчета
плитных конструкций является метод интерполяции по
коэффициенту формы (МИКФ) [2].
В основе МИКФ лежит изопериметрический метод,
основоположниками которого являются Д. Пойа и и Г.
Сеге [1], так как основным аргументом в получаемых аналитических
зависимостях является отношение коэффициента
формы [2;3] к площади области (К f/А). Отличие его
заключается в том, что, если при использовании изопериметрического
метода поведение интегральных параметров
внутри множества решений между опорными не известно,
то при использовании МИКФ получается аналитическая
зависимость, позволяющая найти решение для любой фигуры
из рассматриваемого множества.
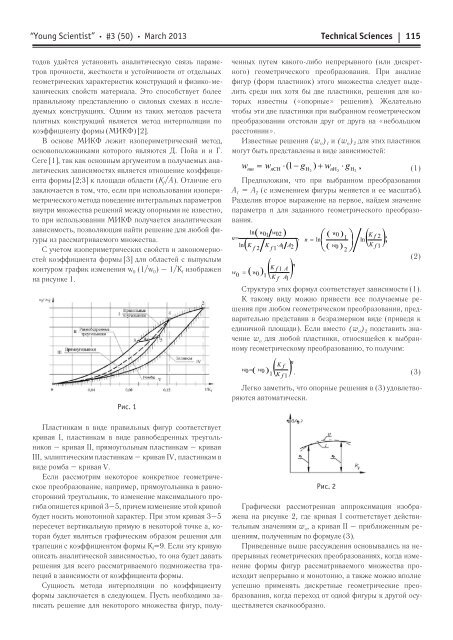
С учетом изопериметрических свойств и закономерностей
коэффициента формы [3] для областей с выпуклым
контуром график изменения w 0 (1/w 0) – 1/K f изображен
на рисунке 1.
Рис. 1
Пластинкам в виде правильных фигур соответствует
кривая I, пластинкам в виде равнобедренных треугольников
– кривая II, прямоугольным пластинкам – кривая
III, эллиптическим пластинкам – кривая IV, пластинкам в
виде ромба – кривая V.
Если рассмотрим некоторое конкретное геометрическое
преобразование, например, прямоугольника в равносторонний
треугольник, то изменение максимального прогиба
опишется кривой 3–5, причем изменение этой кривой
будет носить монотонной характер. При этом кривая 3–5
пересечет вертикальную прямую в некоторой точке а, которая
будет являться графическим образом решения для
трапеции с коэффициентом формы К f=9. Если эту кривую
описать аналитической зависимостью, то она будет давать
решения для всего рассматриваемого подмножества трапеций
в зависимости от коэффициента формы.
Сущность метода интерполяции по коэффициенту
формы заключается в следующем. Пусть необходимо записать
решение для некоторого множества фигур, полу-
115
ченных путем какого-либо непрерывного (или дискретного)
геометрического преобразования. При анализе
фигур (форм пластинок) этого множества следует выделить
среди них хотя бы две пластинки, решения для которых
известны («опорные» решения). Желательно
чтобы эти две пластинки при выбранном геометрическом
преобразовании отстояли друг от друга на «небольшом
расстоянии».
Известные решения (w o) 1 и (w o) 2 для этих пластинок
могут быть представлены в виде зависимостей:
(1)
Предположим, что при выбранном преобразовании
А1 = А2 (с изменением фигуры меняется и ее масштаб).
Разделив второе выражение на первое, найдем значение
параметра n для заданного геометрического преобразования.
Структура этих формул соответствует зависимости (1).
К такому виду можно привести все получаемые решения
при любом геометрическом преобразовании, предварительно
представив в безразмерном виде (приведя к
единичной площади). Если вместо (w o) 2 подставить значение
w o для любой пластинки, относящейся к выбранному
геометрическому преобразованию, то получим:
(2)
. (3)
Легко заметить, что опорные решения в (3) удовлетворяются
автоматически.
Рис. 2
Графически рассмотренная аппроксимация изображена
на рисунке 2, где кривая I соответствует действительным
значениям w o, а кривая II – приближенным решениям,
полученным по формуле (3).
Приведенные выше рассуждения основывались на непрерывных
геометрических преобразованиях, когда изменение
формы фигур рассматриваемого множества происходит
непрерывно и монотонно, а также можно вполне
успешно применять дискретные геометрические преобразования,
когда переход от одной фигуры к другой осуществляется
скачкообразно.