Numerické metody – studijní opora

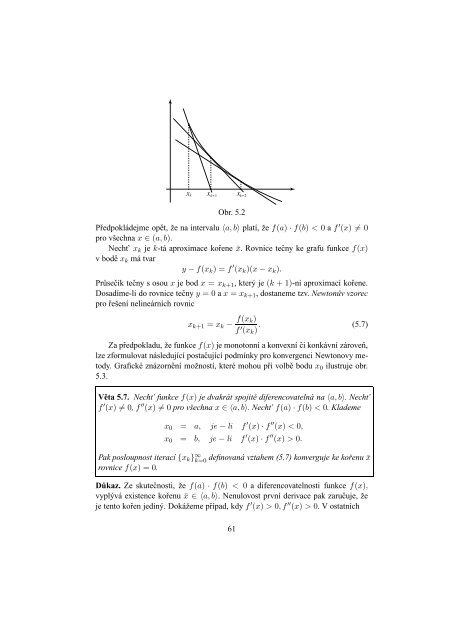
x k x k+1 x k+2Obr. 5.2Předpokládejme opět, že na intervalu 〈a,b〉 platí, že f(a) · f(b) < 0 a f ′ (x) ≠ 0pro všechna x ∈ (a,b).Necht’ x k je k-tá aproximace kořene ¯x. Rovnice tečny ke grafu funkce f(x)v bodě x k má tvary − f(x k ) = f ′ (x k )(x − x k ).Průsečík tečny s osou x je bod x = x k+1 , který je (k + 1)-ní aproximací kořene.Dosadíme-li do rovnice tečny y = 0 a x = x k+1 , dostaneme tzv. Newtonův vzorecpro řešení nelineárních rovnicx k+1 = x k − f(x k)f ′ (x k ) . (5.7)Za předpokladu, že funkce f(x) je monotonní a konvexní či konkávní zároveň,lze zformulovat následující postačující podmínky pro konvergenci Newtonovy metody.Grafické znázornění možností, které mohou při volbě bodu x 0 ilustruje obr.5.3.Věta 5.7. Necht’ funkce f(x) je dvakrát spojitě diferencovatelná na 〈a,b〉. Necht’f ′ (x) ≠ 0, f ′′ (x) ≠ 0 pro všechna x ∈ 〈a,b〉. Necht’ f(a) · f(b) < 0. Klademex 0 = a, je − li f ′ (x) · f ′′ (x) < 0,x 0 = b, je − li f ′ (x) · f ′′ (x) > 0.Pak posloupnost iterací {x k } ∞ k=0 definovaná vztahem (5.7) konverguje ke kořenu ¯xrovnice f(x) = 0.Důkaz. Ze skutečnosti, že f(a) · f(b) < 0 a diferencovatelnosti funkce f(x),vyplývá existence kořenu ¯x ∈ 〈a,b〉. Nenulovost první derivace pak zaručuje, žeje tento kořen jediný. Dokážeme případ, kdy f ′ (x) > 0,f ′′ (x) > 0. V ostatních61