Løsning til røde vejledende eksamensopgaver - szymanski spil

Løsningerne er hentet på www.szymanskispil.dk Quizspillene: Sportsnørd, Ashram, MIR og Universalnørd
Opgave 11: Det er et uafhængighedstest, der skal anvendes.
Dvs. nulhypotesen må derfor nødvendigvis blive
H0: Børns rygevaner er uafhængige af forældres rygevaner.
Dette giver dog en slags problem i forhold til opgavens konklusion, fordi opgaven er formuleret
på en måde, så den kun kan besvares, hvis nulhypotesen forkastes (se nedenfor).
Nulhypotesen undersøges ved et 2 -uafhængighedstest ved på TI n’spire at indtaste:
3533 chi22 way : stat. results
23 46
, der giver:
2
4,6149457
pval
0,031693,2% df 1
Signifikansniveauet er sat til 5%, og da p-værdien er under 5%, må nulhypotesen altså forkastes.
Dvs. der er IKKE belæg for at hævde, at børns rygevaner er uafhængige af forældres rygevaner.
Da der er én frihedsgrad, og da man arbejder med signifikansniveauet 5%, kunne man også være
kommet frem til konklusionen ud fra 2 -værdien, der skal sammenlignes med 3,84, og da den er
større end denne, må nulhypotesen forkastes.
Problemet med opgaveformuleringen er, at man i det tilfælde, hvor nulhypotesen ikke var blevet
forkastet, skulle have konkluderet, at der ikke var belæg for at hævde, at børns rygevaner ikke er
uafhængige af forældres rygevaner, og det ville i så fald ikke have været et svar på opgaven.
Opgave 12: a) Man kender to sider og en vinkel, der ikke dannes af de to sider, så man skal bruge
sinusrelationer til at bestemme vinkel A i trekant ABC:
sin A sin C sin C
sin Aa a c c
Da vinkel A ses at være spids, har man:
1
sin 60
A sin 2,7 76,9767188198
2,4
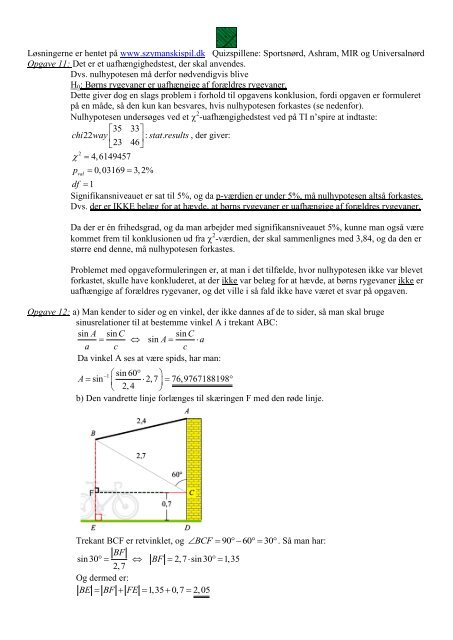
b) Den vandrette linje forlænges til skæringen F med den røde linje.
Trekant BCF er retvinklet, og BCF 90 60 30.
Så man har:
BF
sin30
2,7
Og dermed er:
BF 2,7 sin30 1,35
BE BF FE 1,35 0,7
2,05