Über Familien sphärisch symmetrischer stationärer Lösungen des ...

1 Vorbereitungen
Nachdem wir nun einen Lösungsbegriff definiert haben, der zu stationären
Lösungen führt, die im Allgemeinen nicht als Daten des klassischen Anfangswertproblems
dienen können, aber eventuell dennoch unseren Anforderungen
an ein physikalisches Modell genügen, stellt sich aus mathematischer Sicht die
Frage, welchen Mindestanforderungen die Ansatzfunktionen genügen müssen,
so dass weiterhin Lösungen mit gewissen Eigenschaften existieren. Im letzten
Kapitel werden wir uns noch einmal mit dieser Thematik beschäftigen.
Im Bezug auf den soeben definierten Lösungsbegriff 1.6 finden wir zusammenfassend
die folgende Situation vor: Gegeben eine feste Ansatzfunktion wie in
(1.11) und (1.12) existiert zu jedem Anfangswert y 0 für das Potential eine eindeutig
bestimmte Lösung der Gleichung (1.29). In diesem Fall heißt (f,U) wie
in (1.32) und (1.33) eine sphärisch symmetrische stationäre Lösung des VPS
vom Typ . Die Familien der Lösungen zu festen Ansatzfunktionen und insbesondere
die dort auftretenden Masse-Radius-Kombinationen bilden das zentrale
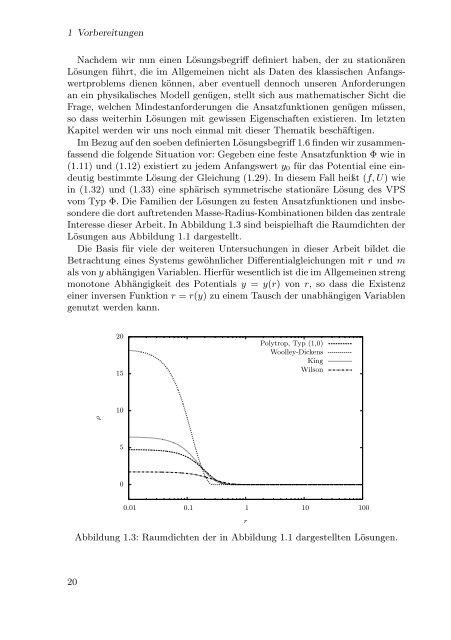
Interesse dieser Arbeit. In Abbildung 1.3 sind beispielhaft die Raumdichten der
Lösungen aus Abbildung 1.1 dargestellt.
Die Basis für viele der weiteren Untersuchungen in dieser Arbeit bildet die
Betrachtung eines Systems gewöhnlicher Differentialgleichungen mit r und m
als von y abhängigen Variablen. Hierfür wesentlich ist die im Allgemeinen streng
monotone Abhängigkeit des Potentials y = y(r) von r, sodassdieExistenz
einer inversen Funktion r = r(y) zu einem Tausch der unabhängigen Variablen
genutzt werden kann.
20
15
Polytrop, Typ (1,0)
Woolley-Dickens
King
Wilson
10
⇢
5
0
0.01 0.1 1 10 100
Abbildung 1.3: Raumdichten der in Abbildung 1.1 dargestellten Lösungen.
r
20