Set of supplementary notes.

10.3. TOTAL ENERGY EXPANSION FOR LANDAU FERMI LIQUID 149
Energy
N=4
N=4
N=3
N=2
N=1
N=0
0 1
N=3
N=2
N=1
N=0
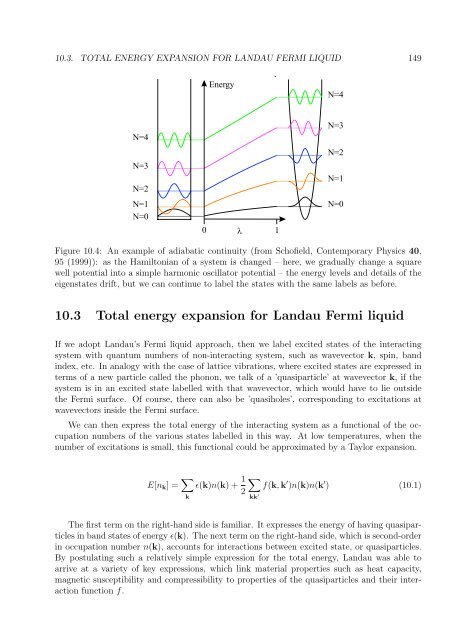
Figure 10.4: An example of adiabatic continuity (from Schofield, Contemporary Physics 40,
95 (1999)): as the Hamiltonian of a system is changed – here, we gradually change a square
well potential into a simple harmonic oscillator potential – the energy levels and details of the
eigenstates drift, but we can continue to label the states with the same labels as before.
10.3 Total energy expansion for Landau Fermi liquid
If we adopt Landau’s Fermi liquid approach, then we label excited states of the interacting
system with quantum numbers of non-interacting system, such as wavevector k, spin, band
index, etc. In analogy with the case of lattice vibrations, where excited states are expressed in
terms of a new particle called the phonon, we talk of a ’quasiparticle’ at wavevector k, if the
system is in an excited state labelled with that wavevector, which would have to lie outside
the Fermi surface. Of course, there can also be ’quasiholes’, corresponding to excitations at
wavevectors inside the Fermi surface.
We can then express the total energy of the interacting system as a functional of the occupation
numbers of the various states labelled in this way. At low temperatures, when the
number of excitations is small, this functional could be approximated by a Taylor expansion.
E[n k ] = ∑ k
ɛ(k)n(k) + 1 2
∑
kk ′ f(k, k ′ )n(k)n(k ′ ) (10.1)
The first term on the right-hand side is familiar. It expresses the energy of having quasiparticles
in band states of energy ɛ(k). The next term on the right-hand side, which is second-order
in occupation number n(k), accounts for interactions between excited state, or quasiparticles.
By postulating such a relatively simple expression for the total energy, Landau was able to
arrive at a variety of key expressions, which link material properties such as heat capacity,
magnetic susceptibility and compressibility to properties of the quasiparticles and their interaction
function f.