Set of supplementary notes.

More documents

Recommendations

Info

152 CHAPTER 10. FERMI LIQUID THEORY will evolve in time following the Schrödinger prescription ψ k (r, t) = ψ k (r)e −iɛ kt/h¯ . (10.3) Here ψ k is the Bloch wavefunction satisfying the time-independent Schrödinger equation, and the time-dependent solution oscillates in time with a single frequency, given by h¯ω = ɛ k , the band energy. If we look at this in Fourier space, we should say that ψ k (r, ω) = 2πψ k (r)δ(ω − ɛ k ) (10.4) so that the wavefunction has spectral weight only at ω = ɛ k /h¯. 1 We can say that the probability amplitude of finding an electronic state with energy ω and momentum k is just A(k, ω) = δ(ω − ɛ k ) , (10.5) where the quantity A(k, ω) is usually called the electron spectral function. What about an interacting system In this case, (i) interactions modify the precise form of the dispersion relation, so we should replace ɛ k by a renormalised ˜ɛ k . This latter is often referred to as a mass renormalisation: m ∗ /m = ɛ k / ˜ɛ k . Moreover, (ii), if we add a quasiparticle, it will scatter from other quasiparticles or by creating particle-hole pairs. Because of this, the probability amplitude of finding a quasiparticle of momentum k at time t will decay exponentially at a rate given by the quasiparticle scattering rate Γ k . These two effects change the time-dependence of the state to e (iɛ k/h¯−Γ k )t and after a Fourier transform lead to an ansatz for the spectral function in an interacting system of the form A(k, ω) = − 1 [ ] π I 1 (10.6) ω − ˜ɛ k /h¯ + iΓ(k) Notice that if the inverse lifetime Γ k → 0, the spectral function reduces to the noninteracting (10.5). (10.6) describes quasiparticles with a dispersion curve ˜ɛ k and a decay rate (inverse lifetime) Γ k . We must be careful about the chemical potential. If we are in equilibrium (and at T=0), we cannot add fermionic excitation at an energy ω < µ. So we shall infer that for ω > µ, (10.6) is the spectral function for particle-like excitations, whereas for ω < µ it is the spectral function for holes. If Γ k is small, then the quasiparticles are long-lived and have some real meaning. More precisely: a quasiparticle resonance at energy h¯ω = ˜ɛ k can be resolved, if the peak width in the spectral function is less than the peak’s centre position, or, borrowing the terminology developed for damped harmonic oscillators, if the quality factor (ratio of peak position over peak width) is larger than 1. For an interacting system (right panel in Fig. 10.7), A has width = 2 × Γ k . The phase-space argument made in section 10.3.1 showed that Γ k ∝ ɛ 2 . The quality factor ˜ɛ k /Γ ∝ ˜ɛ k /˜ɛ 2 k therefore diverges for ɛ → 0. We find that quasiparticles are overdamped at high energies, but well-defined for E → E F . 1 Getting the sign here requires one to adopt a sign convention for Fourier transforms that is opposite to the one often used in maths books. We have also set h¯ = 1.
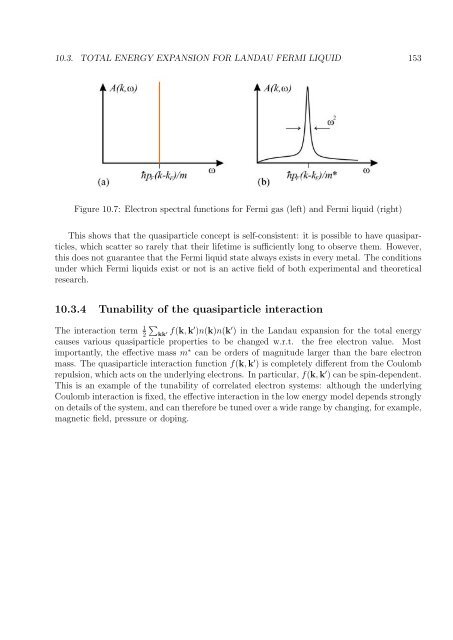
10.3. TOTAL ENERGY EXPANSION FOR LANDAU FERMI LIQUID 153 Figure 10.7: Electron spectral functions for Fermi gas (left) and Fermi liquid (right) This shows that the quasiparticle concept is self-consistent: it is possible to have quasiparticles, which scatter so rarely that their lifetime is sufficiently long to observe them. However, this does not guarantee that the Fermi liquid state always exists in every metal. The conditions under which Fermi liquids exist or not is an active field of both experimental and theoretical research. 10.3.4 Tunability of the quasiparticle interaction ∑ The interaction term 1 2 kk f(k, k ′ )n(k)n(k ′ ) in the Landau expansion for the total energy ′ causes various quasiparticle properties to be changed w.r.t. the free electron value. Most importantly, the effective mass m ∗ can be orders of magnitude larger than the bare electron mass. The quasiparticle interaction function f(k, k ′ ) is completely different from the Coulomb repulsion, which acts on the underlying electrons. In particular, f(k, k ′ ) can be spin-dependent. This is an example of the tunability of correlated electron systems: although the underlying Coulomb interaction is fixed, the effective interaction in the low energy model depends strongly on details of the system, and can therefore be tuned over a wide range by changing, for example, magnetic field, pressure or doping.
Page 1:
Quantum Condensed Matter Physics Pa
Page 4 and 5:
4 CONTENTS 5.1 Bands and Brillouin
Page 6 and 7:
6 CONTENTS also serves to give impo
Page 8 and 9:
8 CONTENTS
Page 10 and 11:
10 CHAPTER 1. CLASSICAL MODELS FOR
Page 12 and 13:
Page 14 and 15:
Page 16 and 17:
Page 18 and 19:
Page 20 and 21:
Page 22 and 23:
Page 24 and 25:
24 CHAPTER 2. SOMMERFELD THEORY Fig
Page 26 and 27:
26 CHAPTER 2. SOMMERFELD THEORY 2.4
Page 28 and 29:
28 CHAPTER 2. SOMMERFELD THEORY Res
Page 30 and 31:
30 CHAPTER 2. SOMMERFELD THEORY Thi
Page 32 and 33:
32 CHAPTER 2. SOMMERFELD THEORY
Page 34 and 35:
34 CHAPTER 3. FROM ATOMS TO SOLIDS
Page 36 and 37:
Page 38 and 39:
Page 40 and 41:
Page 42 and 43:
Page 44 and 45:
Page 46 and 47:
Page 48 and 49:
Page 50 and 51:
Page 52 and 53:
Page 54 and 55:
Page 56 and 57:
56 CHAPTER 4. ELECTRONIC STRUCTURE
Page 58 and 59:
Page 60 and 61:
Page 62 and 63:
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
Page 74 and 75:
74 CHAPTER 5. BANDSTRUCTURE OF REAL
Page 76 and 77:
Page 78 and 79:
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 88 and 89:
88 CHAPTER 6. EXPERIMENTAL PROBES O
Page 90 and 91:
Page 92 and 93:
Page 94 and 95:
Page 96 and 97:
Page 98 and 99:
Page 100 and 101:
100 CHAPTER 7. SEMICONDUCTORS Figur
Page 102 and 103: 102 CHAPTER 7. SEMICONDUCTORS is fo
Page 104 and 105: 104 CHAPTER 7. SEMICONDUCTORS Figur
Page 106 and 107: 106 CHAPTER 8. SEMICONDUCTOR DEVICE
Page 116 and 117: ecessitates variances in circuit th
Page 118 and 119: nc... Freescale Semiconductor, I
Page 124 and 125: 124 CHAPTER 9. ELECTRONIC INSTABILI
Page 146 and 147: 146 CHAPTER 10. FERMI LIQUID THEORY
Page 158: 158 CHAPTER 10. FERMI LIQUID THEORY
show all

Set of supplementary notes.

Create successful ePaper yourself

Delete template?

Save as template?