Set of supplementary notes.

62 CHAPTER 4. ELECTRONIC STRUCTURE
E
(0)
|k−G>
G
|k>
−2 π / a − π / a 0 π/ a 2 π/ a
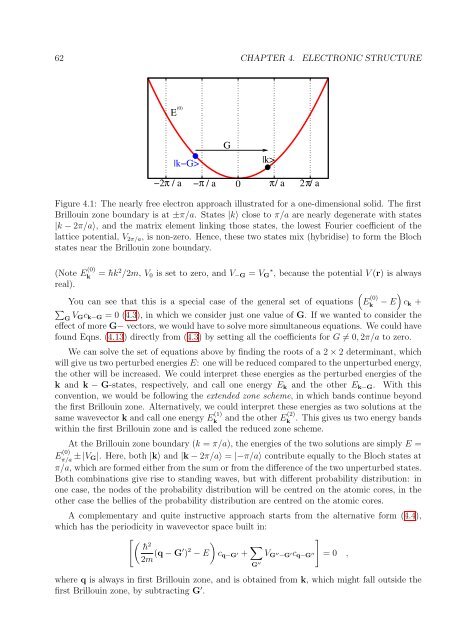
Figure 4.1: The nearly free electron approach illustrated for a one-dimensional solid. The first
Brillouin zone boundary is at ±π/a. States |k〉 close to π/a are nearly degenerate with states
|k − 2π/a〉, and the matrix element linking those states, the lowest Fourier coefficient of the
lattice potential, V 2π/a , is non-zero. Hence, these two states mix (hybridise) to form the Bloch
states near the Brillouin zone boundary.
(Note E (0)
k
real).
= h¯k 2 /2m, V 0 is set to zero, and V −G = V G ∗ , because the potential V (r) is always
(
E (0)
k − E )
c k +
You can see that this is a special case of the general set of equations
∑
G V Gc k−G = 0 (4.3), in which we consider just one value of G. If we wanted to consider the
effect of more G− vectors, we would have to solve more simultaneous equations. We could have
found Eqns. (4.13) directly from (4.3) by setting all the coefficients for G ≠ 0, 2π/a to zero.
We can solve the set of equations above by finding the roots of a 2 × 2 determinant, which
will give us two perturbed energies E: one will be reduced compared to the unperturbed energy,
the other will be increased. We could interpret these energies as the perturbed energies of the
k and k − G-states, respectively, and call one energy E k and the other E k−G . With this
convention, we would be following the extended zone scheme, in which bands continue beyond
the first Brillouin zone. Alternatively, we could interpret these energies as two solutions at the
same wavevector k and call one energy E (1)
k
and the other E(2)
k
. This gives us two energy bands
within the first Brillouin zone and is called the reduced zone scheme.
At the Brillouin zone boundary (k = π/a), the energies of the two solutions are simply E =
E (0)
π/a ± |V G|. Here, both |k〉 and |k − 2π/a〉 = |−π/a〉 contribute equally to the Bloch states at
π/a, which are formed either from the sum or from the difference of the two unperturbed states.
Both combinations give rise to standing waves, but with different probability distribution: in
one case, the nodes of the probability distribution will be centred on the atomic cores, in the
other case the bellies of the probability distribution are centred on the atomic cores.
A complementary and quite instructive approach starts from the alternative form (4.4),
which has the periodicity in wavevector space built in:
[ ( ) h¯ 2
2m (q − G′ ) 2 − E c q−G ′ + ∑ ]
V G ′′ −G ′c q−G ′′ = 0 ,
G ′′
where q is always in first Brillouin zone, and is obtained from k, which might fall outside the
first Brillouin zone, by subtracting G ′ .