Precipitation-Runoff and Streamflow-Routing Models for the ...

More documents

Recommendations

Info

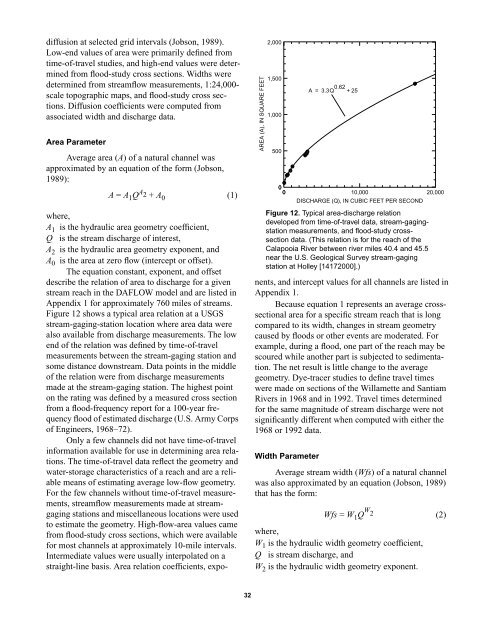
diffusion at selected grid intervals (Jobson, 1989).Low-end values of area were primarily defined fromtime-of-travel studies, and high-end values were determinedfrom flood-study cross sections. Widths weredetermined from streamflow measurements, 1:24,000-scale topographic maps, and flood-study cross sections.Diffusion coefficients were computed fromassociated width and discharge data.Area ParameterAverage area (A) of a natural channel wasapproximated by an equation of the form (Jobson,1989):A = A 1 Q A 2 + A 0 (1)AREA (A), IN SQUARE FEET2,0001,5001,00050000 10,00020,000where,A 1 is the hydraulic area geometry coefficient,Q is the stream discharge of interest,A 2 is the hydraulic area geometry exponent, andA 0 is the area at zero flow (intercept or offset).The equation constant, exponent, and offsetdescribe the relation of area to discharge for a givenstream reach in the DAFLOW model and are listed inAppendix 1 for approximately 760 miles of streams.Figure 12 shows a typical area relation at a USGSstream-gaging-station location where area data werealso available from discharge measurements. The lowend of the relation was defined by time-of-travelmeasurements between the stream-gaging station andsome distance downstream. Data points in the middleof the relation were from discharge measurementsmade at the stream-gaging station. The highest pointon the rating was defined by a measured cross sectionfrom a flood-frequency report for a 100-year frequencyflood of estimated discharge (U.S. Army Corpsof Engineers, 1968–72).Only a few channels did not have time-of-travelinformation available for use in determining area relations.The time-of-travel data reflect the geometry andwater-storage characteristics of a reach and are a reliablemeans of estimating average low-flow geometry.For the few channels without time-of-travel measurements,streamflow measurements made at streamgagingstations and miscellaneous locations were usedto estimate the geometry. High-flow-area values camefrom flood-study cross sections, which were availablefor most channels at approximately 10-mile intervals.Intermediate values were usually interpolated on astraight-line basis. Area relation coefficients, exponents,and intercept values for all channels are listed inAppendix 1.Because equation 1 represents an average crosssectionalarea for a specific stream reach that is longcompared to its width, changes in stream geometrycaused by floods or other events are moderated. Forexample, during a flood, one part of the reach may bescoured while another part is subjected to sedimentation.The net result is little change to the averagegeometry. Dye-tracer studies to define travel timeswere made on sections of the Willamette and SantiamRivers in 1968 and in 1992. Travel times determinedfor the same magnitude of stream discharge were notsignificantly different when computed with either the1968 or 1992 data.Width ParameterA = 3.3Q 0.62 + 25DISCHARGE (Q), IN CUBIC FEET PER SECONDFigure 12. Typical area-discharge relationdeveloped from time-of-travel data, stream-gagingstationmeasurements, and flood-study crosssectiondata. (This relation is for the reach of theCalapooia River between river miles 40.4 and 45.5near the U.S. Geological Survey stream-gagingstation at Holley [14172000].)Average stream width (Wfs) of a natural channelwas also approximated by an equation (Jobson, 1989)that has the form:Wfs = W 1 Q W 2 (2)where,W 1 is the hydraulic width geometry coefficient,Q is stream discharge, andW 2 is the hydraulic width geometry exponent.32
Low-flow width was primarily scaled from1:24,000 topographic maps or higher resolution arealphotography. Both map and photographic informationwere tagged with a date of flight, and the correspondingstream discharge was obtained from USGSstreamflow records. All high-flow widths came fromflood-study cross sections. Missing data were approximatedby interpolation and extrapolation. Width-relationcoefficients and exponents for all channels are inAppendix 1.Diffusion CoefficientsValues for the diffusion coefficient (D f ) wereobtained from the channel slope (S 0 ), discharge (Q)ofinterest, and average width (equation 2) by using thefollowing equation by Doyle and others (1983):D f = Q/2S 0 W (3)Time-of-Travel StudiesDiffusion coefficients for specified high and lowflows are in Appendix 1. Slope as shown in Appendix1 was determined from either topographic maps orfrom U.S. Army Corps of Engineers (1968–72) floodplaininformation.Special Studies to Document Low FlowLow-streamflow data were needed at criticallocations to calibrate low-flow model parameters andto relate streamflow to physical properties of the basin.Time-of-travel studies using dye tracers and low-flowmeasurements to define ground-water gains and losseswere made during the study to identify model lowflowparameters and to better understand the low-flowsystem (fig. 13).Time-of-Travel StudiesIn the time-of-travel studies, rhodamine WT dyewas injected at a selected location in a stream, andGain-Loss Studies1992-93 studies(Lee, 1995)1968 studies(Harris, 1968)Figure 13. Location of time-of-travel and gain-loss studies, Willamette River Basin, Oregon.33
Page 1: Precipitation-Runoff and Streamflow
Page 4 and 5: U.S. DEPARTMENT OF THE INTERIORBRUC
Page 6 and 7: Determining Travel Time and Dilutio
Page 8 and 9: 2. Stream-gaging stations used to c
Page 10 and 11: Page Intentionally Blank
Page 12 and 13: network-routing models where availa
Page 14 and 15: made on the main stem at base-flow
Page 16 and 17: Figure 1. Willamette River Basin, O
Page 18 and 19: EvapotranspirationINPUTSAirtemperat
Page 20 and 21: Table 1. Climate stations used to c
Page 22 and 23: Table 2. Stream-gaging stations use
Page 24 and 25: Figure 4. Mean annual precipitation
Page 26 and 27: Major Land Use MapHydrologic Soil G
Page 28 and 29: 0.5 mi 2 , created in the merge of
Page 30 and 31: Table 6. Geology and soils matrix o
Page 32 and 33: tion value of the HRU class by the
Page 34 and 35: Table 8. Selected monthly basinwide
Page 36 and 37: Figure 9. Location of Precipitation
Page 38 and 39: Table 11. Statistical analyses of P
Page 40 and 41: flow can become a significant compo
Page 44 and 45: samples were collected at various d
Page 46 and 47: 3,0002,500June 21-30, 1993September
Page 48 and 49: stream network is shown on figure 1
Page 50 and 51: 122˚30´ 15´122˚00´121˚45´Roc
Page 52 and 53: 123˚22´30´´ 123˚15´ 123˚00´
Page 54 and 55: 123˚00´´ 45´30´122˚15´45˚15
Page 56 and 57: YamhillRiver123˚45´ 30´ 15´123
Page 58 and 59: 123˚07´30´´ 123˚00´ 45´ 30´
Page 60 and 61: 123˚07´30´´ 123˚00´ 45´ 30´
Page 62 and 63: 44˚15´14166000122˚07´30´´Will
Page 64 and 65: 122˚15´ 122˚00´121˚52´30´´4
Page 66 and 67: 44˚52´30´´45´122˚15´ 122˚00
Page 68 and 69: observed flow at the Willamette Riv
Page 70 and 71: DAFLOW model, and peak amplitude is
Page 72 and 73: 20DYE CONCENTRATION, IN MICROGRAMS
Page 74 and 75: ARC-INFO and Geographic Information
Page 76 and 77: WILL.WDMData-base file(Observed pre
Page 78 and 79: WILL.WDMData-base fileSWSTATSFreque
Page 80 and 81: Jobson, H.E., 1980, Comment on A ne
Page 82 and 83: Page Intentionally Blank
Page 84 and 85: APPENDIX 1. STREAM GEOMETRY FOR MAI
Page 92 and 93:
APPENDIX 1. STREAM GEOMETRY FOR MAI
Page 94 and 95:
Page 96 and 97:
Page 98 and 99:
Page 100 and 101:
Page 102 and 103:
Page 104 and 105:
Page 106 and 107:
Page 108 and 109:
Page 110 and 111:
APPENDIX 2. ARC MACRO LANGUAGE (AML
Page 112 and 113:
Page 114 and 115:
Page 116 and 117:
Page 118 and 119:
Page 120 and 121:
Page 122 and 123:
APPENDIX 3. DEFINITIONS OF PARAMETE
Page 124 and 125:
APPENDIX 3. DEFINITIONS OF PARAMETE
Page 126 and 127:
APPENDIX 4. MEASUREMENTS USED TO DE
Page 128 and 129:
Page 130 and 131:
Page 132 and 133:
Page 134 and 135:
APPENDIX 5. EXAMPLE PRECIPITATION-R
Page 136 and 137:
APPENDIX 5. EXAMPLE PRECIPITATION-R
Page 138 and 139:
APPENDIX 6. DIFFUSION ANALOGY FLOW
Page 140 and 141:
Page 142 and 143:
Page 144 and 145:
Page 146 and 147:
Page 148 and 149:
Page 150 and 151:
APPENDIX 7. PROGRAMMING STEPS TO IN
Page 152 and 153:
APPENDIX 8. PROGRAMMING STEPS TO DE
Page 154 and 155:
Page 156 and 157:
Page 158 and 159:
Page 160 and 161:
150Climatemaxtempmintempprecipitati
Page 162 and 163:
APPENDIX 10. DIRECTORY TREE AND DES
Page 164 and 165:
Page 166 and 167:
Page 168 and 169:
Page 170 and 171:
Page 172 and 173:
Page 174 and 175:
Page 176 and 177:
Page 178 and 179:
Page 180 and 181:
APPENDIX 11. DIRECTORY TREES AND DE
Page 182 and 183:
APPENDIX 11. DIRECTORY TREES AND DE
Page 184 and 185:
APPENDIX 12. DIRECTORY FOR will.wdm
Page 186 and 187:
Page 188 and 189:
Page 190 and 191:
Page 192 and 193:
Page 194 and 195:
Page 196 and 197:
APPENDIX 13. PROGRAMMING STEPS FOR
Page 198 and 199:
Page 200 and 201:
Page 202 and 203:
APPENDIX 14. INPUT FILES FOR BRANCH
Page 204 and 205:
Page 206 and 207:
show all

Precipitation-Runoff and Streamflow-Routing Models for the ...

Create successful ePaper yourself

Delete template?

Save as template?