OS-C501

Offshore Standard DNV-OS-C501, November 2013
Sec.4 Materials - laminates – Page 73
Table 4-16 Default changes of ply properties with matrix damage
Matrix cracking due to stress
(see failure criteria in Sec.6 [4])
Change ply properties to
(see also [9.2.3])
stress σ 2 transverse to the fibre direction E 2 = ν 12 = 0
shear stress σ 12 G 12 = ν 12 = 0
stress σ 3 transverse to the fibre direction E 3 = ν 31 = 0
shear stress σ 13 G 13 = ν 13 = 0
shear stress σ 23 G 23 = ν 23 = 0
9.2.3 In numerical calculations certain problems may arise, e.g. lack of ability to invert the structural stiffness
matrix, when degraded material properties are set equal to 0. To overcome such problems, one may apply small
values, e.g. 1% of the non-degraded values, instead of 0.
Guidance note:
Stiffness of a composite in compression will be similar to the linear (initial) value even under the presence of damage,
since matrix cracks will close. In tension, the stiffness reduces gradually with the increase of damage.
9.3 Experimental approach
---e-n-d---of---G-u-i-d-a-n-c-e---n-o-t-e---
9.3.1 Instead of the default values given in [9.2], gradual degradation of the material properties at ply levels
can be used, provided experiments document the validity of values larger than 0 for the type of laminate used.
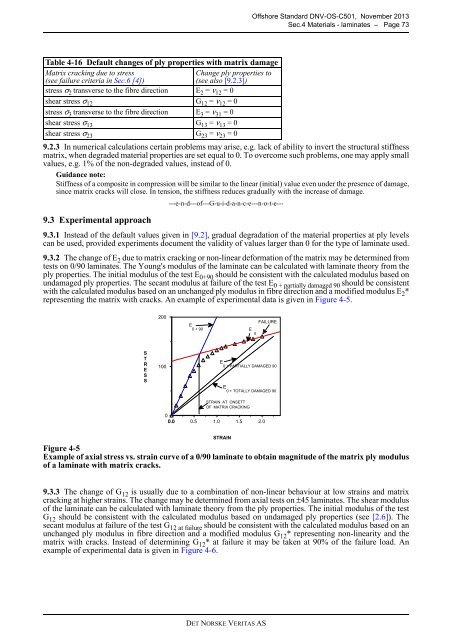
9.3.2 The change of E 2 due to matrix cracking or non-linear deformation of the matrix may be determined from
tests on 0/90 laminates. The Young's modulus of the laminate can be calculated with laminate theory from the
ply properties. The initial modulus of the test E 0+90 should be consistent with the calculated modulus based on
undamaged ply properties. The secant modulus at failure of the test E 0 + partially damaged 90 should be consistent
with the calculated modulus based on an unchanged ply modulus in fibre direction and a modified modulus E 2 *
representing the matrix with cracks. An example of experimental data is given in Figure 4-5.
.
200
E
II
FAILURE
E
0 + 90
E 0 + PARTIALLY DAMAGED 90
S
T
R
E
S
S
100
E 0 + TOTALLY DAMAGED 90
STRAIN AT ONSETT
OF MATRIX CRACKING
0
0.0
0.5
1.0
1.5
2.0
STRAIN
Figure 4-5
Example of axial stress vs. strain curve of a 0/90 laminate to obtain magnitude of the matrix ply modulus
of a laminate with matrix cracks.
9.3.3 The change of G 12 is usually due to a combination of non-linear behaviour at low strains and matrix
cracking at higher strains. The change may be determined from axial tests on ±45 laminates. The shear modulus
of the laminate can be calculated with laminate theory from the ply properties. The initial modulus of the test
G 12 should be consistent with the calculated modulus based on undamaged ply properties (see [2.6]). The
secant modulus at failure of the test G 12 at failure should be consistent with the calculated modulus based on an
unchanged ply modulus in fibre direction and a modified modulus G 12 * representing non-linearity and the
matrix with cracks. Instead of determining G 12 * at failure it may be taken at 90% of the failure load. An
example of experimental data is given in Figure 4-6.
DET NORSKE VERITAS AS