- Page 2 and 3:
Direct Energy Conversion by Andrea
- Page 4 and 5:
CONTENTS i Contents Contents i 1 In
- Page 6 and 7:
CONTENTS iii 6.3.2 Energy Levels in
- Page 8 and 9:
CONTENTS v 9.6 Fuel Cells . . . . .
- Page 10:
Acknowledgements I would like to th
- Page 13 and 14:
2 1.2 Preview of Topics to connect
- Page 15 and 16:
4 1.2 Preview of Topics Math throug
- Page 17 and 18:
6 1.2 Preview of Topics Process Spo
- Page 19 and 20:
8 1.2 Preview of Topics drodynamic
- Page 21 and 22:
10 1.4 Measures of Power and Energy
- Page 23 and 24:
12 1.5 Properties of Materials 1.5
- Page 25 and 26:
14 1.5 Properties of Materials most
- Page 27 and 28:
16 1.6 Electromagnetic Waves −→
- Page 29 and 30:
18 1.6 Electromagnetic Waves Relate
- Page 31 and 32:
20 1.6 Electromagnetic Waves A unif
- Page 33 and 34:
22 1.7 Problems
- Page 35 and 36:
24 2.2 Capacitors 2.2 Capacitors 2.
- Page 37 and 38:
26 2.2 Capacitors 2.2.3 Permittivit
- Page 39 and 40:
28 2.2 Capacitors â z â y â x No
- Page 41 and 42:
30 2.2 Capacitors Figure 2.3: Natur
- Page 43 and 44:
32 2.3 Piezoelectric Devices Piezoe
- Page 45 and 46:
34 2.3 Piezoelectric Devices Lattic
- Page 47 and 48:
36 2.3 Piezoelectric Devices Herman
- Page 49 and 50:
38 2.3 Piezoelectric Devices Figure
- Page 51 and 52:
40 2.3 Piezoelectric Devices c a β
- Page 53 and 54:
42 2.3 Piezoelectric Devices In cer
- Page 55 and 56:
44 2.3 Piezoelectric Devices made m
- Page 57 and 58:
46 2.3 Piezoelectric Devices tions.
- Page 59 and 60:
48 2.4 Problems 2.5. A piezoelectri
- Page 61 and 62:
50 2.4 Problems 2.13. Consider a pi
- Page 63 and 64:
52 2.4 Problems 2.16. The gure belo
- Page 65 and 66:
54 3.2 Pyroelectricity Material Che
- Page 67 and 68:
56 3.3 Electro-Optics KH 2 PO 4 [25
- Page 69 and 70:
58 3.3 Electro-Optics The rst two t
- Page 71 and 72:
60 3.3 Electro-Optics used as an el
- Page 73 and 74:
62 3.4 Notation Quagmire Notation i
- Page 75 and 76: 64 3.5 Problems 3.5 Problems 3.1. F
- Page 77 and 78: 66 3.5 Problems −→ DinC/m 2 unp
- Page 79 and 80: 68 4.1 Introduction Center-fed half
- Page 81 and 82: 70 4.2 Electromagnetic Radiation In
- Page 83 and 84: 72 4.2 Electromagnetic Radiation ar
- Page 85 and 86: 74 4.3 Antenna Components and Denit
- Page 87 and 88: 76 4.4 Antenna Characteristics ante
- Page 89 and 90: 78 4.4 Antenna Characteristics Impe
- Page 91 and 92: 80 4.4 Antenna Characteristics Azim
- Page 93 and 94: 82 4.4 Antenna Characteristics 4.4.
- Page 95 and 96: 84 4.4 Antenna Characteristics 5 Li
- Page 97 and 98: 86 4.5 Problems Figure 4.6: A snow
- Page 99 and 100: 88 4.5 Problems 4.5. Match the foll
- Page 101 and 102: 90 4.5 Problems 4.8. Radiation patt
- Page 103 and 104: 92 5.2 Physics of the Hall Eect The
- Page 105 and 106: 94 5.2 Physics of the Hall Eect The
- Page 107 and 108: 96 5.3 Magnetohydrodynamics This am
- Page 109 and 110: 98 5.5 Applications of Hall Eect De
- Page 111 and 112: 100 5.6 Problems 5.6 Problems 5.1.
- Page 113 and 114: 102 6.2 The Wave and Particle Natur
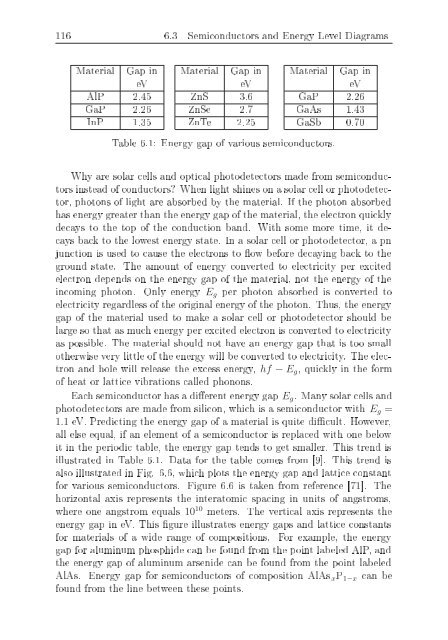
- Page 115 and 116: 104 6.3 Semiconductors and Energy L
- Page 117 and 118: 106 6.3 Semiconductors and Energy L
- Page 119 and 120: 108 6.3 Semiconductors and Energy L
- Page 121 and 122: 110 6.3 Semiconductors and Energy L
- Page 123 and 124: 112 6.3 Semiconductors and Energy L
- Page 125: 114 6.3 Semiconductors and Energy L
- Page 129 and 130: 118 6.3 Semiconductors and Energy L
- Page 131 and 132: 120 6.4 Crystallography Revisited L
- Page 133 and 134: 122 6.5 Pn Junctions E Indirect Sem
- Page 135 and 136: 124 6.5 Pn Junctions an excess of n
- Page 137 and 138: 126 6.5 Pn Junctions V x - + Energy
- Page 139 and 140: 128 6.6 Solar Cells to day and loca
- Page 141 and 142: 130 6.6 Solar Cells dot based mater
- Page 143 and 144: 132 6.7 Photodetectors Solar Panel
- Page 145: 134 6.7 Photodetectors 6.7.2 Measur
- Page 148 and 149: 6 PHOTOVOLTAICS 137 6.3. The gure i
- Page 150 and 151: 7 LAMPS, LEDS, AND LASERS 139 7 Lam
- Page 152 and 153: 7 LAMPS, LEDS, AND LASERS 141 Photo
- Page 154 and 155: 7 LAMPS, LEDS, AND LASERS 143 Absor
- Page 156 and 157: 7 LAMPS, LEDS, AND LASERS 145 We ca
- Page 158 and 159: 7 LAMPS, LEDS, AND LASERS 147 If we
- Page 160 and 161: 7 LAMPS, LEDS, AND LASERS 149 tube
- Page 162 and 163: 7 LAMPS, LEDS, AND LASERS 151 easil
- Page 164 and 165: 7 LAMPS, LEDS, AND LASERS 153 Power
- Page 166 and 167: 7 LAMPS, LEDS, AND LASERS 155 Two L
- Page 168 and 169: 7 LAMPS, LEDS, AND LASERS 157 but n
- Page 170 and 171: 7 LAMPS, LEDS, AND LASERS 159 of ec
- Page 172 and 173: 7 LAMPS, LEDS, AND LASERS 161 the o
- Page 174 and 175: 7 LAMPS, LEDS, AND LASERS 163 Ti:Sa
- Page 176 and 177:
7 LAMPS, LEDS, AND LASERS 165 the b
- Page 178 and 179:
7 LAMPS, LEDS, AND LASERS 167 Gas D
- Page 180 and 181:
7 LAMPS, LEDS, AND LASERS 169 categ
- Page 182 and 183:
7 LAMPS, LEDS, AND LASERS 171 7.8.
- Page 184 and 185:
8 THERMOELECTRICS 173 8 Thermoelect
- Page 186 and 187:
8 THERMOELECTRICS 175 Symbol Name V
- Page 188 and 189:
8 THERMOELECTRICS 177 per unit volu
- Page 190 and 191:
8 THERMOELECTRICS 179 kPa, and the
- Page 192 and 193:
8 THERMOELECTRICS 181 Seebeck Effec
- Page 194 and 195:
8 THERMOELECTRICS 183 gradient acro
- Page 196 and 197:
8 THERMOELECTRICS 185 thermocouples
- Page 198 and 199:
8 THERMOELECTRICS 187 The gure of m
- Page 200 and 201:
8 THERMOELECTRICS 189 or mass invol
- Page 202 and 203:
8 THERMOELECTRICS 191 temperatures?
- Page 204 and 205:
8 THERMOELECTRICS 193 Figure 8.4: L
- Page 206 and 207:
8 THERMOELECTRICS 195 8.9 Problems
- Page 208 and 209:
8 THERMOELECTRICS 197 8.8. A thermo
- Page 210:
8 THERMOELECTRICS 199 Figure 8.5 8.
- Page 213 and 214:
202 9.2 Measures of the Ability of
- Page 215 and 216:
204 9.2 Measures of the Ability of
- Page 217 and 218:
206 9.2 Measures of the Ability of
- Page 219 and 220:
208 9.2 Measures of the Ability of
- Page 221 and 222:
210 9.2 Measures of the Ability of
- Page 223 and 224:
212 9.3 Charge Flow in Batteries an
- Page 225 and 226:
214 9.3 Charge Flow in Batteries an
- Page 227 and 228:
216 9.4 Measures of Batteries and F
- Page 229 and 230:
218 9.4 Measures of Batteries and F
- Page 231 and 232:
220 9.4 Measures of Batteries and F
- Page 233 and 234:
222 9.4 Measures of Batteries and F
- Page 235 and 236:
224 9.5 Battery Types specic energi
- Page 237 and 238:
226 9.5 Battery Types at the anode
- Page 239 and 240:
228 9.5 Battery Types Figure 9.8: T
- Page 241 and 242:
230 9.6 Fuel Cells Fuel cell compon
- Page 243 and 244:
232 9.6 Fuel Cells 9.6.3 Practical
- Page 245 and 246:
234 9.7 Problems 9.7 Problems 9.1.
- Page 247 and 248:
236 9.7 Problems A E - + I B D H 2
- Page 249 and 250:
238 10.3 Radiation Detectors high e
- Page 251 and 252:
240 10.5 Resistive Sensors capacito
- Page 253 and 254:
242 10.6 Electrouidics However, ene
- Page 255 and 256:
244 10.6 Electrouidics
- Page 257 and 258:
246 11.2 Lagrangian and Hamiltonian
- Page 259 and 260:
248 11.3 Principle of Least Action
- Page 261 and 262:
250 11.4 Derivation of the Euler-La
- Page 263 and 264:
252 11.5 Mass Spring Example not in
- Page 265 and 266:
254 11.5 Mass Spring Example Path 1
- Page 267 and 268:
256 11.5 Mass Spring Example We can
- Page 269 and 270:
258 11.6 Capacitor Inductor Example
- Page 271 and 272:
260 11.6 Capacitor Inductor Example
- Page 273 and 274:
262 11.7 Schrödinger's Equation 11
- Page 275 and 276:
264 11.8 Problems 11.4. Figure 11.2
- Page 277 and 278:
266 11.8 Problems a famous result k
- Page 279 and 280:
268 11.8 Problems (c) Find the gene
- Page 281 and 282:
270 12.2 Electrical Energy Conversi
- Page 283 and 284:
272 12.2 Electrical Energy Conversi
- Page 285 and 286:
274 12.2 Electrical Energy Conversi
- Page 287 and 288:
276 12.3 Mechanical Energy Conversi
- Page 289 and 290:
278 12.3 Mechanical Energy Conversi
- Page 291 and 292:
280 12.3 Mechanical Energy Conversi
- Page 293 and 294:
282 12.4 Thermodynamic Energy Conve
- Page 295 and 296:
284 12.4 Thermodynamic Energy Conve
- Page 297 and 298:
286 12.5 Chemical Energy Conversion
- Page 299 and 300:
288 12.6 Problems 12.6 Problems 12.
- Page 301 and 302:
290 12.6 Problems 12.6. Match the d
- Page 303 and 304:
292 13.1 Introduction • Describe
- Page 305 and 306:
294 13.2 Preliminary Ideas Assuming
- Page 307 and 308:
296 13.3 Derivation of the Lagrangi
- Page 309 and 310:
298 13.3 Derivation of the Lagrangi
- Page 311 and 312:
300 13.3 Derivation of the Lagrangi
- Page 313 and 314:
302 13.3 Derivation of the Lagrangi
- Page 315 and 316:
304 13.3 Derivation of the Lagrangi
- Page 317 and 318:
306 13.4 Deriving the Thomas Fermi
- Page 319 and 320:
308 13.5 From Thomas Fermi Theory t
- Page 321 and 322:
310 13.6 Problems (a) Write the Ham
- Page 323 and 324:
312 14.1 Introduction damental equa
- Page 325 and 326:
314 14.2 Types of Symmetries be wri
- Page 327 and 328:
316 14.3 Continuous Symmetries and
- Page 329 and 330:
318 14.3 Continuous Symmetries and
- Page 331 and 332:
320 14.3 Continuous Symmetries and
- Page 333 and 334:
322 14.4 Derivation of the Innitesi
- Page 335 and 336:
324 14.4 Derivation of the Innitesi
- Page 337 and 338:
326 14.4 Derivation of the Innitesi
- Page 339 and 340:
328 14.4 Derivation of the Innitesi
- Page 341 and 342:
330 14.5 Invariants and we end up w
- Page 343 and 344:
332 14.5 Invariants in the limit ε
- Page 345 and 346:
334 14.5 Invariants Next use Eq. 14
- Page 347 and 348:
336 14.6 Summary 14.6 Summary In th
- Page 349 and 350:
338 14.7 Problems 14.6. The equatio
- Page 351 and 352:
340 14.7 Problems
- Page 353 and 354:
342 Appendices Symbol Quantity Unit
- Page 355 and 356:
344 Appendices Symbol Quantity Unit
- Page 357 and 358:
346 Appendices Symbol Quantity Unit
- Page 359 and 360:
348 Appendices Symbol Quantity Unit
- Page 361 and 362:
350 Appendices Prex name Symbol Val
- Page 363 and 364:
352 Appendices for voltage. (As an
- Page 365 and 366:
354 Appendices Material or Device S
- Page 367 and 368:
356 REFERENCES [15] E. C. Jordan an
- Page 369 and 370:
358 REFERENCES [45] V. K. Tikhomiro
- Page 371 and 372:
360 REFERENCES [73] M. G. Thomas, H
- Page 373 and 374:
362 REFERENCES [100] A. Ishibashi,
- Page 375 and 376:
364 REFERENCES [125] D. Wright, Req
- Page 377 and 378:
366 REFERENCES [150] J. P. Owejan,
- Page 379 and 380:
368 REFERENCES [175] G. K. Woodgate
- Page 381 and 382:
Index Absorption, 139 Action, 247 A
- Page 383 and 384:
372 INDEX Nernst equation, 220 Neur
- Page 385:
About the Book Direct Energy Conver