SpÄļu teorijas mÄcÄ«bu materiÄli (.pdf) - Fizmati
SpÄļu teorijas mÄcÄ«bu materiÄli (.pdf) - Fizmati
SpÄļu teorijas mÄcÄ«bu materiÄli (.pdf) - Fizmati
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
u(y)<br />
✻<br />
2<br />
<br />
<br />
1<br />
<br />
<br />
✲<br />
0 1 4 y<br />
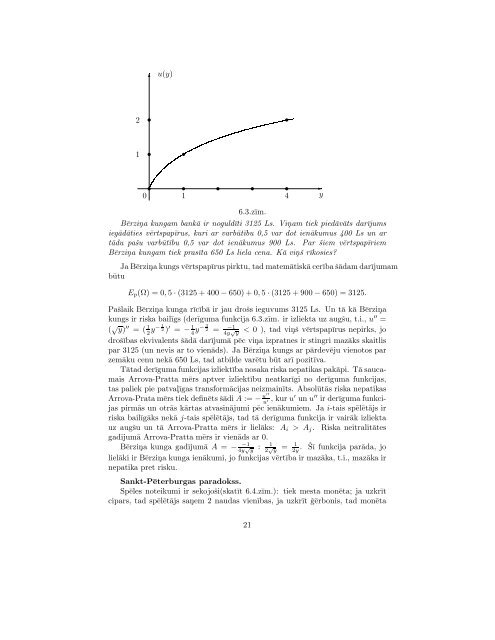
6.3.zīm.<br />
Bērziņa kungam bankā irnoguldīti 3125 Ls. Viņam tiek piedāvāts darījums<br />
iegādāties vērtspapīrus, kuri ar varbūtību 0,5 var dot ienākumus 400 Ls un ar<br />
tādu pašu varbūtību 0,5 var dot ienākumus 900 Ls. Par šiem vērtspapīriem<br />
Bērziņa kungam tiek prasīta 650 Ls liela cena. Kā viņš rīkosies<br />
Ja Bērziņa kungs vērtspapīrus pirktu, tad matemātiskā cerība šādam darījumam<br />
būtu<br />
E p (Ω) = 0, 5 · (3125 + 400 − 650) + 0, 5 · (3125 + 900 − 650) = 3125.<br />
Pašlaik Bērziņa kunga rīcībā irjaudrošs ieguvums 3125 Ls. Un tā kāBērziņa<br />
kungs ir riska bailīgs (derīguma funkcija 6.3.zīm. ir izliekta uz augšu, t.i., u ′′ =<br />
( √ y) ′′ =( 1 2 y− 1 2 ) ′ = − 1 4 y− 3 2 = −1<br />
4y √ y<br />
< 0),tadviņš vērtspapīrus nepirks, jo<br />
drošības ekvivalents šādā darījumā pēc viņa izpratnes ir stingri mazāks skaitlis<br />
par 3125 (un nevis ar to vienāds). Ja Bērziņa kungs ar pārdevēju vienotos par<br />
zemāku cenu nekā 650 Ls, tad atbilde varētu būt arī pozitīva.<br />
Tātad derīguma funkcijas izliektība nosaka riska nepatikas pakāpi. Tāsaucamais<br />
Arrova-Pratta mērs aptver izliektību neatkarīgi no derīguma funkcijas,<br />
tas paliek pie patvaļīgas transformācijas neizmainīts. Absolūtās riska nepatikas<br />
Arrova-Prata mērs tiek definēts šādi A := − u′′<br />
u<br />
,kuru ′ un u ′′ ir derīguma funkcijas<br />
pirmās un otrās kārtas atvasinājumi pēc ienākumiem. Ja i-tais spēlētājs ir<br />
′<br />
riska bailīgāks nekā j-tais spēlētājs, tad tā derīguma funkcija ir vairāk izliekta<br />
uz augšu un tā Arrova-Pratta mērs ir lielāks: A i >A j . Riska neitralitātes<br />
gadījumā Arrova-Pratta mērs ir vienāds ar 0.<br />
Bērziņa kunga gadījumā A = − −1<br />
4y √ y : 1<br />
2 √ y = 1<br />
2y .<br />
Šī funkcija parāda, jo<br />
lielāki ir Bērziņa kunga ienākumi, jo funkcijas vērtība ir mazāka, t.i., mazāka ir<br />
nepatika pret risku.<br />
Sankt-Pēterburgas paradokss.<br />
Spēles noteikumi ir sekojoši(skatīt 6.4.zīm.): tiek mesta monēta; ja uzkrīt<br />
cipars, tad spēlētājs saņem 2 naudas vienības, ja uzkrīt ǧērbonis, tad monēta<br />
21