1. Introduction - Firenze University Press

More documents

Recommendations

Info

Electricity distribution (EE) D Ep Es P S P Natural gas GT + Heat recovery Gas engine + Heat recovery Steam, 180°C 331 Steam boiler Steam/Hot Water HX Hot Water Boiler Hot Water, 90°C Hot Water/ Cooling Water HX Cooling water, ambient + 5°C 2x effect 1x effect EE EE EE Abs Abs Mechanical EE Chiller Chiller Chiller Chilled water, 5°C Cooling tower Figure 2 Superstructure of energy supply system for a hospital. D Heating Ambient Air D W Coolth 4. Optimal Mine Site Energy Supply – OMSES initial formulation For energy services superstructures such as those presented in Figures 1 and 2, following precedent practices [32] [34]], the decision variables for an optimization problem formulated to determine the optimal mine site energy supply may be characterized as follows: i) binary variables (denoting whether a technology is/is not installed); ii) integer variables (denoting the number of installed units of a technology); iii) continuous variables (denoting the energy flows between utilities). The latter include connections to distribution systems across the site boundary (to the utility company’s electrical and natural gas distribution systems – where appropriate) and energy flows between distributions and site loads. The constraints that may be taken to apply to the optimization process are manifold: <strong>1.</strong> Energy conversion technology constraints. These are constraints that reflect an energy conversion mass and energy balance across each technology of a specific type. A graphical example representation of such a constraint is presented in Figure 3 which shows the energy (and inferred mass) balance across a gas turbine equipped with a heat recovery unit. 2. Technology installation limit constraints. These constraints apply a threshold on the maximum number of units of a given technology type that may be installed. Such a constraint is useful to reflect practical considerations such as the amount of land footprint available to accommodate technology of a specific type. This also articulates a capacity constraint for the specific technologies. 3. Utility balancing off constraints. These are constraints that ensure that the net sums of energy flows from each of the indicated distributions are zero, which also ensure that energy supply (in all its forms) meets on-site demand. In the event that hourly on-site demand data
are available for an entire year, 8760 such constraints feature in the problem formulation, for a specific utility. In practice, various heuristics may be deployed to reduce the number of these constraints (e.g., considering only 12, 24 hour periods, each representative of a typical day in a typical month – see Figure 4). 4. Carbon dioxide equivalent emissions constraints. These are constraints that express the idea that the total emissions associated with the production of energy from the energy services system falls below a given threshold. In prior formulations [e.g., [32] [33]], such emissions include those attributable to the materials (manufacture and installation of the technologies at the site) and operation of the system. 5. Energy market constraints. These include inter alia thresholds on the quantities of energy that may be procured externally, exported off-site, or wasted. Figure 3: Showing (LHS) a cut-away diagram of a Capstone C600 gas turbine [35] and (RHS) the energy flows for this technology normalized to the electrical energy output. The objective function for the optimization process is defined in economic terms, expressed as a minimum total cost of meeting the on-site energy demand. Various components are considered in its formulation. Principally, the total cost is decomposed into an annuitized fixed cost element and a variable cost element. The fixed cost element thus accounts for the discounting process and the time value of money, as well as the replacement / major overhaul interval of the technology. The variable cost element is primarily expressed in terms of the unit cost of procurement of energy in a particular form, supplied to the site, multiplied by the volume of that energy used in a specified time period. Through constraints taken to apply in the optimization process, this cost element may reflect particular operational strategies imposed, for example, a user-defined decision to operate bespoke cogeneration plant components at full load. As it is within the scope of the energy services infrastructure to export energy in various forms off the site, revenues arising from any such sales are treated as negative costs. Given the nature of the decision variables indicated, in prior deployments Mixed Integer Programming (MIP) has been found effective in establishing optimal configurations and equipment operating strategies, this technique having been broadly applied in production planning, sequencing processes, distribution and logistics problems, refinery planning, power plant scheduling, and process design. MIP captures the complexity of polygeneration systems in synthesis problems such as that described for optimal on-site energy supply. Formulation of the problem in MIP compatible terms presents opportunities to benefit from significant recent advances in the mathematical programming field such as those found in [36]. 332
Page 1:
Proceedings e report 90
Page 4 and 5:
ECOS 2012 : the 25 th International
Page 7 and 8:
Advisory Committee (Track Organizer
Page 10 and 11:
The 25 th ECOS Conference 1987-2012
Page 12 and 13:
VOLUME VI CONTENT VI. 1 CARBON CAPT
Page 14 and 15:
-----------------------------------
Page 16 and 17:
» Personal transportation energy c
Page 18 and 19:
» Excess enthalpies of second gene
Page 20 and 21:
VOLUME IV IV . 1 - FLUID DYNAMICS A
Page 22 and 23:
» Exergy analysis and genetic algo
Page 24 and 25:
» Optimal lighting control strateg
Page 26 and 27:
» Stability and limit cycles in an
Page 28 and 29:
PROCEEDINGS OF ECOS 2012 - THE 25 T
Page 30 and 31:
Fig. 2. The exergy destruction of M
Page 32 and 33:
ineffectiveness of the catalyst, in
Page 34 and 35:
[ P EXmth EX SNG] ESR F where EXm
Page 36 and 37:
Fuel inputkW 728221 203771 237719 3
Page 38 and 39:
Not only at desined Rc (the ratio o
Page 40 and 41:
4. DISCUSSION The graphic exergy an
Page 42 and 43:
Figure 9(a) illustrates the energy
Page 44 and 45:
Engineering Technical Conferences &
Page 46 and 47:
generally there are four kinds of m
Page 48 and 49:
However, even under the off-design
Page 50 and 51:
Fig. 3. 600MW supercritical coal-fi
Page 52 and 53:
CO2 rich loading(molCO2/molMEA) 0.4
Page 54 and 55:
Net efficiency (%) 40.28 30.29 26.4
Page 56 and 57:
Fig. 11. Schematic diagram of heat
Page 58 and 59:
28.67%. In addition, through heat i
Page 60 and 61:
Applied Thermal Engineering 2010;30
Page 62 and 63:
Abstract: PROCEEDINGS OF ECOS 2012
Page 64 and 65:
Fig. 1. Solution diagram of „four
Page 66 and 67:
K ~ K 1 eK 1a p K 1a iK mK
Page 68 and 69:
Oxygen recovery rate, % 105 95 85 7
Page 70 and 71:
Calculated optimal compressor press
Page 72 and 73:
Page 74 and 75:
The net amount of the flue gas leav
Page 76 and 77:
Figure 3. Idea for lignite drying b
Page 78 and 79:
Energy efficiency, % 34,00 33,00 32
Page 80 and 81:
points efficiency increase related
Page 82 and 83:
Figure A1b. Thermoflex flow sheet o
Page 84 and 85:
Figure A3a. Thermoflex flow sheet o
Page 86 and 87:
Figure A4. Thermoflex flow sheet of
Page 88 and 89:
Page 90 and 91:
2.1. Life Cycle Assessment 2.1.1. G
Page 92 and 93:
these factors. A sensitivity analys
Page 94 and 95:
methane slip contributes to 13% of
Page 96 and 97:
As can be seen in Fig. 5 the impact
Page 98 and 99:
References [1] Eurobserv’er, The
Page 100 and 101:
Page 102 and 103:
in which CO2 is separated from H2,
Page 104 and 105:
dimensions of water droplets and wa
Page 106 and 107:
Temperature (°C) 8 7 6 5 4 3 2 1 0
Page 108 and 109:
4. Conclusions In the present paper
Page 110 and 111:
Page 112 and 113:
penalty, but without separate captu
Page 114 and 115:
0.5 - 0.7 kg/kg, resulting typicall
Page 116 and 117:
3.3 - Utilising waste heat All exis
Page 118 and 119:
4.5 - Suomusjärvi olivine deposits
Page 120 and 121:
material will change from a few % t
Page 122 and 123:
Fig. 5 Schematic diagram of the PFB
Page 124 and 125:
8. Combined SO2 capture and CO2 min
Page 126 and 127:
Fig. 10 Carbonate- (left) and sulph
Page 128 and 129:
[13] Ekdahl, E., Idman, H. Statemen
Page 130 and 131:
Page 132 and 133:
HEAT Fig. 1. Scheme and main reacti
Page 134:
(raw) materials pre-heating and AS
Page 137 and 138:
Fig 3- Aspen Plus® model 110
Page 139 and 140:
Table 4. Elemental and XRD analysis
Page 141 and 142:
the ÅA CSM route. The content of M
Page 143 and 144:
Page 145 and 146:
moisture - 0,2237 ash - 0,0876 LHV
Page 147 and 148:
2.2 CFB plant For the current momen
Page 149 and 150:
The CO2 emission factor which indic
Page 151 and 152:
The CO2 emission factor calculated
Page 153 and 154:
Appendix A Fig A.1. Simulation mode
Page 155 and 156:
(b) Fig. A.2. Simulation model of C
Page 157 and 158:
Table A.1. Calculated parameters at
Page 159 and 160:
References [1] Pfaff I., Oexmann J.
Page 161 and 162:
with a CC installation could be avo
Page 163 and 164:
2.3. Basic CHP plant indices. The b
Page 165 and 166:
3. Off-design calculations The main
Page 167 and 168:
Fig. 6. CHP plant efficiency Fig. 7
Page 169 and 170:
amount of steam delivered to the he
Page 171 and 172:
[5] Lukowicz H., Mroncz M.: Analysi
Page 173 and 174:
water removal is feasible by coolin
Page 175 and 176:
Figure 2. Sketch of the suggested P
Page 177 and 178:
a b Figure 5. a) Exergy balance of
Page 179 and 180:
The basis of comparison of each met
Page 181 and 182:
Figure 7a. Impact of S/CATR on PCU
Page 183 and 184:
However, more energy duty is requir
Page 185 and 186:
Page 187 and 188:
3.1. JACOBIAN-ASPEN Interface ASPEN
Page 189 and 190:
Fig. 3. Triple Pressure Bottoming S
Page 191 and 192:
As seen from Table 1, the mass flow
Page 193 and 194:
4. Conclusion Fig. 5. Partial Emiss
Page 195 and 196:
[19] Yantovski E., Shokotov M., Sho
Page 197 and 198:
investigation and the developing of
Page 199 and 200:
University of L’Aquila and German
Page 201 and 202:
hydrogen combustion technology at d
Page 203 and 204:
eversibility of a pre-treated synth
Page 205 and 206:
Fig. 1. TG curves collected for spe
Page 207 and 208:
(see Fig 5). Carbon dioxide uptake
Page 209 and 210:
period is reduced to the first 15 c
Page 211 and 212:
CO2 capture capacity up to 150 th c
Page 213 and 214:
the way for biogas utilisation is t
Page 215 and 216:
projectand is described in the foll
Page 217 and 218:
4. Pilot plant tests In order to de
Page 219 and 220:
Concerning the absorption reaction,
Page 221 and 222:
with Regeneration (AwR), consists i
Page 223 and 224:
[25] Aspen Plus 2004.1. Cambridge,
Page 225 and 226:
systems for fuel drying waste strea
Page 227 and 228:
heated in a heat exchanger placed i
Page 229 and 230:
Fig. 2. Lower heating value of fuel
Page 231 and 232:
Acknowledgements The results presen
Page 233 and 234:
large amount of CO2 [1,5-7]. APCr a
Page 235 and 236:
N 1 i ( x x i n 1 m ) 2.3. Carbon
Page 237 and 238:
DTA analysis of the untreated APCrs
Page 239 and 240:
Table 4. Relative Error (%) of the
Page 241 and 242:
CaO HCl CaCl H O 193kJ / mol (
Page 243 and 244:
[1] M. Fernández Bertos, S.J.R. Si
Page 245 and 246:
Page 247 and 248:
2. Process development 2.1. Backgro
Page 249 and 250:
to dissolve the chloride salts prec
Page 251 and 252:
The remaining 25% (5 ml/min) of the
Page 253 and 254:
Table 6. Experimental conversions o
Page 255 and 256:
p p 1 1. 5 p H 1 1. 5 2O p mi
Page 257 and 258:
Calculating from the Aspen Plus mod
Page 259 and 260:
[11] Mattila, H.-P., Experimental s
Page 261 and 262:
Mg2SiO4(s) + 2CO2(g) →2MgCO3(s) +
Page 263 and 264:
(Mg/Fe) of the mineral rock, Mg-sil
Page 265 and 266:
Figure 2. Effect of Mg/Fe ratio of
Page 267 and 268:
Figure 4 shows that an increase in
Page 269 and 270:
Figure 5. Process flow diagram of M
Page 271 and 272:
2. Only cold utility is needed belo
Page 273 and 274:
extraction process at 400 °C (~ 62
Page 275 and 276:
Table A2. Extraction equations and
Page 277 and 278:
[13] Teir S, Kuusik R, Fogelholm CJ
Page 279 and 280:
In the area of coal technologies al
Page 281 and 282:
Tabel 1. Characteristics quantities
Page 283 and 284:
N m eT 4a ~ T cp T4a 1 ( K
Page 285 and 286:
Auxiliary power rate of ASU, % 40 4
Page 287 and 288:
[8] Buhre B.J.P., Elliott L.K., She
Page 289 and 290:
1.1 - Cement Manufacturing The ceme
Page 291 and 292:
2. Numerical model The purpose of t
Page 293 and 294:
-0.309x15.77x2 2.085x3 240x4 12.53x
Page 295 and 296:
Table 4 - Results of the optimizati
Page 297 and 298:
Page 299 and 300:
1. Define the studied system (in th
Page 301 and 302:
cycle) or a lignin extraction plant
Page 303 and 304:
limiting factor for the maximum siz
Page 305 and 306:
Table 5. Key data for the four ener
Page 307 and 308: Global CO 2 emissions [ktonnes/yr]
Page 309 and 310: for biofuels and the investment cos
Page 311 and 312: The possibility to capture CO2 from
Page 313 and 314: [17] Berglin N, Andersson L. Proces
Page 315 and 316: Therefore NL Agency (an agency of t
Page 317 and 318: 2.2.2. Pinch analysis Pinch analysi
Page 319 and 320: 3. Case study 3.1. Plant and proces
Page 321 and 322: Te 1000 mp era 900 tur 800 e [°C 7
Page 323 and 324: Application of the approach led to
Page 325 and 326: The advantage of dynamic models is
Page 327 and 328: e equal at both time intervals and
Page 329 and 330: 2.5. Selecting the number of TSs Se
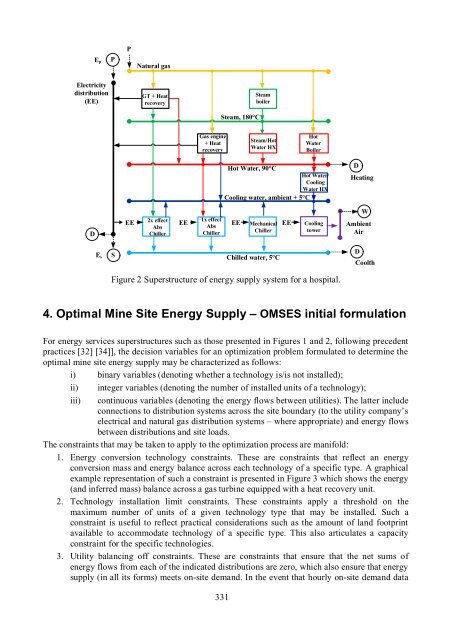
Page 331 and 332: A) Time Slices for solar thermal en
Page 333 and 334: The first step of procedure is to p
Page 335 and 336: cTSs demand TS solar TSs 0 2 4 6 8
Page 337 and 338: In the presented paper a framework
Page 339 and 340: [5] Erdil E, Ilkan M, Egelioglu F.
Page 341 and 342: PROCEEDINGS OF ECOS 2012 - THE 25 T
Page 343 and 344: district energy network simulation
Page 345 and 346: were decreased by 10°C.All scenari
Page 347 and 348: Site 3 Heat sources Heat load Site
Page 349 and 350: 3.2.2. Input data and assumptions A
Page 351 and 352: Fig.7 shows the operation forecast
Page 353 and 354: [13] TERMIS Operation User Guide, 7
Page 355 and 356: Polygeneration is a term used to de
Page 357: The increase in energy utilization
Page 361 and 362: 6. Extensions to core methodology 6
Page 363 and 364: thermal storage and possible suppor
Page 365 and 366: laterites. Ore Geology Reviews, v.
Page 367 and 368: Abstract: PROCEEDINGS OF ECOS 2012
Page 369 and 370: gasification [15], hybrid biomass g
Page 371 and 372: the second reactor. In this unit, s
Page 373 and 374: The variables effect was evaluated
Page 375 and 376: atio, as well as the shift-syngas f
Page 377 and 378: Fig. 4. Effect of operating tempera
Page 379 and 380: SDG has slight effect on the syngas
Page 381: [26.] Castle WF. Air separation and
show all

1. Introduction - Firenze University Press

Create successful ePaper yourself

Delete template?

Save as template?