- Page 1 and 2: Data Bank ISBN 92-64-02145-0 PENELO
- Page 3 and 4: FOREWORD The OECD/NEA Data Bank was
- Page 5 and 6: TABLE OF CONTENTS Foreword ........
- Page 7 and 8: 4.3 Combined scattering and energy
- Page 9 and 10: PREFACE Radiation transport in matt
- Page 11 and 12: The present version of PENELOPE is
- Page 13 and 14: Chapter 1 Monte Carlo simulation. B
- Page 15 and 16: 1.1. Elements of probability theory
- Page 17 and 18: 1.1. Elements of probability theory
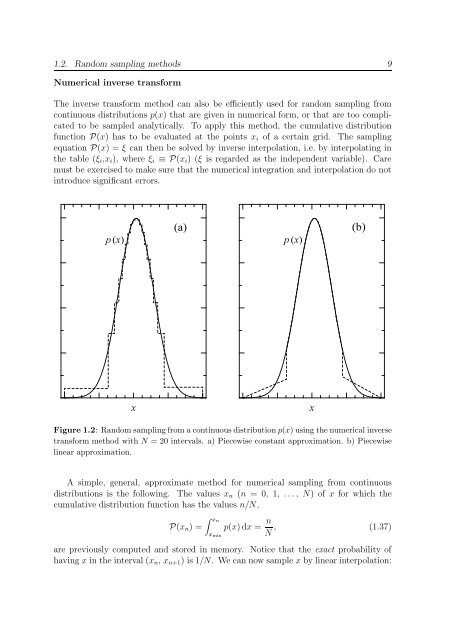
- Page 19: 1.2. Random sampling methods 7 Tabl
- Page 23 and 24: 1.2. Random sampling methods 11 whe
- Page 25 and 26: 1.2. Random sampling methods 13 can
- Page 27 and 28: 1.2. Random sampling methods 15 mus
- Page 29 and 30: 1.2. Random sampling methods 17 the
- Page 31 and 32: 1.3. Monte Carlo integration 19 Con
- Page 33 and 34: 1.4. Simulation of radiation transp
- Page 35 and 36: 1.4. Simulation of radiation transp
- Page 37 and 38: ¡ ¢ 1.4. Simulation of radiation
- Page 39 and 40: 1.4. Simulation of radiation transp
- Page 41 and 42: 1.5. Statistical averages and uncer
- Page 43 and 44: 1.6. Variance reduction 31 also imp
- Page 45 and 46: 1.6. Variance reduction 33 weight a
- Page 47 and 48: Chapter 2 Photon interactions In th
- Page 49 and 50: 2.1. Coherent (Rayleigh) scattering
- Page 51 and 52: 2.1. Coherent (Rayleigh) scattering
- Page 53 and 54: 2.2. Photoelectric effect 41 ➤E E
- Page 55 and 56: F 2.2. Photoelectric effect 43 1E+7
- Page 57 and 58: 2.3. Incoherent (Compton) scatterin
- Page 59 and 60: C u 2.3. Incoherent (Compton) scatt
- Page 61 and 62: 2.3. Incoherent (Compton) scatterin
- Page 63 and 64: 2.3. Incoherent (Compton) scatterin
- Page 65 and 66: 2.3. Incoherent (Compton) scatterin
- Page 67 and 68: 2.4. Electron-positron pair product
- Page 69 and 70: 2.4. Electron-positron pair product
- Page 71 and 72:
2.4. Electron-positron pair product
- Page 73 and 74:
2.4. Electron-positron pair product
- Page 75 and 76:
2.5. Attenuation coefficients 63 di
- Page 77 and 78:
2.6. Atomic relaxation 65 2.6 Atomi
- Page 79 and 80:
2.6. Atomic relaxation 67 two vacan
- Page 81 and 82:
Chapter 3 Electron and positron int
- Page 83 and 84:
3.1. Elastic collisions 71 nucleus
- Page 85 and 86:
3.1. Elastic collisions 73 1 E - 1
- Page 87 and 88:
ρ ρ ρ λ λ λ ρ ρ ρ λ λ λ
- Page 89 and 90:
3.1. Elastic collisions 77 becomes
- Page 91 and 92:
B ' B ' 3.1. Elastic collisions 79
- Page 93 and 94:
3.2. Inelastic collisions 81 where
- Page 95 and 96:
3.2. Inelastic collisions 83 global
- Page 97 and 98:
3.2. Inelastic collisions 85 plays
- Page 99 and 100:
3.2. Inelastic collisions 87 optica
- Page 101 and 102:
3.2. Inelastic collisions 89 The DC
- Page 103 and 104:
3.2. Inelastic collisions 91 In the
- Page 105 and 106:
3.2. Inelastic collisions 93 where
- Page 107 and 108:
c b c b 3.2. Inelastic collisions 9
- Page 109 and 110:
A l A u 3.2. Inelastic collisions 9
- Page 111 and 112:
3.2. Inelastic collisions 99 After
- Page 113 and 114:
3.2. Inelastic collisions 101 Table
- Page 115 and 116:
3.2. Inelastic collisions 103 In re
- Page 117 and 118:
3.2. Inelastic collisions 105 1Ε+4
- Page 119 and 120:
3.3. Bremsstrahlung emission 107 an
- Page 121 and 122:
3.3. Bremsstrahlung emission 109 1
- Page 123 and 124:
3.3. Bremsstrahlung emission 111 1
- Page 125 and 126:
3.3. Bremsstrahlung emission 113 wh
- Page 127 and 128:
3.3. Bremsstrahlung emission 115 Al
- Page 129 and 130:
3.3. Bremsstrahlung emission 117 Th
- Page 131 and 132:
3.4. Positron annihilation 119 (198
- Page 133 and 134:
3.4. Positron annihilation 121 It i
- Page 135 and 136:
Chapter 4 Electron/positron transpo
- Page 137 and 138:
4.1. Elastic scattering 125 Lewis (
- Page 139 and 140:
4.1. Elastic scattering 127 ⎡ ⎛
- Page 141 and 142:
4.1. Elastic scattering 129 simulat
- Page 143 and 144:
4.1. Elastic scattering 131 The sim
- Page 145 and 146:
4.2. Soft energy losses 133 soft in
- Page 147 and 148:
4.2. Soft energy losses 135 deviati
- Page 149 and 150:
4.2. Soft energy losses 137 scatter
- Page 151 and 152:
4.3. Combined scattering and energy
- Page 153 and 154:
4.3. Combined scattering and energy
- Page 155 and 156:
4.3. Combined scattering and energy
- Page 157 and 158:
4.3. Combined scattering and energy
- Page 159 and 160:
4.4. Generation of random tracks 14
- Page 161 and 162:
4.4. Generation of random tracks 14
- Page 163 and 164:
4.4. Generation of random tracks 15
- Page 165 and 166:
Chapter 5 Constructive quadric geom
- Page 167 and 168:
5.1. Rotations and translations 155
- Page 169 and 170:
5.2. Quadric surfaces 157 Given a f
- Page 171 and 172:
5.2. Quadric surfaces 159 Table 5.1
- Page 173 and 174:
5.3. Constructive quadric geometry
- Page 175 and 176:
5.4. Geometry definition file 163 1
- Page 177 and 178:
5.4. Geometry definition file 165
- Page 179 and 180:
5.5. The subroutine package pengeom
- Page 181 and 182:
5.5. The subroutine package pengeom
- Page 183 and 184:
5.6. Debugging and viewing the geom
- Page 185 and 186:
5.7. A short tutorial 173 MODULE (
- Page 187 and 188:
5.7. A short tutorial 175 Writing a
- Page 189 and 190:
Chapter 6 Structure and operation o
- Page 191 and 192:
6.1. penelope 179 and/or numbers in
- Page 193 and 194:
6.1. penelope 181 1986). The format
- Page 195 and 196:
6.1. penelope 183 The connection of
- Page 197 and 198:
6.1. penelope 185 that has to be lo
- Page 199 and 200:
G y y y y y 6.1. penelope 187 CALL
- Page 201 and 202:
6.1. penelope 189 It is the respons
- Page 203 and 204:
6.2. Examples of MAIN programs 191
- Page 205 and 206:
6.2. Examples of MAIN programs 193
- Page 207 and 208:
6.2. Examples of MAIN programs 195
- Page 209 and 210:
6.2. Examples of MAIN programs 197
- Page 211 and 212:
6.2. Examples of MAIN programs 199
- Page 213 and 214:
6.3. Selecting the simulation param
- Page 215 and 216:
! 6.3. Selecting the simulation par
- Page 217 and 218:
6.5. Installation 205 radiation is
- Page 219 and 220:
6.5. Installation 207 To get the ex
- Page 221 and 222:
Appendix A Collision kinematics To
- Page 223 and 224:
A.1. Two-body reactions 211 Clearly
- Page 225 and 226:
A.2. Inelastic collisions of charge
- Page 227 and 228:
m A.2. Inelastic collisions of char
- Page 229 and 230:
Appendix B Numerical tools B.1 Cubi
- Page 231 and 232:
B.1. Cubic spline interpolation 219
- Page 233 and 234:
B.2. Numerical quadrature 221 B.2 N
- Page 235 and 236:
Appendix C Electron/positron transp
- Page 237 and 238:
C.1. Tracking particles in vacuum.
- Page 239 and 240:
C.1. Tracking particles in vacuum.
- Page 241 and 242:
C.2. Exact tracking in homogeneous
- Page 243 and 244:
C.2. Exact tracking in homogeneous
- Page 245 and 246:
Bibliography Abramowitz M. and I.A.
- Page 247 and 248:
Bibliography 235 Briesmeister J.F.
- Page 249 and 250:
Bibliography 237 James F. (1990),
- Page 251 and 252:
Bibliography 239 Reimer L. and E.R.
- Page 253:
Bibliography 241 Yates A.C. (1968),