PENELOPE 2003 - OECD Nuclear Energy Agency

78 Chapter 3. Electron and positron interactions
1 E - 1 2
1 E - 1 3
1 E - 1 4
A u ( Z = 7 9 ) , e −
p a r t i a l w a v e
M W m o d el
1 E - 1 5
dσ el
/dµ (cm 2 )
1 E - 1 6
1 E - 1 7
1 E - 1 8
1 E - 1 9
1 keV
10
10 0
1 E - 20
1 E - 21
10 0 0
1 E - 22
1 E - 6 1 E - 5 1 E - 4 1 E - 3 0.01
µ
0.2 0.4 0.6 0.8 1 .0
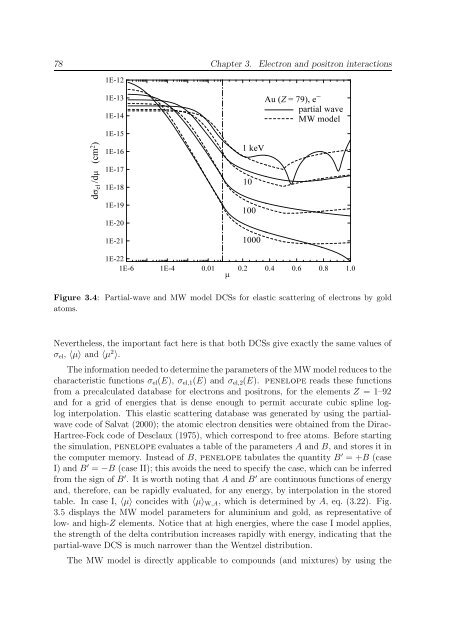
Figure 3.4: Partial-wave and MW model DCSs for elastic scattering of electrons by gold
atoms.
Nevertheless, the important fact here is that both DCSs give exactly the same values of
σ el , 〈µ〉 and 〈µ 2 〉.
The information needed to determine the parameters of the MW model reduces to the
characteristic functions σ el (E), σ el,1 (E) and σ el,2 (E). penelope reads these functions
from a precalculated database for electrons and positrons, for the elements Z = 1–92
and for a grid of energies that is dense enough to permit accurate cubic spline loglog
interpolation. This elastic scattering database was generated by using the partialwave
code of Salvat (2000); the atomic electron densities were obtained from the Dirac-
Hartree-Fock code of Desclaux (1975), which correspond to free atoms. Before starting
the simulation, penelope evaluates a table of the parameters A and B, and stores it in
the computer memory. Instead of B, penelope tabulates the quantity B ′ = +B (case
I) and B ′ = −B (case II); this avoids the need to specify the case, which can be inferred
from the sign of B ′ . It is worth noting that A and B ′ are continuous functions of energy
and, therefore, can be rapidly evaluated, for any energy, by interpolation in the stored
table. In case I, 〈µ〉 concides with 〈µ〉 W,A , which is determined by A, eq. (3.22). Fig.
3.5 displays the MW model parameters for aluminium and gold, as representative of
low- and high-Z elements. Notice that at high energies, where the case I model applies,
the strength of the delta contribution increases rapidly with energy, indicating that the
partial-wave DCS is much narrower than the Wentzel distribution.
The MW model is directly applicable to compounds (and mixtures) by using the