PERCOLATION AND DISORDERED SYSTEMS Geoffrey GRIMMETT

More documents

Recommendations

Info

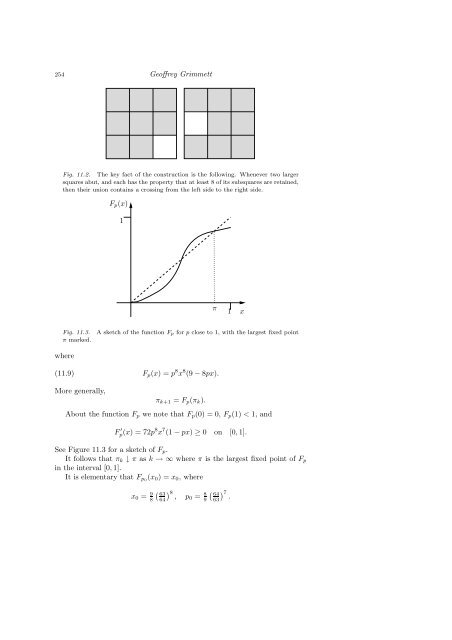
254 <strong>Geoffrey</strong> Grimmett Fig. 11.2. The key fact of the construction is the following. Whenever two larger squares abut, and each has the property that at least 8 of its subsquares are retained, then their union contains a crossing from the left side to the right side. Fp(x) 1 π 1 x Fig. 11.3. A sketch of the function Fp for p close to 1, with the largest fixed point π marked. where (11.9) Fp(x) = p 8 x 8 (9 − 8px). More generally, πk+1 = Fp(πk). About the function Fp we note that Fp(0) = 0, Fp(1) < 1, and F ′ p (x) = 72p8 x 7 (1 − px) ≥ 0 on [0, 1]. See Figure 11.3 for a sketch of Fp. It follows that πk ↓ π as k → ∞ where π is the largest fixed point of Fp in the interval [0, 1]. It is elementary that Fp0(x0) = x0, where x0 = 9 8 � � 63 8 64 , p0 = 8 9 � � 64 7 63 .
Percolation and Disordered Systems 255 It follows that π(p0) ≥ x0, yielding θ(p0) > 0. Therefore pc ≤ p0, as required in (11.5). The proof that θ(pc) > 0 is more delicate; see [113]. � Consider now the more general setting in which the random step involves replacing a typical square of side-length M −k by a M ×M grid of subsquares of common side-length M −(k+1) (the above concerns the case M = 3). For general M, a version of the above argument yields that the corresponding critical probability pc(M) satisfies pc(M) ≥ M −2 and also (11.10) pc(M) < 1 if M ≥ 3. When M = 2, we need a special argument in order to obtain that pc(2) < 1, and this may be achieved by using the following coupling of the cases M = 2 and M = 4 (see [91, 113]). Divide C0 into a 4 × 4 grid and do as follows. At the first stage, with probability p we retain all four squares in the top left corner; we do similarly for the three batches of four squares in each of the other three corners of C0. Now for the second stage: examine each subsquare of side-length 1 4 so far retained, and delete such a subsquare with probability p (different subsquares being treated independently). Note that the probability measure at the first stage dominates (stochastically) product measure with intensity π so long as (1−π) 4 ≥ 1−p. Choose π to satisfy equality here. The composite construction outlined above dominates (stochastically) a single step of a 4 × 4 random fractal with parameter pπ = p � 1 − (1 − p) 1 � 4 , which implies that and therefore pc(2) < 1 by (11.10). 11.3 A Morphology pc(2) � 1 − (1 − pc(2)) 1 � 4 ≤ pc(4) Random fractals have many phases, of which the existence of left-right crossings characterises only one. A weaker property than the existence of crossings is that the projection of C onto the x-axis is the whole interval [0, 1]. Projections of random fractals are of independent interest (see, for example, the ‘digital sundial’ theorem of [131]). Dekking and Meester [113] have cast such properties within a more general morphology. We write C for a random fractal in [0, 1] 2 (such as that presented in Section 11.1). The projection of C is denoted as πC = {x ∈ R : (x, y) ∈ C for some y}, and λ denotes Lebesgue measure. We say that C lies in one of the following phases if it has the stated property. A set is said to percolate if it contains a left-right crossing of [0, 1] 2 ; dimension is denoted by ‘dim’. I. C = ∅ a.s.
Page 1:
PERCOLATION AND DISORDERED SYSTEMS
Page 4 and 5:
144 Geoffrey Grimmett ÈÊÇ��
Page 6 and 7:
146 Geoffrey Grimmett 8. Critical P
Page 8 and 9:
148 Geoffrey Grimmett θ(p) 1 pc 1
Page 10 and 11:
150 Geoffrey Grimmett physical imag
Page 12 and 13:
152 Geoffrey Grimmett Fig. 2.1. Par
Page 14 and 15:
154 Geoffrey Grimmett Fig. 2.2. An
Page 16 and 17:
156 Geoffrey Grimmett 3.1 Percolati
Page 18 and 19:
158 Geoffrey Grimmett Kesten [201]
Page 20 and 21:
160 Geoffrey Grimmett whence d dp P
Page 22 and 23:
162 Geoffrey Grimmett Fig. 4.1. An
Page 24 and 25:
164 Geoffrey Grimmett s 1 θ = 0 pc
Page 26 and 27:
166 Geoffrey Grimmett ∂B(n) 0 e f
Page 28 and 29:
168 Geoffrey Grimmett Fig. 4.5. A s
Page 30 and 31:
170 Geoffrey Grimmett Theorem 5.5 (
Page 32 and 33:
172 Geoffrey Grimmett Proof of Theo
Page 34 and 35:
174 Geoffrey Grimmett 5.3 Site and
Page 36 and 37:
176 Geoffrey Grimmett 6.1 Using Sub
Page 38 and 39:
178 Geoffrey Grimmett Now φ(p) = 0
Page 40 and 41:
180 Geoffrey Grimmett so that (3.10
Page 42 and 43:
182 Geoffrey Grimmett x 2 y 2 x 4 x
Page 44 and 45:
184 Geoffrey Grimmett Similarly, Pp
Page 46 and 47:
186 Geoffrey Grimmett It remains to
Page 48 and 49:
188 Geoffrey Grimmett Fix β < pc a
Page 50 and 51:
190 Geoffrey Grimmett where δ 2 =
Page 52 and 53:
192 Geoffrey Grimmett Fig. 7.1. Tak
Page 54 and 55:
194 Geoffrey Grimmett 7.2 Percolati
Page 56 and 57:
196 Geoffrey Grimmett 4. The open c
Page 58 and 59:
198 Geoffrey Grimmett For n > m, le
Page 60 and 61:
200 Geoffrey Grimmett Lemma 7.17. I
Page 62 and 63:
202 Geoffrey Grimmett Lemma 7.24. S
Page 64 and 65: 204 Geoffrey Grimmett 000 111 000 1
Page 66 and 67: 206 Geoffrey Grimmett Fig. 7.7. An
Page 68 and 69: 208 Geoffrey Grimmett Fig. 7.9. The
Page 70 and 71: 210 Geoffrey Grimmett Fig. 7.10. Il
Page 72 and 73: 212 Geoffrey Grimmett 8.1 Percolati
Page 74 and 75: 214 Geoffrey Grimmett may be shown
Page 76 and 77: 216 Geoffrey Grimmett Lemma 8.11. L
Page 78 and 79: 218 Geoffrey Grimmett 0 u noting th
Page 80 and 81: 220 Geoffrey Grimmett where α ′
Page 82 and 83: 222 Geoffrey Grimmett The infra-red
Page 84 and 85: 224 Geoffrey Grimmett 9. PERCOLATIO
Page 86 and 87: 226 Geoffrey Grimmett Fig. 9.2. If
Page 88 and 89: 228 Geoffrey Grimmett x Fig. 9.3. I
Page 90 and 91: 230 Geoffrey Grimmett for crossing
Page 92 and 93: 232 Geoffrey Grimmett 10. RANDOM WA
Page 94 and 95: 234 Geoffrey Grimmett the volume of
Page 96 and 97: 236 Geoffrey Grimmett We define sim
Page 98 and 99: 238 Geoffrey Grimmett We now use th
Page 100 and 101: 240 Geoffrey Grimmett p+ 1 pc(site)
Page 102 and 103: 242 Geoffrey Grimmett Fig. 10.6. Th
Page 106 and 107: 246 Geoffrey Grimmett A L d -path i
Page 108 and 109: 248 Geoffrey Grimmett where pc(site
Page 110 and 111: 250 Geoffrey Grimmett now make two
Page 116 and 117: 256 Geoffrey Grimmett II. P(C �=
Page 118 and 119: 258 Geoffrey Grimmett Theorem 11.13
Page 120 and 121: 260 Geoffrey Grimmett (b) Under wha
Page 122 and 123: 262 Geoffrey Grimmett is obtained b
Page 124 and 125: 264 Geoffrey Grimmett 13.2 Weak Lim
Page 126 and 127: 266 Geoffrey Grimmett where p = 1
Page 128 and 129: 268 Geoffrey Grimmett Evidently pg(
Page 130 and 131: 270 Geoffrey Grimmett That is to sa
Page 132 and 133: 272 Geoffrey Grimmett which, via Le
Page 134 and 135: 274 Geoffrey Grimmett Turning to th
Page 136 and 137: 276 Geoffrey Grimmett Each circuit
Page 138 and 139: 278 Geoffrey Grimmett If A(q) < 1 (
Page 140 and 141: 280 Geoffrey Grimmett REFERENCES 1.
Page 142 and 143: 282 Geoffrey Grimmett 30. Alexander
Page 144 and 145: 284 Geoffrey Grimmett 63. Berg, J.
Page 146 and 147: 286 Geoffrey Grimmett 93. Chayes, J
Page 148 and 149: 288 Geoffrey Grimmett 123. Durrett,
Page 150 and 151: 290 Geoffrey Grimmett 158. Grimmett
Page 152 and 153: 292 Geoffrey Grimmett 191. Higuchi,
Page 154 and 155: 294 Geoffrey Grimmett 224. Koteck´
Page 156 and 157: 296 Geoffrey Grimmett 259. Meester,
Page 158 and 159: 298 Geoffrey Grimmett 290. Newman,
Page 160 and 161: 300 Geoffrey Grimmett 323. Roy, R.
Page 162 and 163: 302 Geoffrey Grimmett 355. Wierman,
show all

PERCOLATION AND DISORDERED SYSTEMS Geoffrey GRIMMETT

Create successful ePaper yourself

Delete template?

Save as template?